Skip to content

Latest commit

 

History

History
233 lines (184 loc) · 8.02 KB

2493.md

File metadata and controls

233 lines (184 loc) · 8.02 KB
title description keywords
2493. 将节点分成尽可能多的组
LeetCode 2493. 将节点分成尽可能多的组题解，Divide Nodes Into the Maximum Number of Groups，包含解题思路、复杂度分析以及完整的 JavaScript 代码实现。
LeetCode
2493. 将节点分成尽可能多的组
将节点分成尽可能多的组
Divide Nodes Into the Maximum Number of Groups
解题思路
广度优先搜索
并查集
图

2493. 将节点分成尽可能多的组

🔴 Hard  🔖  广度优先搜索 并查集 图  🔗 力扣 LeetCode

题目

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

  • Each node in the graph belongs to exactly one group.
  • For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximumm ) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1:

Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]

Output: 4

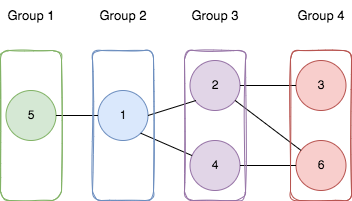
Explanation: As shown in the image we:

  • Add node 5 to the first group.
  • Add node 1 to the second group.
  • Add nodes 2 and 4 to the third group.
  • Add nodes 3 and 6 to the fourth group.

We can see that every edge is satisfied.

It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]

Output: -1

Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.

It can be shown that no grouping is possible.

Constraints:

  • 1 <= n <= 500
  • 1 <= edges.length <= 10^4
  • edges[i].length == 2
  • 1 <= ai, bi <= n
  • ai != bi
  • There is at most one edge between any pair of vertices.

题目大意

给你一个正整数 n ，表示一个 无向 图中的节点数目，节点编号从 1 到 n 。

同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 双向 边。注意给定的图可能是不连通的。

请你将图划分为 m 个组（编号从 1 开始），满足以下要求：

  • 图中每个节点都只属于一个组。
  • 图中每条边连接的两个点 [ai, bi] ，如果 ai 属于编号为 x 的组，bi 属于编号为 y 的组，那么 |y - x| = 1 。

请你返回最多可以将节点分为多少个组（也就是最大的 m ）。如果没办法在给定条件下分组，请你返回 -1 。

示例 1：

输入： n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]

输出： 4

解释： 如上图所示，

  • 节点 5 在第一个组。
  • 节点 1 在第二个组。
  • 节点 2 和节点 4 在第三个组。
  • 节点 3 和节点 6 在第四个组。

所有边都满足题目要求。

如果我们创建第五个组，将第三个组或者第四个组中任何一个节点放到第五个组，至少有一条边连接的两个节点所属的组编号不符合题目要求。

示例 2：

输入： n = 3, edges = [[1,2],[2,3],[3,1]]

输出： -1

解释： 如果我们将节点 1 放入第一个组，节点 2 放入第二个组，节点 3 放入第三个组，前两条边满足题目要求，但第三条边不满足题目要求。

没有任何符合题目要求的分组方式。

提示：

  • 1 <= n <= 500
  • 1 <= edges.length <= 10^4
  • edges[i].length == 2
  • 1 <= ai, bi <= n
  • ai != bi
  • 两个点之间至多只有一条边。

解题思路

  1. 构建邻接表：
    使用邻接表存储图结构，方便快速遍历邻居节点。

  2. BFS 检测奇环：

    • 使用 BFS 遍历每个连通分量，记录节点到根节点的深度。
    • 如果遍历过程中发现 相邻节点深度之差为奇数，说明存在奇数环，不符合要求，直接返回 -1。

  3. 计算最大组数：

    • 对于每个连通分量，选取不同的起点进行 BFS，记录最大深度。
    • 连通分量的最大深度即为当前分量的组数，累加到结果中。

  4. 返回结果：
    输出所有连通分量的最大可能分组数量。

复杂度分析

  • 时间复杂度：O(n + m)，其中 n 为节点数，m 为边数。构建邻接表 + 遍历所有连通分量 + BFS 检查节点。
  • 空间复杂度：O(n + m)，存储邻接表、访问标记和节点深度。

代码

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number}
 */
var magnificentSets = function (n, edges) {
	// 构建邻接表
	const graph = Array.from({ length: n + 1 }, () => []);
	for (const [u, v] of edges) {
		graph[u].push(v);
		graph[v].push(u);
	}

	const visited = Array(n + 1).fill(false);
	let maxGroups = 0;

	// BFS 检查是否有奇环，同时计算深度
	const bfs = (start) => {
		const queue = [[start, 1]];
		const nodeDepths = new Map();
		let maxDepth = 1;

		while (queue.length) {
			const [node, depth] = queue.shift();
			if (nodeDepths.has(node)) {
				if ((nodeDepths.get(node) - depth) % 2 !== 0) return -1; // 奇环
				continue;
			}
			nodeDepths.set(node, depth);
			maxDepth = Math.max(maxDepth, depth);

			for (const neighbor of graph[node]) {
				if (!nodeDepths.has(neighbor)) {
					queue.push([neighbor, depth + 1]);
				}
			}
		}
		return maxDepth;
	};

	// 遍历所有连通分量
	for (let i = 1; i <= n; i++) {
		if (!visited[i]) {
			const componentNodes = [];
			const queue = [i];
			visited[i] = true;

			// 获取连通分量中的所有节点
			while (queue.length) {
				const node = queue.shift();
				componentNodes.push(node);
				for (const neighbor of graph[node]) {
					if (!visited[neighbor]) {
						visited[neighbor] = true;
						queue.push(neighbor);
					}
				}
			}

			let bestDepth = 0;
			for (const node of componentNodes) {
				const depth = bfs(node);
				if (depth === -1) return -1;
				bestDepth = Math.max(bestDepth, depth);
			}
			maxGroups += bestDepth;
		}
	}

	return maxGroups;
};

相关题目

题号 标题 题解 标签 难度 力扣
102 二叉树的层序遍历 [✓] 树 广度优先搜索 二叉树 🟠 🀄️ 🔗
785 判断二分图 深度优先搜索 广度优先搜索 并查集 1+ 🟠 🀄️ 🔗
2608 图中的最短环 广度优先搜索 图 🔴 🀄️ 🔗