Arrays

This section covers ways in which to input and build arrays. Programming in Accelerate corresponds to expressing collective operations on arrays of type Array sh e. The Array type has two type parameters; sh is the shape of the array, the number and extent of each dimension; and e to represent the element type of the array.

Array types

Accelerate supports as array elements only simple atomic types, and tuples thereof. These element types can be stored efficiently in memory as consecutive memory slots without pointers. This feature is important to support backend implementations on exotic hardware, such as accelerate-cuda.

The supported array element types are members of the Elt class, including:

• ()
• Shapes and array indices
• Int, Int8, Int16, Int32, Int64
• Word, Word8, Word16, Word32, Word64
• Float
• Double
• Char
• Bool
• Tuple types up to 9-tuples, where the elements themselves are in Elt (this includes nested tuples)

Note that Array itself is not an allowable element type. There are no nested arrays in Accelerate, regular arrays only!

Getting data in

Converting from lists

You can create Accelerate arrays in many ways, for example, from a regular Haskell list using the following function:

fromList :: (Shape sh, Elt e) => sh -> [e] -> Array sh e

This will generate a multidimensional array by consuming elements from the list and adding them to the array in row-major order --- that is, the right-most index of the Shape type will change most rapidly.

Let us try that. Start ghci and import the module Data.Array.Accelerate.

ghci> fromList (Z:.10) [1..10]

<interactive>:0:1:
    No instance for (Shape (Z :. head0))
      arising from a use of `fromList'
    Possible fix: add an instance declaration for (Shape (Z :. head0))
    In the expression: fromList (Z :. 10) [0 .. ]
    In an equation for `it': it = fromList (Z :. 10) [0 .. ]

Oh no! The problem is that Shape is not a standard class, so defaulting does not apply. We can fix this by adding an explicit type signature to our array, as it can not be deduced from the surrounding context.

ghci> fromList (Z:.10) [0..] :: Vector Float
Array (Z :. 10) [0.0,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0]

Accelerate will often attempt to intimidate you with scary type errors, but persist and you shall be rewarded.

Okay, so we have made a vector. We can also generate multidimensional arrays in this fashion, so let's try a matrix:

ghci> fromList (Z:.3:.5) [1..] :: Array DIM2 Int
Array (Z :. 3 :. 5) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]

This creates a two-dimensional array with three rows of five elements each, by filling elements from the list along the rightmost dimension of the shape first.

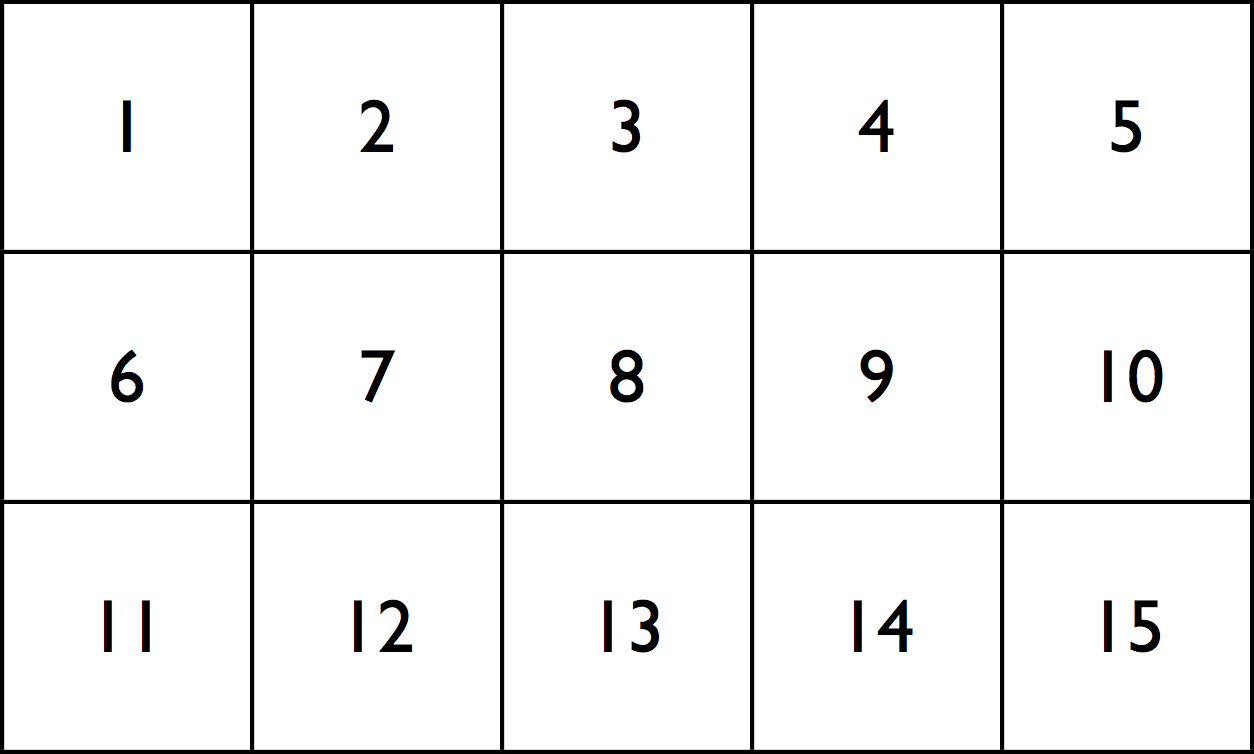
We can also index a specific element out of the array. Note that array indices start counting from zero!

ghci> let mat = fromList (Z:.3:.5) [1..] :: Array DIM2 Int
ghci> indexArray mat (Z:.2:.1)
12

We can even change the shape of an array without changing its representation. For example, change the 3x5 array above into a 5x3 array. This operation is part of the full Accelerate DSL, however, so we shall leave that until later.

Of course, internally the array is really just a vector, and the shape (Z :. 3 :. 5) tells Accelerate how to interpret the indices.

In a similar manner, we can create an array of, possibly nested, tuples.

ghci> fromList (Z:.2:.3) $ Prelude.zip [1..] ['a'..] :: Array DIM2 (Int,Char)
Array (Z :. 2 :. 3) [(1,'a'),(2,'b'),(3,'c'),(4,'d'),(5,'e'),(6,'f')]

Again, this is really just a trick; Accelerate is internally converting the array of tuples into a tuple of arrays.

Converting from Data.Array

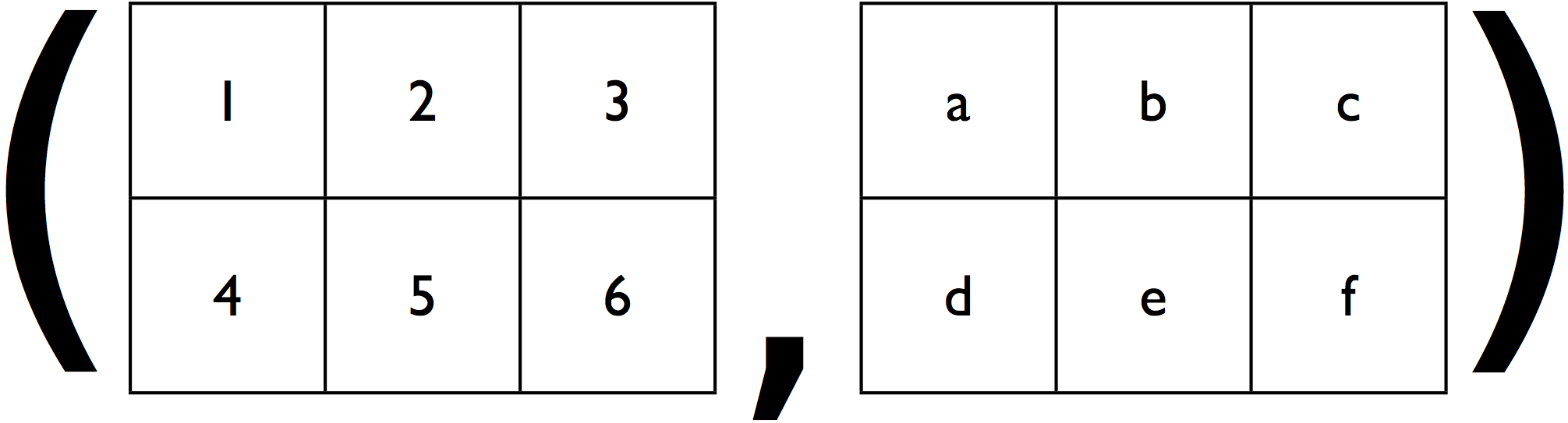
Similarly, we can convert immutable arrays defined by the Data.Array library (and friends) directly to Accelerate arrays using the following function:

fromIArray
  :: (IArray a e,
      Ix ix,
      Shape sh,
      Elt ix,
      Elt e,
      Data.Array.Accelerate.Array.Sugar.EltRepr ix
        ~
      Data.Array.Accelerate.Array.Sugar.EltRepr sh) =>
     a ix e -> A.Array sh e

This has a scary type signature, because it mentions some Accelerate internals that we can't get our hands on. Namely, the EltRepr type equality ensures that the dimensionality of the input IArray and output Accelerate array match.

In practice, satisfying this type signature is quite simple; the index type Ix of our input array must be an Int, or a tuple of Int's for multidimensional arrays. For singleton arrays, use index type `()'.

Lets start by declaring a vector of ten elements using the library Data.Array.Unboxed. Note that it is not necessary to use an unboxed array; we can just as easily convert from an IArray that uses boxed elements. The only requirement is that the array contain elements that are members of the Elt class, so that we know how to represent them in Accelerate.

ghci> let vec = listArray (0,9) [0..] :: UArray Int Float
ghci> vec
array (0,9) [(0,0.0),(1,1.0),(2,2.0),(3,3.0),(4,4.0),(5,5.0),(6,6.0),(7,7.0),(8,8.0),(9,9.0)]

Note that in contrast to Accelerate, the array library uses inclusive indexing, and that both the start and end of the range must be specified. We can then convert this into an Accelerate array using the fromIArray function.

ghci> fromIArary vec :: Vector Float
Array (Z :. 10) [0.0,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0]

Similarly, we can convert multidimensional arrays. For a two-dimensional Accelerate array, the index type of the IArray must be (Int,Int). For a three dimensional array, it would be (Int,Int,Int), and so forth.

ghci> let mat = listArray ((0,0), (1,4)) [1,1,1,1,1,2,2,2,2,2] :: UArray (Int,Int) Int
ghci> fromIArray mat :: Array DIM2 Int
Array (Z :. 2 :. 5) [1,1,1,1,1,2,2,2,2,2]

Similarly we can convert a singleton array, where the indexing type of the IArray is ().

ghci> let unit = listArray ((),()) [42] :: UArray () Int
ghci> fromIArray unit :: Scalar Int
Array Z [42]

Converting from Data.Vector

Convertiong from Data.Array.Repa

Impure arrays

On the Haskell side, arrays can be created and operated on in a mutable fashion, using destructive updates as in an imperative language. Once all operations are complete, the mutable array can be frozen and the pure immutable array lifted into Accelerate.

Mutable arrays combined with freezing are quite useful for initialising arrays using data from the outside world.

For example, to fill an array we:

• allocate an empty mutable IArray of size n
• destructively update the cells using a generator function
• freeze the IArray and convert to an Accelerate array

Here we initialise a mutable unboxed vector, fill it with randomly generated values, then convert the result into an Accelerate array.

{-# LANGUAGE BangPatterns, FlexibleContexts, ScopedTypeVariables #-}

import System.Random.MWC
import Data.Array.IO                            ( IOUArray )
import Data.Array.Unboxed                       ( IArray, UArray )
import Data.Array.MArray                        as M
import Data.Array.Accelerate                    as A

randoms
  :: forall e. (Variate e, Elt e, MArray IOUArray e IO, IArray UArray e)
  => GenIO
  -> Int
  -> IO (A.Array DIM1 e)
randoms gen n = do
  m     <- M.newArray_ (0,n-1)
  m'    <- fill m 0
  return $ A.fromIArray m'
  where
    fill :: IOUArray Int e -> Int -> IO (UArray Int e)
    fill !m !i
      | i < n     = do v <- uniform gen
                       M.writeArray m i v
                       fill m (i+1)
      | otherwise = M.unsafeFreeze m

Note that in this example you will want to compile with optimisations, otherwise unsafeFreeze will lead to stack overflow for large arrays.

Low-level conversions

TODO: using the accelerate-io package to read from pointers and ByteStrings.