Skip to content

Latest commit

 

History

History
429 lines (335 loc) · 12.7 KB

0122.买卖股票的最佳时机II.md

File metadata and controls

429 lines (335 loc) · 12.7 KB
Raw

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们受益！

122.买卖股票的最佳时机 II

力扣题目链接

给定一个数组，它的第  i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

  • 输入: [7,1,5,3,6,4]
  • 输出: 7
  • 解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

  • 输入: [1,2,3,4,5]
  • 输出: 4
  • 解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例  3:

  • 输入: [7,6,4,3,1]
  • 输出: 0
  • 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

  • 1 <= prices.length <= 3 * 10 ^ 4
  • 0 <= prices[i] <= 10 ^ 4

算法公开课

《代码随想录》算法视频公开课：贪心算法也能解决股票问题！LeetCode：122.买卖股票最佳时机 II，相信结合视频在看本篇题解，更有助于大家对本题的理解。

思路

本题首先要清楚两点：

  • 只有一只股票！
  • 当前只有买股票或者卖股票的操作

想获得利润至少要两天为一个交易单元。

贪心算法

这道题目可能我们只会想，选一个低的买入，再选个高的卖，再选一个低的买入.....循环反复。

如果想到其实最终利润是可以分解的，那么本题就很容易了！

如何分解呢？

假如第 0 天买入，第 3 天卖出，那么利润为：prices[3] - prices[0]。

相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

此时就是把利润分解为每天为单位的维度，而不是从 0 天到第 3 天整体去考虑！

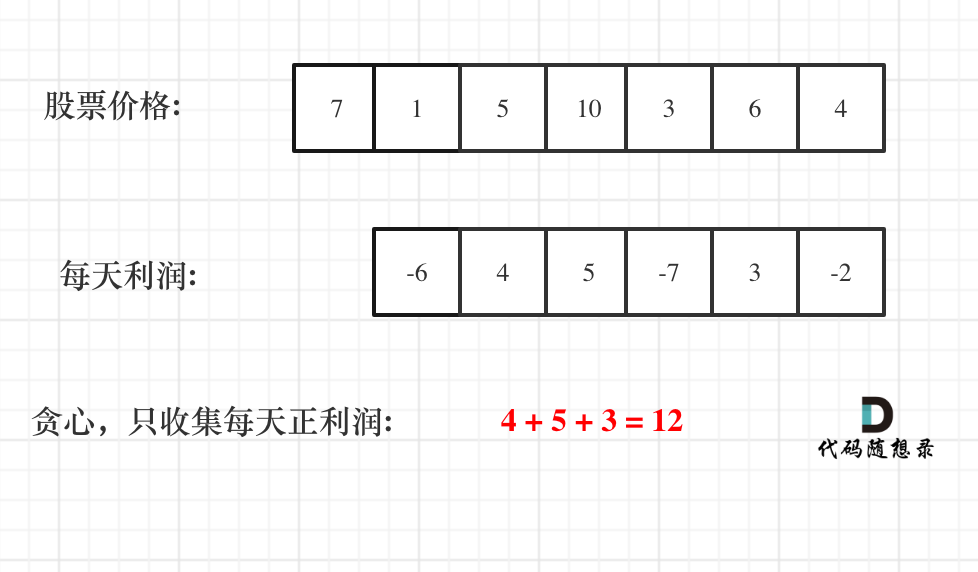
那么根据 prices 可以得到每天的利润序列：(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。

如图：

122.买卖股票的最佳时机II

一些同学陷入：第一天怎么就没有利润呢，第一天到底算不算的困惑中。

第一天当然没有利润，至少要第二天才会有利润，所以利润的序列比股票序列少一天！

从图中可以发现，其实我们需要收集每天的正利润就可以，收集正利润的区间，就是股票买卖的区间，而我们只需要关注最终利润，不需要记录区间。

那么只收集正利润就是贪心所贪的地方！

局部最优：收集每天的正利润，全局最优：求得最大利润。

局部最优可以推出全局最优，找不出反例，试一试贪心！

对应 C++代码如下：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result = 0;
        for (int i = 1; i < prices.size(); i++) {
            result += max(prices[i] - prices[i - 1], 0);
        }
        return result;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

动态规划

动态规划将在下一个系列详细讲解，本题解先给出我的 C++代码（带详细注释），想先学习的话，可以看本篇：122.买卖股票的最佳时机II（动态规划）

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        // dp[i][1]第i天持有的最多现金
        // dp[i][0]第i天持有股票后的最多现金
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(2, 0));
        dp[0][0] -= prices[0]; // 持股票
        for (int i = 1; i < n; i++) {
            // 第i天持股票所剩最多现金 = max(第i-1天持股票所剩现金, 第i-1天持现金-买第i天的股票)
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            // 第i天持有最多现金 = max(第i-1天持有的最多现金，第i-1天持有股票的最多现金+第i天卖出股票)
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return max(dp[n - 1][0], dp[n - 1][1]);
    }
};
  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

总结

股票问题其实是一个系列的，属于动态规划的范畴，因为目前在讲解贪心系列，所以股票问题会在之后的动态规划系列中详细讲解。

可以看出有时候，贪心往往比动态规划更巧妙，更好用，所以别小看了贪心算法。

本题中理解利润拆分是关键点！ 不要整块的去看，而是把整体利润拆为每天的利润。

一旦想到这里了，很自然就会想到贪心了，即：只收集每天的正利润，最后稳稳的就是最大利润了。

其他语言版本

Java:

贪心:

// 贪心思路
class Solution {
    public int maxProfit(int[] prices) {
        int result = 0;
        for (int i = 1; i < prices.length; i++) {
            result += Math.max(prices[i] - prices[i - 1], 0);
        }
        return result;
    }
}

动态规划:

class Solution { // 动态规划
    public int maxProfit(int[] prices) {
        // [天数][是否持有股票]
        int[][] dp = new int[prices.length][2];

        // base case
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        for (int i = 1; i < prices.length; i++) {
            // dp公式
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }

        return dp[prices.length - 1][0];
    }
}

Python:

贪心:

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        result = 0
        for i in range(1, len(prices)):
            result += max(prices[i] - prices[i - 1], 0)
        return result

动态规划:

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        dp = [[0] * 2 for _ in range(length)]
        dp[0][0] = -prices[0]
        dp[0][1] = 0
        for i in range(1, length):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]) #注意这里是和121. 买卖股票的最佳时机唯一不同的地方
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
        return dp[-1][1]

Go:

贪心算法

func maxProfit(prices []int) int {
    var sum int
    for i := 1; i < len(prices); i++ {
        // 累加每次大于0的交易
        if prices[i] - prices[i-1] > 0 {
            sum += prices[i] - prices[i-1]
        }
    }
    return sum
}

动态规划

func maxProfit(prices []int) int {
    dp := make([][]int, len(prices))
    for i := 0; i < len(dp); i++ {
        dp[i] = make([]int, 2)
    }
    // dp[i][0]表示在状态i不持有股票的现金，dp[i][1]为持有股票的现金
    dp[0][0], dp[0][1] = 0, -prices[0]
    for i := 1; i < len(prices); i++ {
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1])
    }
    return dp[len(prices)-1][0]

}
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

Javascript:

贪心

var maxProfit = function(prices) {
    let result = 0
    for(let i = 1; i < prices.length; i++) {
        result += Math.max(prices[i] - prices[i - 1], 0)
    }
    return result
};

动态规划

const maxProfit = (prices) => {
  let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
  // dp[i][0] 表示第i天持有股票所得现金。
  // dp[i][1] 表示第i天不持有股票所得最多现金
  dp[0][0] = 0 - prices[0];
  dp[0][1] = 0;
  for (let i = 1; i < prices.length; i++) {
    // 如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来
    // 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
    // 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);

    // 在来看看如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来
    // 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
    // 第i天卖出股票，所得现金就是按照今天股票佳价格卖出后所得现金即：prices[i] + dp[i - 1][0]
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
  }

  return dp[prices.length - 1][1];
};

TypeScript：

贪心

function maxProfit(prices: number[]): number {
  let resProfit: number = 0;
  for (let i = 1, length = prices.length; i < length; i++) {
    resProfit += Math.max(prices[i] - prices[i - 1], 0);
  }
  return resProfit;
}

动态规划

function maxProfit(prices: number[]): number {
  const dp = Array(prices.length)
    .fill(0)
    .map(() => Array(2).fill(0))
  dp[0][0] = -prices[0]
  for (let i = 1; i < prices.length; i++) {
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i])
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i])
  }
  return dp[prices.length - 1][1]
}

Rust：

贪心：

impl Solution {
    pub fn max_profit(prices: Vec<i32>) -> i32 {
        let mut result = 0;
        for i in 1..prices.len() {
            result += (prices[i] - prices[i - 1]).max(0);
        }
        result
    }
}

动态规划：

impl Solution {
    pub fn max_profit(prices: Vec<i32>) -> i32 {
        let mut dp = vec![vec![0; 2]; prices.len()];
        dp[0][0] = -prices[0];
        for i in 1..prices.len() {
            dp[i][0] = dp[i - 1][0].max(dp[i - 1][1] - prices[i]);
            dp[i][1] = dp[i - 1][1].max(dp[i - 1][0] + prices[i]);
        }
        dp[prices.len() - 1][1]
    }
}

C:

贪心：

int maxProfit(int* prices, int pricesSize){
    int result = 0;
    int i;
    //从第二个元素开始遍历数组，与之前的元素进行比较
    for(i = 1; i < pricesSize; ++i) {
        //若该元素比前面元素大，则说明有利润。代表买入
        if(prices[i] > prices[i-1])
            result+= prices[i]-prices[i-1];
    }
    return result;
}

动态规划：

#define max(a, b) (((a) > (b)) ? (a) : (b))

int maxProfit(int* prices, int pricesSize){
    int dp[pricesSize][2];
    dp[0][0] = 0 - prices[0];
    dp[0][1] = 0;

    int i;
    for(i = 1; i < pricesSize; ++i) {
        // dp[i][0]为i-1天持股的钱数/在第i天用i-1天的钱买入的最大值。
        // 若i-1天持股，且第i天买入股票比i-1天持股时更亏，说明应在i-1天时持股
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]);
        //dp[i][1]为i-1天不持股钱数/在第i天卖出所持股票dp[i-1][0] + prices[i]的最大值
        dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
    }
    // 返回在最后一天不持股时的钱数（将股票卖出后钱最大化）
    return dp[pricesSize - 1][1];
}

Scala：

贪心:

object Solution {
  def maxProfit(prices: Array[Int]): Int = {
    var result = 0
    for (i <- 1 until prices.length) {
      if (prices(i) > prices(i - 1)) {
        result += prices(i) - prices(i - 1)
      }
    }
    result
  }
}

C#

public class Solution
{
    public int MaxProfit(int[] prices)
    {
        int res = 0;
        for (int i = 0; i < prices.Length - 1; i++)
        {
            res += Math.Max(0, prices[i + 1] - prices[i]);
        }
        return res;
    }
}