Skip to content

Latest commit

 

History

History
233 lines (126 loc) · 13.9 KB

attention is all you need.md

File metadata and controls

233 lines (126 loc) · 13.9 KB
Raw

Attention Is All You Need

参考博客：https://www.cnblogs.com/nickchen121/p/16470569.html#%E5%8D%81transformer

这是一篇由Ashish Vaswani等人发表在Neural Information Processing Systems（NIPS）2017年会议上的自然语言处理（NLP）领域的论文。该论文主要介绍了Transformer模型。

Abstract

主要的序列转导模型是基于复杂的循环或卷积神经网络，包括一个编码器和一个解码器。表现最好的模型还通过注意力机制连接编码器和解码器。

一种新的简单网络架构：Transformer 完全基于注意力机制，摒弃了递归和卷积。更加并行化，需要更少的训练时间。

Transformer

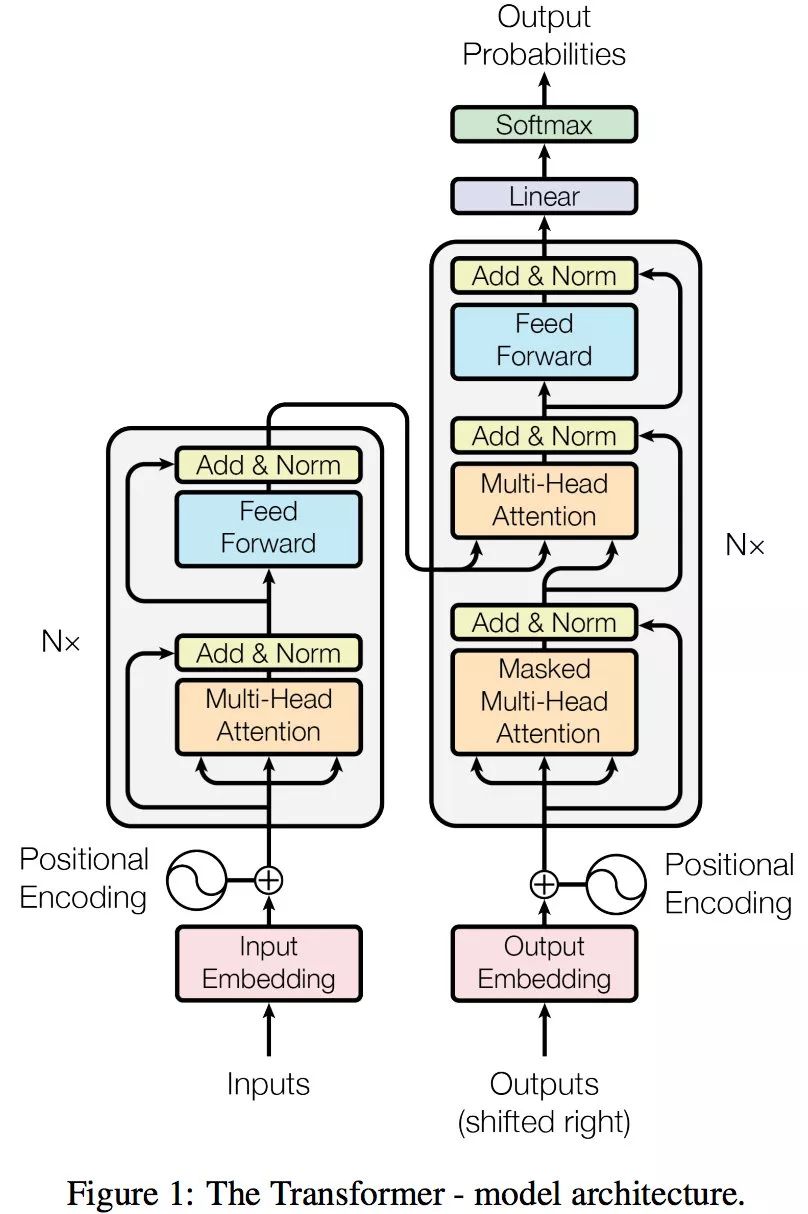
Transformer 的整体框架如下图所示：

img

上图所示的整体框架乍一眼一看非常复杂，再画张图直观的看就是这样：

img

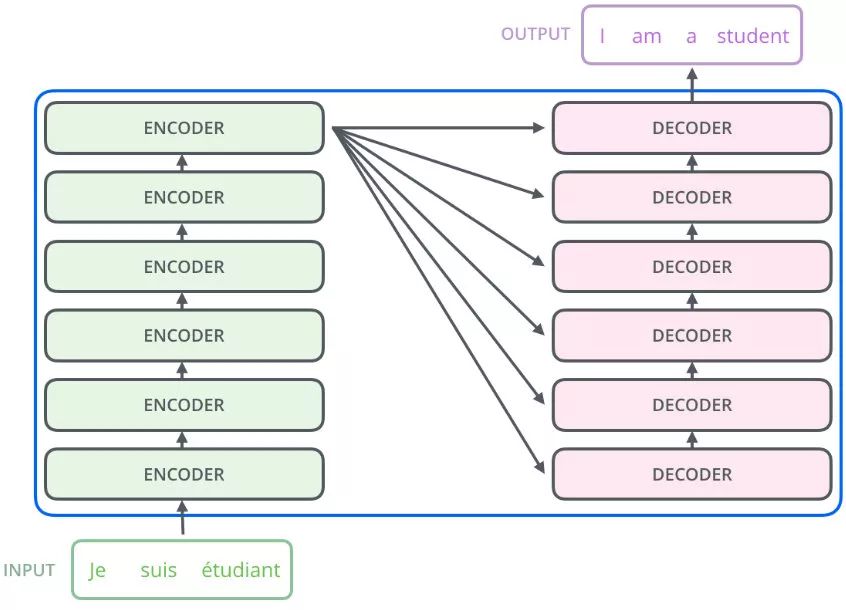
也就是说，Encoders 的输出，会和每一层的 Decoder 进行结合。

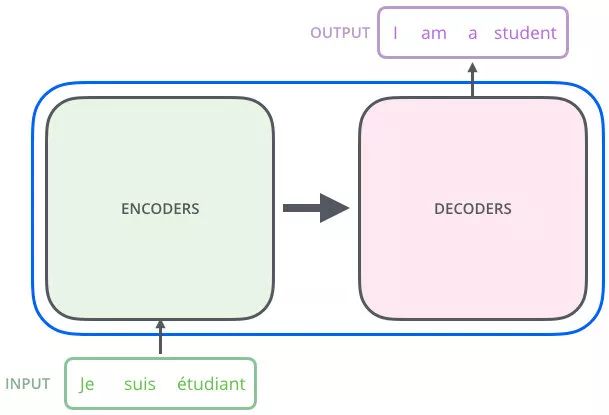
再简化一下，左边一个 Encoders 把输入读进去，右边一个 Decoders 得到输出，如下所示：

img

想要详细了解 Transformer，只要了解 Transformer 中的 Encoder 和 Decoder 单元即可，接下来详细阐述这两个单元。

Encoder

每层 Encoder 包括 2 个 sub-layers：

  • 第一个 sub-layer 是 Multi-Head Attention，用来计算输入的词向量；
  • 第二个 sub-layer 是简单的前馈神经网络层 Feed Forward；

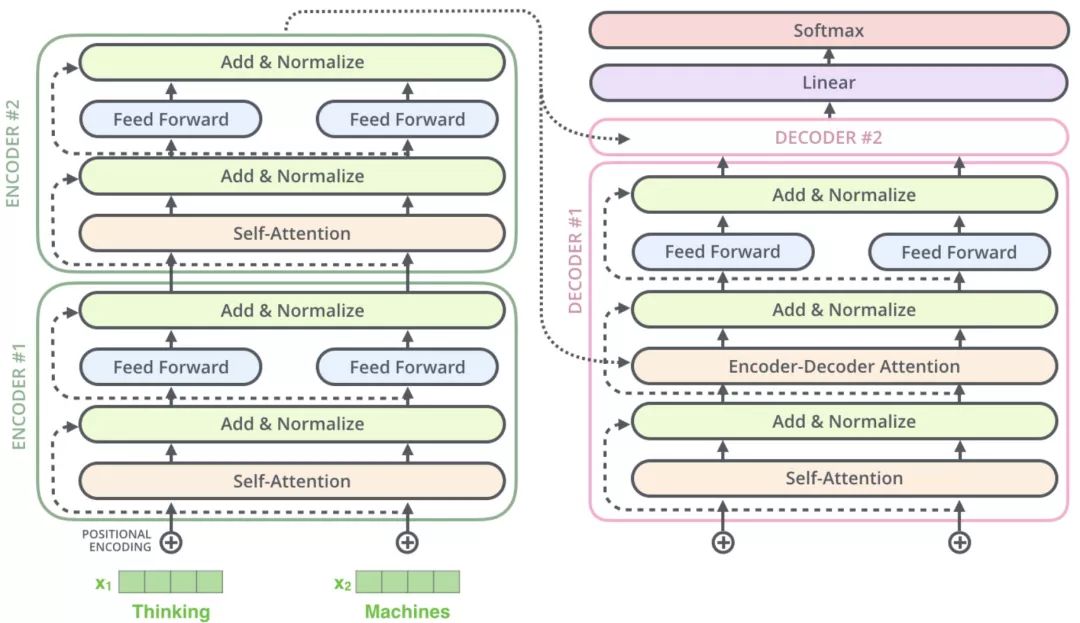
现在我们给出 Encoder 的数据流示意图，一步一步去剖析

img

  1. 深绿色的 $x_1$ 表示 Embedding 层的输出，经过[Positional Encoding](# Positional Encoding)，加上代表 Positional Embedding 的向量之后，得到最后输入 Encoder 中的特征向量，也就是浅绿色向量 $x_1$；

  2. 浅绿色向量 $x_1$ 表示单词 “Thinking” 的特征向量，其中 $x_1$ 经过 Self-Attention 层，变成浅粉色向量 $z_1$ ；

  3. $x_1$ 作为残差结构的直连向量，直接和$z_1$相加，之后进行 $LayerNorm$ 操作，得到粉色向量 $z_1$ ；

  • 残差结构 Add 的作用：避免出现梯度消失的情况

  • Normalize 的作用：归一化，为了保证数据特征分布的稳定性，并且可以加速模型的收敛

  1. $z_1$ 经过前馈神经网络 Feed Forward 层，经过残差结构与自身相加，之后经过 Layer Norm 层，得到一个输出向量 $r_1$ ；
  • 该前馈神经网络包括两个线性变换和一个 $Relu$ 激活函数：$FFN(x) = max(0,xW_1+b_1)W_2+b2$
  1. 由于 Transformer 的 Encoders 具有 6 个 Encoder，$r_1$ 也将会作为下一层 Encoder 的输入，代替 $x_1$ 的角色，如此循环，直至最后一层 Encoder。

需要注意的是，上述的 $x、z、r$ 都具有相同的维数 dmodel，论文中为 512 维。

==总结==：输入一个词向量，经过 Positional Encoding 获得位置信息， 然后通过 Self-Attention 得到语义信息和句法信息， 再通过 Feed Forward 做一次非线性变换拟合空间中任意一种状态，过程中使用残差结构和归一化 Add&Normalize 避免梯度消失和梯度爆炸，最后输出一个更好的词向量。

Decoder

每层 Decoder 包括 3 个 sub-layers：

  • 第一个 sub-layer 是 Masked Multi-Head Attention，也是计算输入的词向量；
  • 第二个 sub-layer 是 Encoder-Decoder Attention 计算，对 Encoder 的输入和 Decoder 第一个子层的输出进行 attention 计算；
  • 第三个 sub-layer 是前馈神经网络 Feed Forward 层，与 Encoder 相同。

img

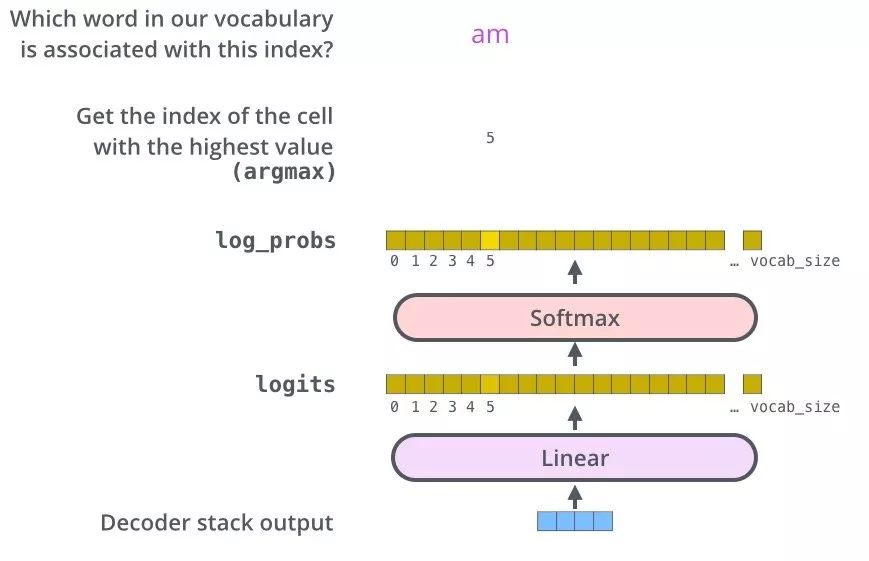
从上图可以看出，Transformer 最后的工作是让解码器的输出通过线性层 Linear 后接上一个 Softmax

  • Linear 层是一个简单的全连接神经网络，它将解码器产生的向量 A 投影到一个更高维度的向量 B 上，假设我们模型的词汇表是10000个词，那么向量 B 就有10000个维度，每个维度对应一个唯一的词的得分。
  • Softmax 层将这些分数转换为概率。选择概率最大的维度，并对应地生成与之关联的单词

img

Attention

Scaled Dot-Product Attention

注意力模型 Attention 的本质思想为：从大量信息中有选择地筛选出少量重要信息并聚焦到这些重要信息上，忽略不重要的信息。

Attention 机制可以更加好的解决序列长距离依赖问题，并且具有并行计算能力。

注意力模型从大量信息 Values 中筛选出少量重要信息，这些重要信息一定是相对于另外一个信息 Query 而言是重要的。也就是说，我们要搭建一个注意力模型，我们必须得要有一个 Query 和一个 Values，然后通过 Query 这个信息从 Values 中筛选出重要信息。

通过 Query 这个信息从 Values 中筛选出重要信息，简单点说，就是计算 Query 和 Values 中每个信息的相关程度。

img

通过上图，Attention 通常可以进行如下描述，表示为将 Query(Q) 和 key-value pairs（把 Values 拆分成了键值对的形式） 映射到输出上，其中 Query、每个 Key、每个 Value 都是向量，输出是 V 中所有 Values 的加权，其中权重是由 Query 和每个 Key 计算出来的，计算方法分为三步：

  1. 第一步：计算比较 Q 和 K 的相似度，用 f 来表示： $f(Q,K_i)$ $i=1,2,⋯,m$ 一般第一步计算方法包括四种：
    • 点乘（Transformer 使用）： $f(Q,K_i)=Q^TK_i$
    • 权重：$f(Q,K_i)=Q^TWK_i$
    • 拼接权重：$f(Q,K_i)=W[Q^T;K_i]$
    • 感知器：$f(Q,K_i)=V^Ttanh(WQ+UK_i)$
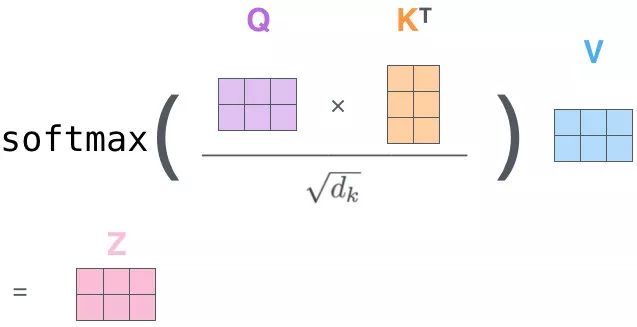
  2. 第二步：将得到的相似度进行 softmax 操作，进行归一化：$α_i=softmax(\frac{f(Q,K_i)}{\sqrt{d_k}})$
  3. 第三步：针对计算出来的权重 $α_i$，对 V 中的所有 Values 进行加权求和计算，得到 Attention 向量：==$Attention=\sum_{i=1}^{m} α_iV_i$==

Self Attention

Self Attention 模型的架构如下图所示：

img

首先可以看到 Self Attention 有三个输入 Q、K、V：对于 Self Attention，Q、K、V 来自句子 X 的 词向量 x 的线性转化，即对于词向量 x，给定三个可学习的矩阵参数 $W_Q,W_K,W_V$ ，x 分别右乘上述矩阵得到 Q、K、V。

接下来先通过向量的计算叙述 Self Attention 计算的流程，然后再描述 Self Attention 的矩阵计算过程

向量计算流程

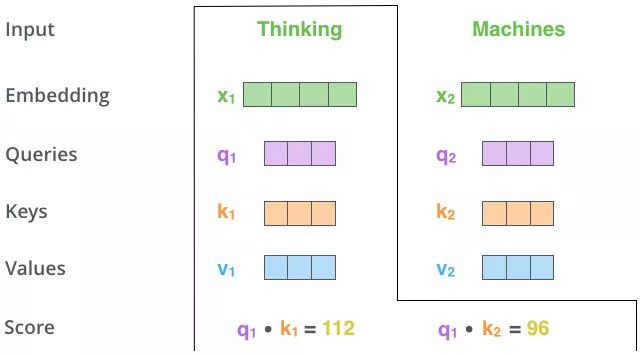
第一步，Q、K、V 的获取

img

上图操作：两个单词 Thinking 和 Machines。通过线性变换，即 $x_1$ 和 $x_2$ 两个向量分别与 $W_Q,W_K,W_V$ 三个矩阵点乘得到 $q_1,q_2,k_1,k_2,v_1,v_2$ 共 6 个向量。矩阵 Q 则是向量 $q_1,q_2$ 的拼接，K、V 同理。

第二步，MatMul

img

上图操作：向量 $q_1,k_1$ 做点乘得到得分 112， $q_1,k_2$ 做点乘得到得分96。注意：这里是通过 $q_1$ 这个信息找到 $x_1,x_2$ 中的重要信息。

第三步和第四步，Scale + Softmax

img

第五步，MatMul

img

用得分比例 [0.88，0.12] 乘以 $v_1,v_2$ 值得到一个加权后的值，将这些值加起来得到 $z_1$。

上述所说就是 Self Attention 模型所做的事，仔细感受一下，用 $q_1、K=[k_1,k_2]$ 去计算一个x` Thinking 相对于 Thinking 和 Machine 的权重，再用权重乘以 Thinking 和 Machine 的 $V=[v_1,v_2]$ 得到加权后的 Thinking 和 Machine 的 $V'=[v_1',v_2']$，最后求和得到针对各单词的输出 $z_1$。

同理可以计算出 Machine 相对于 Thinking 和 Machine 的加权输出 $z_2$，拼接 $z_1,z_2$ 得到 Attention 值 $Z=[z_1,z_2]$，这就是 Self Attention 的矩阵计算。

矩阵计算流程

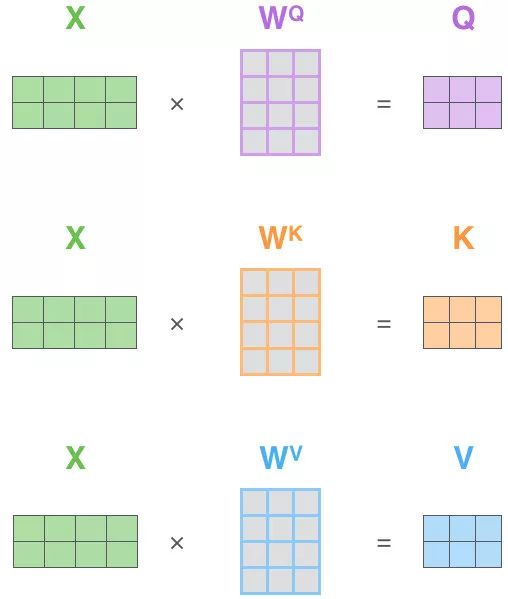
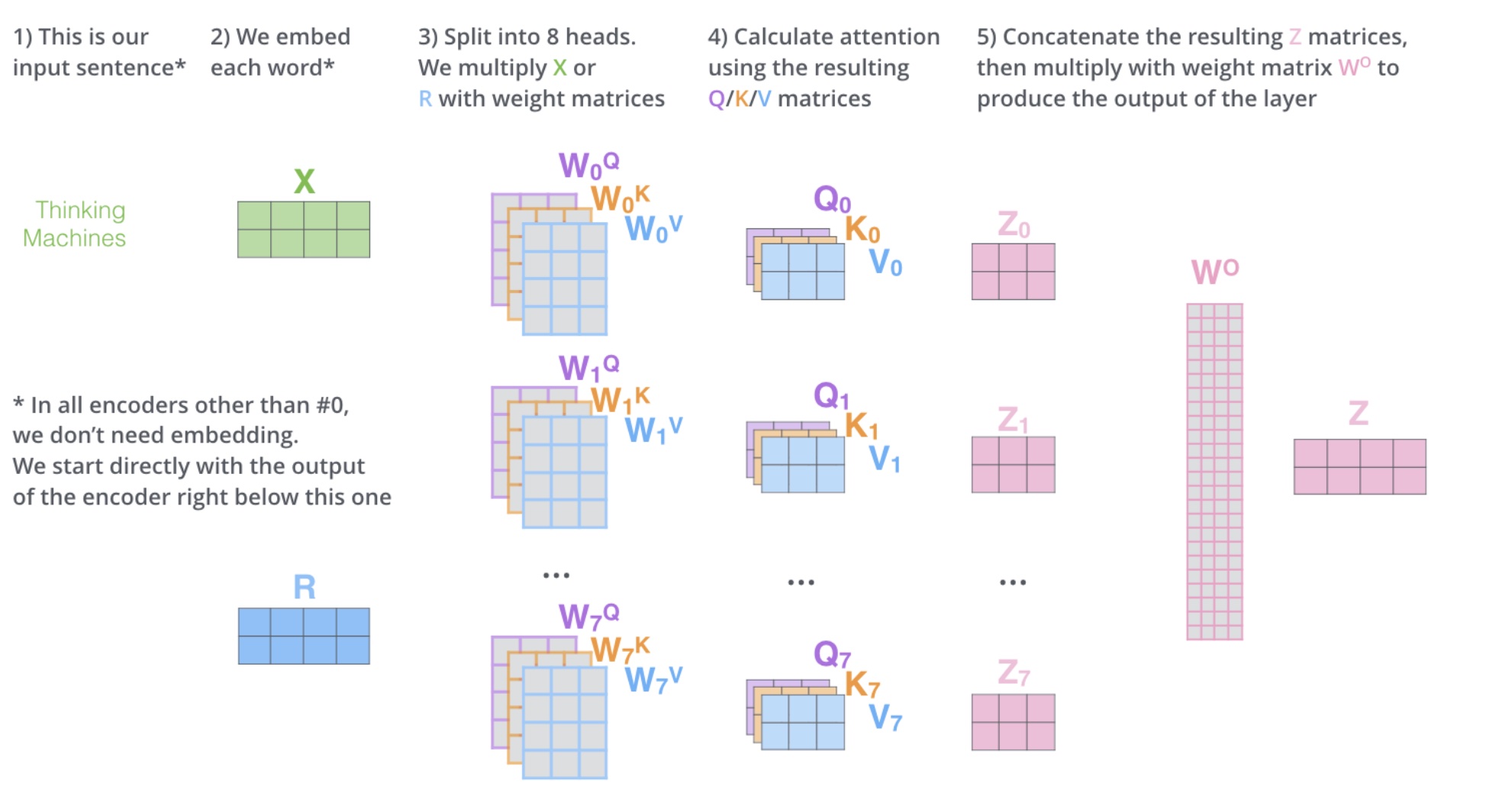
之前的例子是单个向量的运算例子。这张图展示的是矩阵运算的例子，输入是一个 [2x4] 的矩阵（句子中每个单词的词向量的拼接），每个运算是 [4x3] 的矩阵，求得 Q、K、V。

img

Q 对 $K^T$ 做点乘，除以 $\sqrt{dk}$，做一个 softmax 得到合为 1 的比例，对 V 做点乘得到输出 Z。那么这个 Z 就是一个考虑过 Thinking 周围单词 Machine 的输出。==$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$==

img

$QK^T$ 其实就会组成一个 attention map。如果输入是一句话 "i have a dream" 总共 4 个单词，这里就会形成一张 4x4 的注意力机制的图：

img

这样一来，每一个单词对应每一个单词都会有一个权重，这也是 Self Attention 名字的来源，即 Attention 的计算来源于 Source（源句） 和 Source 本身，通俗点讲就是 Q、K、V 都来源于输入 X 本身。

Multi-Head Attention

Multi-Head Attention 就是把 Self Attention 得到的注意力值 $Z$ 切分成 n 个 $Z_1,Z_2,⋯,Z_n$，然后通过全连接层获得新的 $Z'$.

img

对 $Z$ 进行 8 等份的切分得到 8 个 $Z_i$ 矩阵：

img

为了使得输出与输入结构相同，拼接矩阵 $Z_i$ 后乘以一个线性 $W^O$ 得到最终的 $Z$：

img

可以通过下图看看 multi-head attention 的整个流程：

img

多头相当于把原始信息 Source 放入了多个子空间中，也就是捕捉了多个信息，对于使用 multi-head（多头） attention 的简单回答就是，多头保证了 attention 可以注意到不同子空间的信息，捕捉到更加丰富的特征信息

Masked Multi-Head Attention

结构如下图所示：

img

假设在此之前已经得到了一个 attention map，而 mask 就是沿着对角线把灰色的区域用0覆盖掉，不给模型看到未来的信息，如下图所示：

img

详细来说：

  1. "i" 作为第一个单词，只能有和 "i" 自己的 attention；
  2. "have" 作为第二个单词，有和 "i、have" 前面两个单词的 attention；
  3. "a" 作为第三个单词，有和 "i、have、a" 前面三个单词的 attention；
  4. "dream" 作为最后一个单词，才有对整个句子 4 个单词的 attention。

为什么 Decoder 需要做 Mask

  • 训练阶段：我们知道 “我是学生” 的翻译结果为 “I am a student”，我们把 “I am a student” 的 Embedding 输入到 Decoders 里面，翻译第一个词 “I” 时
    • 如果对 “I am a student” attention 计算不做 mask，“am，a，student” 对 “I” 的翻译将会有一定的贡献
    • 如果对 “I am a student” attention 计算做 mask，“am，a，student” 对 “I” 的翻译将没有贡献
  • 测试阶段：我们不知道 “我爱中国” 的翻译结果为 “I love China”，我们只能随机初始化一个 Embedding 输入到 Decoders 里面，翻译第一个词 “I” 时：
    • 无论是否做 mask，“love，China” 对 “I” 的翻译都不会产生贡献
    • 但是翻译了第一个词 “I” 后，随机初始化的 Embedding 有了 “I” 的 Embedding，也就是说在翻译第二词 “love” 的时候，“I” 的 Embedding 将有一定的贡献，但是 “China” 对 “love” 的翻译毫无贡献，随之翻译的进行，已经翻译的结果将会对下一个要翻译的词都会有一定的贡献，这就和做了 mask 的训练阶段做到了一种匹配

总结下就是：Decoder 做 Mask，是为了让训练阶段和测试阶段行为一致，不会出现 gap ，避免过拟合

Positional Encoding

Self Attention 的 $Q、K、V$ 三个矩阵是由同一个输入 $X_1=(x_1,x_2,\cdots,x_n) $ 线性转换而来，也就是说对于这样的一个被打乱序列顺序的 $X_2=(x_2,x_1,\cdots,x_n) $ 而言，由于 attention 值的计算最终会被加权求和，也就是说两者最终计算的 attention 值都是一样的，进而也就表明了 attention 丢掉了 $X_1$ 的序列顺序信息。

img

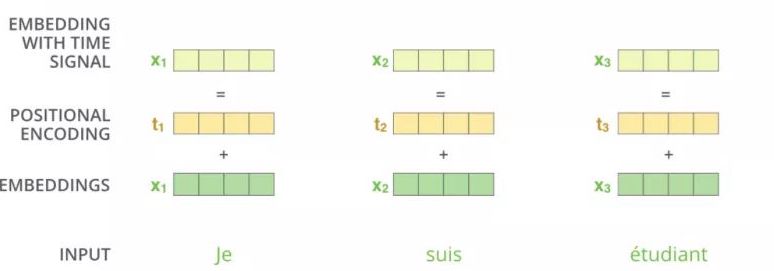
如上图所示，为了解决 Attention 丢失的序列顺序信息，Transformer 的提出者提出了 Position Embedding，也就是对于输入 $X$ 进行 Attention 计算之前，在 $X$ 的词向量中加上位置信息，也就是说 $X$ 的词向量为 $X_{final_embedding} = Embedding + Positional, Embedding$

其中位置编码公式如下所示：

$PE(pos,2i) = sin(pos/10000^{2i/d_{model}})$

$PE(pos,2i+1) = cos(pos/10000^{2i/d_{model}})$

Training Data

WMT 2014 English-German dataset