DataViz_2021.Rmd

---
title: "Data Visualization and Mixed Models"
author: "Limor Raviv"
date: "May 2021"
output:
  pdf_document: default
  html_document:
    df_print: paged
  word_document: default
---

```{r setup, include=FALSE}
# Basic settings (just trust me on this :P)
options(scipen = 99999) 
options(mc.cores=2) 
knitr::opts_chunk$set(echo = FALSE, warning = FALSE)
```

#Introduction
The following Rmarkdown document includes a detailed example of how to visualize data and plot regression models' output.

We'll use the "GSSvocab" dataset, which contains information from the General Social Survey (GSS) of the University of Chicago. It inlcudes vocabulary scores collected over the course of 20 years from over 28,000 people. We'll analyze the vocabulary scores by individuals' age, gender, education level and nativeness. 

Feel free to reuse and edit any part of this document/code!


# Reminder: What's Rmarkdown?
This is an R Markdown document. It basically combines text with R code (models, plots etc), and can be used to create beautiful HTMLs, PDFs, Word documents, slides and even websites. 

When you click on the "Knit" button on top, it will generate a  document that includes all the specified content: this text, as well as the output of any embedded R code chunks within the document (unless you decide not to include it in your final output).

For more details on using R Markdown see <http://rmarkdown.rstudio.com>. 

I also recommend using this awesome cheat sheet: <https://github.com/rstudio/cheatsheets/raw/master/rmarkdown-2.0.pdf>

## Text in Rmarkdown
Text appears like this, on a white background.

You can format the text to be **bold** or *italics*, and have it appear in different sizes by starting a line with hashtags:

# for main headers
## for subheaders
### for subsubheaders 

You can also use lists and bullet-points:

1. This 
2. is
3. a list

- and 
- these
- are
- bullets

And even write nice equations by using the dollar sign:
$$ \frac{n!}{k!(n-k)!} = \binom{n}{k} $$

## Code in Rmarkdown
Chuncks of code appear in a grey box denoted by ``` at the begining and end, and have a curly-brackets header (see below). The code always starts with some name, and then some technical instructions (e.g., do you want to include the actual code in the document or just the output? Do you want to see warnings?). For example "echo=TRUE" means I want the code itself to appear in the final file (not just an output, if any). Check out the cheat sheet for more details.

```{r exmaple code, echo=TRUE}

example <- 1.987

```

You can also include some R code inside the text by using `r "your code in grave accents" `. For exmaple, 2 multiplied by 10 equals `r 2*10`. This can be used to integrate values from your enviroment (like beta-coefficients) in the actual text without the need to copy them, like the value from the exmaple above is `r example`.



# Let's get started!
For editing and running the code, please install and load the following packages first.

*Note that "include=FALSE" here means that this chunk of code will not appear in  the final document.*

```{r general_setup, include=FALSE, warning=FALSE, cache=TRUE}

# Install the needed packages by uncommenting and running the code.
# Once you've run it, comment the code out again.

# TIP: use ctrl+shift+c for uncommenting/commenting a bunch of lines at once


# install.packages("markdown") # Rmarkdown packages
# install.packages("knitr") # adding nice tables
# install.packages("ggplot2") # making beautiful plots
# install.packages("effects") # plotting models
# install.packages("cowplot") # making paneled plots
# install.packages("plyr") # summarize data
# install.packages("dplyr") # summarize data
# install.packages("carData") # contains our data set
# install.packages("lme4") # regression models (you should already have this package)
# install.packages("gghighlight") # highlighying lines
# install.packages("tweenr") # animating plots
# install.packages("png") # animating plots
# install.packages("gifski") # animating plots
# install.packages("gganimate")  # animating plots
      ## this package causes trouble based upon versions of R.  if you can't install, it just means you won't be able to run 1 kind of plot-- don't stress about getting it installed.

# Load the needed packages
library(markdown)
library(knitr)
library(ggplot2) 
library(effects) 
library(cowplot) 
library(plyr) 
library(dplyr) 
library(carData)
library(lme4)
library(gghighlight)
library(gganimate)
library(gifski)
library(png)
library(tweenr)
```

## The dataset
Now, let's load the dataset and play with it a bit to see what's going on.

```{r load_data, echo=FALSE, cache=TRUE}

data("GSSvocab")

summary(GSSvocab) # look at the data

# Let's recode the variable "nativeborn"" to make the output more informative!

levels(GSSvocab$nativeBorn) <- c("Non-native", "Native") # This is better than "yes"/"no"

summary(GSSvocab)  ## re-summarise and look: levels of 'nativeBorn' are changed


# Notice that ageGroup and educGroup are a binned variable based on age and educ
# Since making continuous variables into categorical variables is not good practice (and also takes away from our model's power), we will not use them here.
# Thus, we don't need all this data-- we just want really the non-binned variables - so let's remove it. 

d<- GSSvocab[!is.na(GSSvocab$vocab),c(1:3,6:8)]  # Create a new data frame with only the wanted columns, remove all the lines where vocab score is n/a
# Note that we also gave the data frame a shorter name (more convenient)

```


### Predictions?

Before we look at the data, what are your predictions? What do you think will affect vocabulary scores?

**For each of these variables, write down: Do you think this variable matters? How so? Should it be a fixed effect or a random effect?**

- year (of data collection)
- gender
- nativeBorn (in the USA)
- age
- educ (years of formal education)

**Think: Do you expect any interactions?**

For example, it's possible that being native to the US will moderate the effect of education and/or age.
DO you think this relation will be further moderated by gender?



## Plotting the data

To examine our data, we can first plot it in different ways.


###Plotting in Base R

Using a basic plot, in base R, we can check that our data is normally distributed (this is a pre-condition for running many statistical analyses).

```{r plot1, echo=FALSE, cache=TRUE}

hist(d$vocab, col = "blue") # note that we add the color to make it easier to see the bars

```


Pie charts are something people often want to make-- though, be careful when using them. They are only good for visualizing big differences among few levels of data. For example, for highlighting how this sample mostly tested native-born individuals...

```{r plot2, echo=FALSE, cache=TRUE}

# To make a pie chart, first tabulate data. Here, the levels of nativeBorn, including NA.
# Use summary() for this, not table(), because NAs are excluded from that function.
pie_p <- summary(d$nativeBorn)
## turn into proportions. that's what we'll plot.
pie_p <- pie_p / sum(pie_p) 
pie(pie_p)
```


## Plotting with ggplot

To get a better examination of our data, we can use some more sophisticated plotting code. We will now make plots with ggplot2().

Let's start by looking at how vocabulary changes as people age.

We will start by creating a boxplot using ggplot2() functions.

```{r prep1, include=F, cache=T}
## Some prep for this:
## turn the continuous age variable into a 'factor' -- an ordered list
d$ageF <- as.factor(d$age)

## for this, we will use a subset of the data-- people 25 and under
## this represents people in college + recently graduated
ds <- d[d$age < 26, ]


#get rid of any rows that are all NAs
ds <- na.omit(ds)
## always good to look and check:
summary(ds)
```

Basic ggplot syntax:

Start with the command ggplot(), specifying the data to be plotted, and the variables you want to pass to the plot inside the function aes(). These are 'aesthetics'-- things that change in the plot, like x values, and y values.  (Also: colors, groups of data, shapes, transparency...)

Then, you tell the plot what type of graph to use with a second command-- a 'geom'. Here: geom_boxplot.

```{r plot3, echo=FALSE, cache=TRUE} 
# vocab by year: box plot
   ggplot(data=ds,aes(x = ageF, y = vocab))+  ## Putting the data and constant aes in the first call improves readability!
    geom_boxplot()
```

Here's another way to examine the same data, with violins rather than boxplot. Note that all we changed was the second line in the plot!

```{r plot4, echo=FALSE, cache=TRUE} 
# vocab by year: violin plot
   ggplot(data=ds,aes(x = ageF, y = vocab))+ 
    geom_violin()
```

That worked nicely for these data because they are unimodal (= there's only one main bulge in the center of each distribution).
Let's go back to boxes. We can pretty them up with some added code:

```{r plot5, echo=FALSE, cache=TRUE} 
# vocab by age: box plot
  ggplot(data=ds,aes(x = ageF, y = vocab))+ 
    geom_boxplot(size=2, alpha=0.7)+  ## describe the line width of the boxplot using size=, and the transparency using alpha=.  
    scale_x_discrete("Participant Age")+
    scale_y_continuous("Vocabulary Score")+
    ggtitle("Vocabulary by age")+ ## adding labels for x axis, y axis, and main title.
    theme_classic()+  ## this is a nice theme that gets rid of gridlines in plot.
    theme(text = element_text(size = 15), axis.text.x = element_text(size=10), legend.text = element_text(size = 15)) ## these commands change the size and location of the plot's text elements
```

We can also run a code chunk to save parts of a plot, and add to it. I'm saving everything but the geom command to object p.

```{r plotprep, echo=FALSE, cache=TRUE} 
p<- ggplot(data=ds,aes(x = ageF, y = vocab))+ 
    scale_x_discrete("Participant Age")+
    scale_y_continuous("Vocabulary Score")+
    ggtitle("Vocabulary by age")+
    theme_classic()+ 
    theme(text = element_text(size = 15), axis.text.x = element_text(size=10), legend.text = element_text(size = 15)) 
```
 
This will now give the same output as we got from plot6!
 
```{r plot6, echo=FALSE, cache=TRUE} 
p + geom_boxplot(size=2, alpha=0.7)
```

Try with some other geoms:

```{r plot7, echo=FALSE, cache=TRUE} 
p +
  geom_violin(draw_quantiles=c(.25,.5,.75)) + ## add a violin, with quantiles of the data added to it
  stat_summary(fun.y=mean, geom="point", size=2, color="red") ## also display the means as belly-buttons, using a summary function

## I added all of these things inside the geom and summary commands.
## This means that all conditions will get the same type of function applied to them.
## All conditions will have quantiles, and points that are always red.
```

What about looking at the actual individual data points?

```{r plot8, echo=FALSE, cache=TRUE} 
p + geom_point()
```

Those points were stacked on top of each other, which is why it looks like there are only a few data points by condition...
we can instead 'jitter' them so we can get a sense of where there's more data. We can also make the points slightly transparent using alpha. This will be much better!! 

```{r plot9, echo=FALSE, cache=TRUE} 
p + geom_jitter(alpha=.1)
```

For data where there are lots of points, we might want to plot an aggregate measure. we can use a bar plot for this. 

```{r plot10, echo=FALSE, cache=TRUE} 

# bar plot
p + geom_bar(stat = "summary", fun.y = "mean", size=2, alpha=0.7)

```

As a rule of thumb, bar plots should *always* show the variability inherent to the data. Otherwise, you have no idea whether differences between bars are reliable.

```{r plot11, echo=FALSE, cache=TRUE} 
## calculate standard error of the mean per point
## this is the sd/square root observations
## I like to assign to a value mVariable, as mnemmonic that this is the mean, not the raw scores

d_sum <- ddply(ds, .(ageF),summarise,sqrtN=sqrt(n()),sdVocab=sd(vocab),mVocab=mean(vocab)) 

# create variables with the upper and lower values
d_sum$Upper <- d_sum$mVocab + d_sum$sdVocab/d_sum$sqrtN
d_sum$Lower <- d_sum$mVocab - d_sum$sdVocab/d_sum$sqrtN
  
# add to bar plot
p + geom_bar(stat = "summary", fun.y = "mean", size=2, alpha=0.7)+
  geom_errorbar(data=d_sum,aes(x=ageF,y=mVocab,ymax=Upper, ymin=Lower),width=.5) ## for geoms, you can add new data and new aes()! just make sure to define what all the variables are, if the 'global' name set in the ggplot() call doesn't match the new data.
```

You might also want to 'zoom in' on the differences in the bar plot, to better see them. Mean scores vary between 4 and 6, but it is hard to see because the bar plot starts at 0. Instead, we can zoom in so that the y-axis plots only from 4 to 6.

```{r plot11a, echo=FALSE, cache=TRUE} 
# zoom in only on y values between 4 and 6
p + geom_bar(stat = "summary", fun.y = "mean", size=2, alpha=0.7)+
  geom_errorbar(data=d_sum,aes(x=ageF,y=mVocab,ymax=Upper, ymin=Lower),width=.5) +
  coord_cartesian(ylim = c(4, 6)) # a caption should be written with this plot explaining that the y-axis does not start at zero
```


Or we could make a similar a line plot. This is a little better for describing continuous patterns-- like change over time. Line plots should also, as a rule of thumb, provide a sense of variability. You can do with error bars, error ribbons, with smooths, or by just plotting the points in the data.

```{r plot12, echo=FALSE, cache=TRUE} 

# add to the summary data frame we made earlier: go back to numeric verison of age.  We can do this with code!
 d_sum$age <- as.numeric(as.character(d_sum$ageF))  ## as.numeric(as.character() is because R treats factors in an unexpected way.  try running as.numeric(d_sum$year) to see what it does....

## put the summarised data in ggplot() call!
  ggplot(data=d_sum,aes(x = age, y = mVocab))+
    geom_line( size=2, alpha=0.7)+
    geom_errorbar(aes(ymax=Upper, ymin=Lower))+  ## we can add error bars in a simpler way here, since the summarised data was specified earlier.
    scale_x_continuous("Participant Age")+
    scale_y_continuous("Vocabulary Score")+
    ggtitle("Vocabulary by age")+
    theme_classic()+
    theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))
```

Or use a ribbon instead of the error bars:


```{r plot12a, echo=FALSE, cache=TRUE} 

## 
  ggplot(data=d_sum,aes(x = age, y = mVocab))+
    geom_line( size=2, alpha=0.7)+
    geom_ribbon(aes(ymax=Upper, ymin=Lower), alpha=0.3)+  ## alpha specifies the transparency of the ribbon
    scale_x_continuous("Participant Age")+
    scale_y_continuous("Vocabulary Score")+
    ggtitle("Vocabulary by age")+
    theme_classic()+
    theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))
```




```{r plot13, echo=FALSE, cache=TRUE}
## we can also add the raw data points instead of error bars/ribbons: just plot the summarized line on top on the full data!
#This really serves to emphasize the spread of the data. 
  ggplot(data=d_sum,aes(x = age, y = mVocab))+
    geom_line( size=2, alpha=0.7)+
    geom_jitter(data=ds,aes(y=vocab),alpha=.04)+ # here we tell ggplot to use another data file
    scale_x_continuous("Participant Age")+
    scale_y_continuous("Vocabulary Score")+
    ggtitle("Vocabulary by age")+
    theme_classic()+
    theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))
# see that the lines look so different in the above two plots? That is because the y-axis scale changed!
```


Now, let's look at the trend for the full age range (going back to the original, yet cleaned, dateset d).
We can also save the full plot in workspace to call up later.

```{r plot14, echo=FALSE, cache=TRUE} 

plot1<- ggplot(data=d,aes(x = age, y = vocab))+
    geom_smooth(color="blue", lwd=2)+  # change the color and line width
    geom_jitter(data=d,aes(y=vocab),alpha=.03)+
    scale_x_continuous("Participant Age")+
    scale_y_continuous("Vocabulary Score")+
    ggtitle("Vocabulary by age")+
    theme_classic()+
    theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))

# and call it to display it
plot1

# And you can save it to a file
ggsave("plot1.png")
```

We can even examine the relationship between age and vocabulary scores over the years to make sure it's consistent. 

To make these plots, we will facet by year.

We'll skip the error bars/ smooths this time because the panels also provide some sense of variability, and the plot will get too complex fast with more stuff in it.

```{r plot15, echo=FALSE, warning=FALSE, cache=TRUE} 

# summarize vocabulary by age and year 
 d_sum_by_year<- ddply(d, .(year, age), summarise, mVocab = mean(vocab,na.rm=TRUE)) 
 d_sum_by_year$year <- as.numeric(as.character(d_sum_by_year$year)) # change year to be numeric

  # faceting by year
  # (you may need to expand the window to see better)
  ggplot(data=d_sum_by_year,aes(x = age, y = mVocab))+
    geom_line(size=1, alpha=0.8)+ # we made the lines thinner here (with size=) because the plots are smaller
    facet_wrap(year ~. ,scales = "free")+  ## facets make panels by one or more additional variables!
    scale_x_continuous("Participant Age")+
    scale_y_continuous("Vocabulary Score")+
    ggtitle("Vocabulary by year and age")+
    theme_classic()+
    theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))
```


But this is too hard to evaluate properly. It would be better to stack the lines on top of each other and color-code them by year, so we can actually see if there are any meaningful differences. We do this by adding "color=year" to the aes(). 

Here, we also add the "group" variable to tell ggplot to give one line per year. You can check to see what happens if you remove this grouping!


```{r plot16, echo=FALSE, warning=FALSE, cache=TRUE} 
  
ggplot(data=d_sum_by_year,aes(x = age, y = mVocab, color=as.factor(year), group=year))+
  geom_line(size=1, alpha=0.6)+
  scale_x_continuous("Age")+
  scale_y_continuous("Vocabulary Score")+
  ggtitle("Vocabulary by age and year")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))

```

Here, we treated "year" as a categorical value instead of a continuous variable. This means that each year gets a different color. In our case, it's a bit too much (we have 20 different years) and actually quite confusing (because the years are continuous), but this could be useful in other occasions. 
Instead, we can treat it as numeric, which will give each year a different hue of blue:

```{r plot17, echo=FALSE, warning=FALSE, cache=TRUE} 

# plot the relation between age and vocab by year
ggplot(data=d_sum_by_year,aes(x = age, y = mVocab, color=as.numeric(year), group=year))+
  geom_line(size=1, alpha=0.6)+
  scale_x_continuous("Participant Age")+
  scale_y_continuous("Vocabulary Score")+
  ggtitle("Vocabulary by age and year")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))

```

We can also highligh a specific year of interest using gg_highlight:

```{r plot18, echo=FALSE, warning=FALSE, cache=TRUE} 

ggplot(data=d_sum_by_year,aes(x = age, y = mVocab, color=as.numeric(year), group=year))+
  geom_line(size=1, alpha=0.6)+
  gghighlight(year==2008)+ # highlight 2008
  scale_x_continuous("Participant Age")+
  scale_y_continuous("Vocabulary Score")+
  ggtitle("Vocabulary by age and year")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))
```

Or a range of relevant years:

```{r plot18b, echo=FALSE, warning=FALSE, cache=TRUE} 

ggplot(data=d_sum_by_year,aes(x = age, y = mVocab, color=as.numeric(year), group=year))+
  geom_line(size=1, alpha=0.6)+
  gghighlight(year>2000 & year < 2011)+ # highlight data from between 2000-2011
  scale_x_continuous("Participant Age")+
  scale_y_continuous("Vocabulary Score")+
  ggtitle("Vocabulary by age and year")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))


```


Now, let's continue to examine the relation between age and vocabulary scores in our data set by adding another feature of interest - Nativeness.
How much does nativeness matter? Let's check this by adding a different color to the plot based on nativeness. 

```{r plot19, echo=FALSE, cache=TRUE}

# plotting the vocabulary scores by age and nativeness using a simple scatter plot with jittered points
ggplot(data=d,aes(x = age, y = vocab, color=nativeBorn))+ 
  geom_jitter(size=2, alpha=0.7)+   ##points, but jittered 
  scale_x_continuous("Age")+
  scale_y_continuous("Vocabulary Score")+
  ggtitle("Vocabulary by age and nativeness")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))

```

OK, this is obviously not very useful. There are just too many points!
 
Try summarizing the points and looking at the averages. 


```{r plot20, echo=FALSE, cache=TRUE}
#to prep, make a new data frame where we summarize the average vocabulary scores by age and nativeness
d_sum_by_age<- ddply(d, .(age, nativeBorn), summarise, mVocab = mean(vocab,na.rm=TRUE)) 
d_sum_by_age <- na.omit(d_sum_by_age) # remove n/a

# plot vocab by age and nativeness
ggplot(data=d_sum_by_age,aes(x = age, y = mVocab, color=nativeBorn))+ 
  geom_point( size=2, alpha=0.7)+
  geom_smooth(method = 'loess')+ # because we asked for different colors in the aes() above, we will also get different colored lines!
  scale_x_continuous("Age")+
  scale_y_continuous("Vocabulary Score")+
  ggtitle("Vocabulary by age and nativeness")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))
```

We also want to look at gender, so we can add that too.

First, we'll summarize the data by gender, age and nativeness. Then, we can make a nice clear plot with faceting.
Try facet_grid instead of facet_wrap this time.
And also, I want to change the colors:
 
```{r plot21, echo=FALSE, cache=TRUE} 

d_sum_by_age_gender<- ddply(d, .(age, gender, nativeBorn), summarise, mVocab = mean(vocab,na.rm=TRUE)) 
d_sum_by_age_gender <- na.omit(d_sum_by_age_gender) # remove n/a

plot2 <- # save a plot
ggplot(data=d_sum_by_age_gender,aes(x = age, y = mVocab, color=nativeBorn))+
  geom_point(size=2, alpha=0.7)+
  facet_grid(.~gender)+
  scale_x_continuous("Participant Age")+
  scale_y_continuous("Vocabulary Score")+
  ggtitle("Vocabulary by age, nativeness, and gender")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))+
  scale_color_manual(values=c("chocolate","purple")) 

# you can find the full list of colour names here: http://sape.inf.usi.ch/quick-reference/ggplot2/colour
# you can also add in RGB/hex values for colours, just search your favourite colour!

 plot2 # show the plot

```
 
What do you see? Does nativeness have a similar effect on both genders?



### Time to do some plotting yourself! :)

1. Creat a new r code chunk and give it a descriptive name.

2. Make a new plot of the data d. You could try:

  - Summarising the full data across some other variable (using the function ddply() )
  
  - Faceting the data in different ways (What happens if you replace the . in facet_grid with a variable?)
  
  - Combining multiple geoms!  (What happens if you add geom_smooth on top of plot 21?)
  
  - Changing the colors to make certain contrasts pop out (what if you swap the order of the colors in plot 21?)
  
  - Changing the transparency, size of points, or size of text.
  
  - Changing the shape of points-- what do you think the function for changing the shape of points should be? (See the legend below for help.)
 
 
![](http://www.sthda.com/sthda/RDoc/images/points-symbols.png)

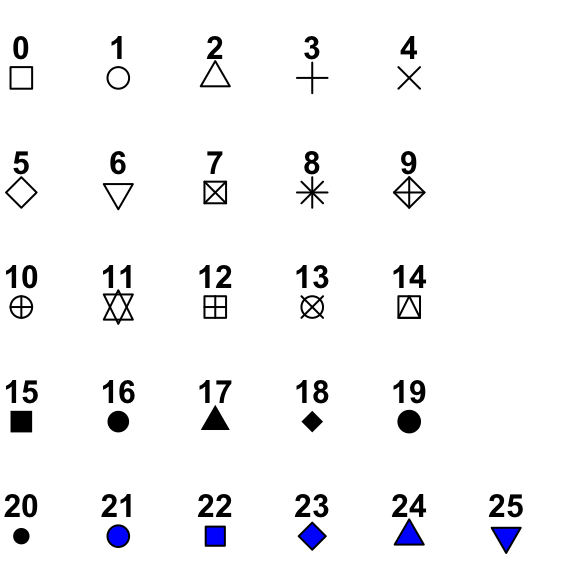
### Combining Plots

You can also combine different plots to one grid using the "cowplot" package. For that, you'll need the plots you named and saved into your workspace:

```{r plot22, echo=FALSE, warning=FALSE, cache=TRUE}
# create a figure with different plots, labeled A,B, one below the other
full_fig <- plot_grid(plot2, plot1, labels = "AUTO", ncol=1, nrow=2, align = 'v')

full_fig # show the combined figure (you will probably need to expand the window to see)

save_plot("fig.jpg", full_fig, base_height=3, base_width=6, ncol=1, nrow=2) # save the plot in the folder

#when you open the file you created, you'll see it's not stretched anymore :)
```

### Animating Plots

If you have a line plot where the x-axis representes some change over time (e.g., with age,  with year, with testing blocks), you could try to animate it.
This is really cool and useful for presentations!

For this, we'll use the gg_animate package, and some packages to create GIFs.

```{r animated plot, echo=FALSE, warning=FALSE, cache=TRUE}

# let's say this is our basic plot - showing the change in vocabulary size as a function of age for both natives and non-natives
plot3 <- ggplot(data=d_sum_by_age,aes(x = age, y = mVocab, color=nativeBorn))+ 
  geom_line(lwd=2)+
  scale_x_continuous("Age")+
  scale_y_continuous("Vocabulary Score")+
  ggtitle("Vocabulary by age and nativeness")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15)) 


# Here comes the animation code!
# Note: this may take a few seconds! 

ani_plot <- plot3 +
  transition_reveal(age)+
  ease_aes('linear')

# show the animated plot (on the right side bar)
# this might take a minutes to run...
ani_plot

# And save your animation as a GIF
anim_save(filename="animated_plot.gif", animation = ani_plot)

```



## Analysis time!

Let's dig deeper into the relationship between education, age, and native language background. We will model this with a mixed-effects regression.

First, let's prepare our variables by centering the continuous ones and setting up the contrasts-- specifying how the regression model deals with categorical predictors. This causes the model to make the comparisons we want it to make. 

```{r prepare for regression, include=FALSE, cache=TRUE}

# Before we start the analyses, center our continuous variables. 
# Since zero has a special status in regression models, it is useful to put zero in the middle of the range.
d$c.age <- d$age - mean(d$age, na.rm=T)
d$c.educ <- d$educ - mean(d$educ,na.rm=T)

# and then set our contrasts. this tells the model how to think about categorical variables, since they have to be treated as numbers for regression (but aren't numbers!)

# Gender:
levels(d$gender) # check the levels of this variable
contrasts(d$gender) <- c(0,1) # set female as baseline
contrasts(d$gender) # make sure this is what we did :)

#NativeBorn
# Now let's do the same for nativeBorn
levels(d$nativeBorn) # check the levels of this variable
contrasts(d$nativeBorn) <- c(1,0) # set natives as baseline
contrasts(d$nativeBorn)
```

Now, let's make a model based on our predictions.

We will run an (overly) simple model in terms of the random effects (the 1|year part) because it can take a while to figure this out.
We'll also use the rule-of-thumb that t-value > 2 means a significant effect. 

```{r regression, echo=FALSE, cache=TRUE}

# regression model

reg1<- lmer(vocab ~                             #dependent measure
              c.age*c.educ*nativeBorn*gender+   ## look at the combination of age, education, nativeness, and gender as fixed effects, and their interactions
              (1|year),  ## year of measurement is our random effect: the equivalent of a repeated measure in ANOVA
          data=d, REML=T)

summary(reg1)
```

To make this appear as pretty table, we can use the "kable" function.

```{r regression table, echo=FALSE, cache=TRUE}

# make a dataframe with the model output

reg1_table <- data.frame(coef(summary(reg1))) # save the coefficients to a data frame

colnames(reg1_table) <- c("Estimate", "Std.Error", "t-value") # add the column names 
rownames(reg1_table) <- c("(Intercept)", "Age", "Years of Education", "Nativeness (Non-native vs. Native)", "Gender (Male vs. Female)", "Age X Education", "Age X Nativeness","Education X Nativeness","Age X Gender","Education X Gender","Nativeness X Gender", "Age X Education X Nativeness ","Age X Education X Gender","Age X Nativeness X Gender", "Education X Nativeness X Gender","Age X Education X Nativeness X Gender") # change the row names to be more informative (not just the variable name, but the full description)

kable(reg1_table, digits = 6, caption = "Vocabulary score by age, education, nativeness and gender") # print the pretty table

```


But what's actually going on? 

It's fairly easy to understand the main effects of education, age, gender and nativeness:

- Age is a significant positive predictor of vocab scores (higher age = higher score)
- Nativeness is a significant negative predictor of vocab scores (non native = lower score than native)
- Gender is a significant negative predictor of vocab scores (males = lower score than females)
- Education is a significant positive predictor of vocab scores (higher education = higher score)


But when it comes to the interactions (and especially, the triple interaction), it's harder to interpret.

The sign of the interactions tells us about our effects.

We can try to use the sign of the interactions to understand our effects.

For exmaple:
- the effect of age is positive (higher age = higher score)
- the effect of gender is negative (males = lower score)
- the interaction between age and gender is negative (--> the positive effect of age on vocab score is smaller for males)

But this is not trivial for everyone, and can be confusing.

Also, once we get to the triple interaction of age, education, and gender, this gets much harder to understand by just looking at the signs...

*So - we can plot the model using the "effects" package! :)*

## Plotting the model

First, let's confirm that we understood the main effects:

```{r regression plot1, warning=FALSE, echo=FALSE, cache=TRUE}

plot(effect("c.age", reg1))

```

```{r regression plot2,  warning=FALSE, echo=FALSE, cache=TRUE}

plot(effect("c.educ", reg1))

```

```{r regression plot3, warning=FALSE, echo=FALSE, cache=TRUE}

plot(effect("gender", reg1))

```

```{r regression plot4, warning=FALSE, echo=FALSE, cache=TRUE}

plot(effect("nativeBorn", reg1))

```

Now let's plot the interactions:

*Note: When plotting effects you need to give the name of the effect in the same order as you wrote it into the model e.g. c.age BY gender. If you write it in a different order, e.g. gender BY c.age, it will not recognize this term and the plot will break *

```{r regression plot5,  warning=FALSE, echo=FALSE, cache=TRUE}

plot(effect("c.age*gender", reg1))

```

Indeed, we can see that the relationship between age and vocabulary scores is weaker (=smaller slope) for males.

```{r regression plot6, warning=FALSE, echo=FALSE, cache=TRUE}

plot(effect("c.age*nativeBorn", reg1))

```

It might be useful to plot these slopes from the model on top on the raw data.
This is very easy to do in ggplot: we can combine data from different files together. 

```{r regression plot1 model + data, warning=FALSE, echo=FALSE, cache=TRUE}

# save the effect to a dataframe
model_plot <- effect("c.age*nativeBorn", reg1, xlevels=15)
model_plot <-as.data.frame(model_plot)
model_plot$c.age <- model_plot$c.age +46 # make centered age uncentered again 
model_plot$nativeBorn <- factor(model_plot$nativeBorn, levels=c("Non-native", "Native")) # make sure our variable is the same (you can check to see what happens if we don't do this...)


 plot4 <- ggplot()+  ## this plot pulls a lot of stuff together, so keep the specifications in the geoms
  geom_point(data=d_sum_by_age,aes(x = age, y = mVocab, color=nativeBorn),lwd=2, alpha=0.4)+
  geom_ribbon(data = model_plot, aes(x=c.age, ymin = lower, ymax = upper, fill = nativeBorn), alpha = 0.15)+ 
  geom_line(data=model_plot,aes(c.age, fit, color=nativeBorn),lwd=3)+
   scale_x_continuous("Age")+
  scale_y_continuous("Mean vocabulary score")+
  ggtitle("Mean vocabulary score by age and nativeness")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))

 plot4

```

Great! We see that except for the fact that natives have higher scores, nativeness is changing the relationship between age and vocabulary scores (i.e., the slope is steeper for non-natives).

### Plotting (and understanding) triple interactions

```{r regression plot7, echo=FALSE, cache=TRUE}

plot(effect("c.age*nativeBorn*gender", reg1))
```

This plot is actually not so clear and it's hard to see the differences, but the idea is that the significant relationship between age and gender (i.e., males showing a weaker relationship) is somewhat modulated by nativeness (so it is true only for the natives).

Maybe we can try to plot the model AND the raw data together to get a better picture.

```{r regression plot2 model+data, echo=FALSE, cache=TRUE}

# save the model coefficients

model_plot2 <- effect("c.age*nativeBorn*gender", reg1, xlevels=10)
model_plot2 <-as.data.frame(model_plot2)
model_plot2$c.age <- model_plot2$c.age +46 # make centered age uncentered again 

ggplot()+
  geom_point(data=d_sum_by_age_gender,aes(x = age, y = mVocab, color=gender),lwd=1, alpha=0.4)+
  facet_grid(.~nativeBorn,scales = "free")+
  geom_ribbon(data = model_plot2, aes(x=c.age, ymin = lower, ymax = upper, fill = gender), alpha = 0.15)+
  geom_line(data=model_plot2,aes(c.age, fit, color=gender),lwd=3)+
   scale_x_continuous("Age")+
  scale_y_continuous("Mean vocabulary score")+
  ggtitle("Mean vocabulary score by age, gender and nativeness")+
  theme_classic()+
  theme(text = element_text(size = 15), axis.text.x = element_text(size=15), legend.text = element_text(size = 15))

```


### Time to do some model plotting yourself! :)


1. Creat a new r code chunk, and give it a useful name 

2. Plot the interaction between nativeness and gender

3. Plot the interaction between nativeness and education

4. Plot the interaction between gender and education

5. Plot the triple interaction between gender, education and nativeness

6. Plot the raw data + model estimates for one of the interactions above 

7. Check: do the plots fit the model's output and the significance of the interactions?




## Side note about contrasts for categorical variables:

The "basic" coding schemes are:
- *Dummy coding* = compares levels to a baseline level (this is done with 0's and 1's)
- *Sum/deviation coding* = compares levels to the grand mean (this is done with -1's and 1's)

There are *many* other coding schemes to make many more comparisons (even user-defined ones). You can check out this webpage for useful examples and coding matrices: <https://stats.idre.ucla.edu/r/library/r-library-contrast-coding-systems-for-categorical-variables/>

Using different coding schemes asks different questions, and makes different comparisons. It will therefore yield different coefficients (estimates). 
_But the overall model fit stays the same, and **the significance of the predictor remains the same**!!_

If you want to be sure, let's rerun the same model after changing the contrasts of "nativeBorn" to c(-1,1) and check for yourself!

```{r contrasts, echo=FALSE, cache=TRUE}

# change the contrasts for nativeness so it's compared to the grand mean instead

contrasts(d$nativeBorn) <- c(1,-1) # non-natives compared to the grand mean (instead of the reference level)

# regression model

reg2<- lmer(vocab ~
            c.age*nativeBorn*gender + c.educ*nativeBorn*gender+ (1|year),
          data=d, REML=T)


#let's make a pretty table out of it
reg2_table <- data.frame(coef(summary(reg2))) # save the coefficients to a data frame
reg2_table$p <- 2 * (1 - pnorm(abs(reg2_table$t.value)))
colnames(reg2_table) <- c("Estimate", "Std.Error", "t-value","p-value") # add the column names 
rownames(reg2_table) <- c("(Intercept)", "Age", "Nativeness (Non-native vs. Native)", "Gender (Male vs. Female)", "Years of Education", "Age X Nativeness","Age X Gender","Nativeness X Gender","Nativeness X Education","Education X Gender", "Age X Nativeness X Gender", "Education X Nativeness X Gender") # change the row names to be more informative (not just the variable name, but the full description)

# compare the tables 
kable(reg1_table, digits = 6, caption = "Original model") # print the pretty table

kable(reg2_table, digits = 6, caption = "Model with sum-coding") # print the pretty table

```