|
| 1 | +# NSFNet4 |
| 2 | + |
| 3 | +<a href="https://aistudio.baidu.com/projectdetail/7305374" class="md-button md-button--primary" style>AI Studio快速体验</a> |
| 4 | + |
| 5 | +=== "模型评估命令" |
| 6 | + |
| 7 | + ``` sh |
| 8 | + # VP_NSFNet4 |
| 9 | + # linux |
| 10 | + wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/NSFNet/NSF4_data.zip -P ./data/ |
| 11 | + unzip ./data/NSF4_data.zip |
| 12 | + # windows |
| 13 | + # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/NSFNet/NSF4_data.zip --output ./data/NSF4_data.zip |
| 14 | + # unzip ./data/NSF4_data.zip |
| 15 | + python VP_NSFNet4.py mode=eval data_dir=./data/ EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/nsfnet/nsfnet4.pdparams |
| 16 | + ``` |
| 17 | + |
| 18 | +=== "模型训练命令" |
| 19 | + |
| 20 | + ``` sh |
| 21 | + # VP_NSFNet4 |
| 22 | + # linux |
| 23 | + wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/NSFNet/NSF4_data.zip -P ./data/ |
| 24 | + unzip ./data/NSF4_data.zip |
| 25 | + # windows |
| 26 | + # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/NSFNet/NSF4_data.zip --output ./data/NSF4_data.zip |
| 27 | + # unzip ./data/NSF4_data.zip |
| 28 | + python VP_NSFNet4.py data_dir=./data/ |
| 29 | + |
| 30 | + ``` |
| 31 | + |
| 32 | +## 1. 背景简介 |
| 33 | + |
| 34 | + 最近几年, 深度学习在很多领域取得了非凡的成就, 尤其是计算机视觉和自然语言处理方面, 而受启发于深度学习的快速发展, 基于深度学习强大的函数逼近能力, 神经网络在科学计算领域也取得了成功, 现阶段的研究主要分为两大类, 一类是将物理信息以及物理限制加入损失函数来对神经网络进行训练, 其代表有 PINN 以及 Deep Ritz Net, 另一类是通过数据驱动的深度神经网络算子, 其代表有 FNO 以及 DeepONet。这些方法都在科学实践中获得了广泛应用, 比如天气预测, 量子化学, 生物工程, 以及计算流体等领域。而为充分探索PINN对流体方程的求解能力, 本次复现[论文](https://arxiv.org/abs/2003.06496)作者设计了NSFNets, 并且先后使用具有解析解或数值解的二维、三维纳韦斯托克方程以及使用DNS方法进行高精度求解的数据集作为参考, 进行正问题求解训练。论文实验表明PINN对不可压纳韦斯托克方程具有优秀的数值求解能力, 本项目主要目标是使用PaddleScience复现论文所实现的高精度求解纳韦斯托克方程的代码。 |
| 35 | + |
| 36 | +## 2. 问题定义 |
| 37 | + |
| 38 | +本问题所使用的为最经典的PINN模型, 对此不再赘述。 |
| 39 | + |
| 40 | +主要介绍所求解的几类纳韦斯托克方程: |
| 41 | + |
| 42 | +不可压纳韦斯托克方程可以表示为: |
| 43 | + |
| 44 | +$$\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u} \cdot \nabla) \mathbf{u} =-\nabla p+\frac{1}{Re} \nabla^2 \mathbf{u} \quad \text { in } \Omega, $$ |
| 45 | + |
| 46 | +$$\nabla \cdot \mathbf{u} =0 \quad \text { in } \Omega, $$ |
| 47 | + |
| 48 | +$$\mathbf{u} =\mathbf{u}_{\Gamma} \quad \text { on } \Gamma_D, $$ |
| 49 | + |
| 50 | +$$\frac{\partial \mathbf{u}}{\partial n} =0 \quad \text { on } \Gamma_N.$$ |
| 51 | + |
| 52 | +### 2.1 JHTDB 数据集 |
| 53 | + |
| 54 | +数据集为使用DNS求解Re=999.35的三维不可压强迫各向同性湍流的高精度数据集, 详细参数可见[readme](https://turbulence.pha.jhu.edu/Forced_isotropic_turbulence.aspx). |
| 55 | + |
| 56 | +## 3. 问题求解 |
| 57 | + |
| 58 | +### 3.1 模型构建 |
| 59 | + |
| 60 | +本文使用PINN经典的MLP模型进行训练。 |
| 61 | + |
| 62 | +``` py linenums="137" |
| 63 | +--8<-- |
| 64 | +examples/nsfnet/VP_NSFNet4.py:137:137 |
| 65 | +--8<-- |
| 66 | +``` |
| 67 | + |
| 68 | +### 3.2 数据生成 |
| 69 | + |
| 70 | +先后取边界点、初值点、以及用于计算残差的内部点(具体取法见[论文](https://arxiv.org/abs/2003.06496)节3.3)以及生成测试点。 |
| 71 | + |
| 72 | +``` py linenums="139" |
| 73 | +--8<-- |
| 74 | +examples/nsfnet/VP_NSFNet4.py:139:167 |
| 75 | +--8<-- |
| 76 | +``` |
| 77 | + |
| 78 | +### 3.3 归一化处理 |
| 79 | + |
| 80 | +为将所取较小长方体区域改为正方体区域, 我们将归一化函数嵌入网络训练前。 |
| 81 | + |
| 82 | +``` py linenums="169" |
| 83 | +--8<-- |
| 84 | +examples/nsfnet/VP_NSFNet4.py:169:174 |
| 85 | +--8<-- |
| 86 | +``` |
| 87 | + |
| 88 | +### 3.4 约束构建 |
| 89 | + |
| 90 | +由于我们边界点和初值点具有解析解, 因此我们使用监督约束, 其中alpha和beta为该损失函数的权重, 在本代码中与论文中描述一致, 都取为100。 |
| 91 | + |
| 92 | +``` py linenums="226" |
| 93 | +--8<-- |
| 94 | +examples/nsfnet/VP_NSFNet4.py:226:237 |
| 95 | +--8<-- |
| 96 | +``` |
| 97 | + |
| 98 | +使用内部点构造纳韦斯托克方程的残差约束 |
| 99 | + |
| 100 | +``` py linenums="239" |
| 101 | +--8<-- |
| 102 | +examples/nsfnet/VP_NSFNet4.py:239:262 |
| 103 | +--8<-- |
| 104 | +``` |
| 105 | + |
| 106 | +### 3.5 评估器构建 |
| 107 | + |
| 108 | +使用在数据生成时生成的测试点构造的测试集用于模型评估: |
| 109 | + |
| 110 | +``` py linenums="271" |
| 111 | +--8<-- |
| 112 | +examples/nsfnet/VP_NSFNet4.py:271:276 |
| 113 | +--8<-- |
| 114 | +``` |
| 115 | + |
| 116 | +### 3.6 优化器构建 |
| 117 | + |
| 118 | +与论文中描述相同, 我们使用分段学习率构造Adam优化器, 其中可以通过调节epoch_list来调节训练轮数。 |
| 119 | + |
| 120 | +``` py linenums="281" |
| 121 | +--8<-- |
| 122 | +examples/nsfnet/VP_NSFNet4.py:281:283 |
| 123 | +--8<-- |
| 124 | +``` |
| 125 | + |
| 126 | +### 3.7 模型训练与评估 |
| 127 | + |
| 128 | +完成上述设置之后, 只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`。 |
| 129 | + |
| 130 | +``` py linenums="284" |
| 131 | +--8<-- |
| 132 | +examples/nsfnet/VP_NSFNet4.py:284:302 |
| 133 | +--8<-- |
| 134 | +``` |
| 135 | + |
| 136 | +最后启动训练即可: |
| 137 | + |
| 138 | +``` py linenums="303" |
| 139 | +--8<-- |
| 140 | +examples/nsfnet/VP_NSFNet4.py:303:304 |
| 141 | +--8<-- |
| 142 | +``` |
| 143 | + |
| 144 | +## 4. 完整代码 |
| 145 | + |
| 146 | +``` py linenums="1" title="NSFNet.py" |
| 147 | +--8<-- |
| 148 | +examples/nsfnet/VP_NSFNet4.py |
| 149 | +--8<-- |
| 150 | +``` |
| 151 | + |
| 152 | +## 5. 结果展示 |
| 153 | + |
| 154 | +### NSFNet4 |
| 155 | + |
| 156 | +如图所示, NSFNet的结果在时间上的误差相对平稳, 并未出现传统方法中经常出现的误差累积问题。其中, 虽然在训练过程中三个方向的速度并未被设置权重, 但是训练结果可以看出, 神经网络在第一个速度方向u上面逼近效果最好, 在第三个速度方向w上面逼近效果次之, 在第二个速度v上面逼近效果最差且出现较为明显的误差累积现象。 |
| 157 | + |
| 158 | + |
| 159 | +如图所示, 在x=12.47的y-z平面的轮廓图, 第一个为速度u的轮廓图, 第二个为速度v的轮廓图, 第三个为速度w的轮廓图, 第四个为速度p的轮廓图。可以看出, 速度u的轮廓图相对于v, w, p来说较为光滑。 |
| 160 | + |
| 161 | + |
| 162 | +如图所示, 在z=4.61的x-y平面的轮廓图, 第一个为速度u的轮廓图, 第二个为速度v的轮廓图, 第三个为速度w的轮廓图, 第四个为速度p的轮廓图。可以看出, 速度u的轮廓图相对于v, w, p来说较为光滑。 |
| 163 | +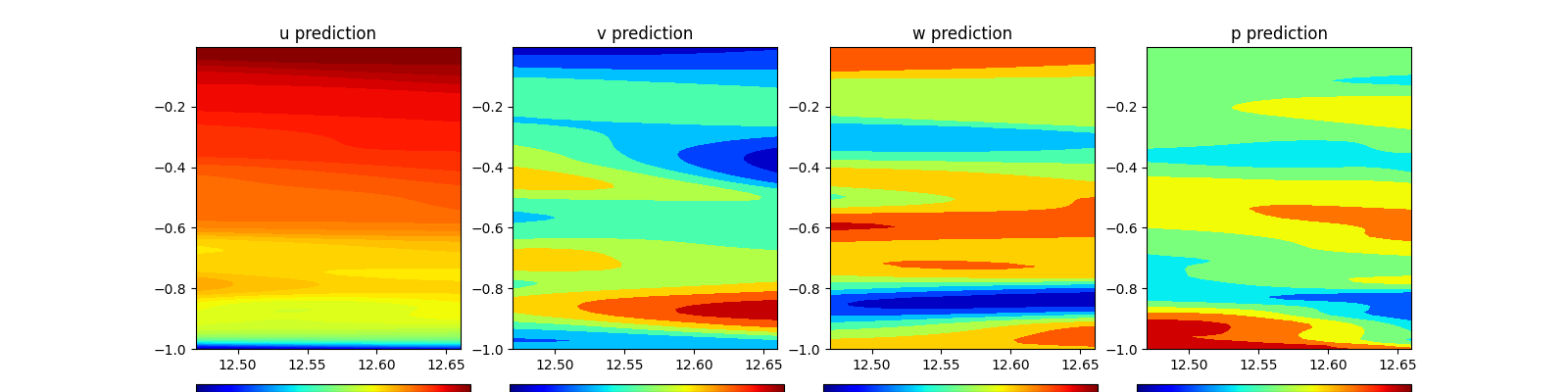 |
| 164 | + |
| 165 | +综上所述, 虽然u, v, w三个速度方向都是需要神经网络进行训练, 但是对于JHTDB数据集来说, u方向数据较为光滑, 更容易被神经网络所学习。因此在后续研究中, 可以尝试对三个不同方向的分量分而治之, 加大复杂分量方向的训练强度, 减少简单分量方向的训练强度。 |
| 166 | + |
| 167 | +## 6. 结果说明 |
| 168 | + |
| 169 | +我们使用PINN对不可压纳韦斯托克方程进行数值求解。在PINN中, 随机选取的时间和空间的坐标被当作输入值, 所对应的速度场以及压强场被当作输出值, 使用初值、边界条件当作监督约束以及纳韦斯托克方程本身的当作无监督约束条件加入损失函数进行训练。我们使用高精度JHTDB数据集进行训练。通过损失函数的下降可以证明神经网络在求解纳韦斯托克方程中的收敛性, 表明PINN拥有对不可压强迫各项同性湍流的求解能力。而通过实验结果表明, PINN可以很好的逼近对应的高精度不可压强迫各项同性湍流数据集, 并且, 我们发现增加边界约束以及初值约束的权重可以使得神经网络拥有更好的逼近效果。相比之下, 在误差允许范围内, 使用PINN求解该纳韦斯托克方程比原本使用DNS方法的推理速度更快。 |
| 170 | + |
| 171 | +## 7. 参考资料 |
| 172 | + |
| 173 | +- [NSFnets (Navier-Stokes Flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations](https://arxiv.org/abs/2003.06496) |
| 174 | + |
| 175 | +- [Github NSFnets](https://github.com/Alexzihaohu/NSFnets/tree/master) |
0 commit comments