Doubt with residual parameters calculation

[fedebenelli]

I have a doubt on how you calculate the residual Helmholtz energy, specifically the first derivative with the reduced density.

According to the GERG-2008 paper the polinomial term should be:

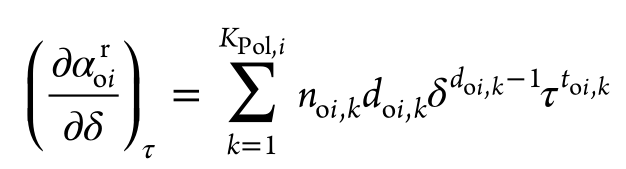
In your code, around line 555:

for(let k = 1; k <= kpol[i]; k++){
          ndt = x[i] * delp[doik[i][k]] * taup[i][k];
          ndtd = ndt * doik[i][k];
          ar[0][1] = ar[0][1] + ndtd;

For what I understood, taup[i][k] equals to n_{oi,k} * tau ^ t_{oi,k}. So each term of the derivative is calculated like:

delta^d_{oi,j} * n_{oi,k} * tau ^ t_{oi,k} * d_{oi,j}
When the term of the paper is:
delta^(d_{oi,j}-1) * n_{oi,k} * tau ^ t_{oi,k} * d_{oi,j}

I'm sure your code work, since I've tested a bit of it and reached good results, could you tell me what I'm reading wrongly?
(I'm trying to make my own implementation on Python and Fortran and not getting the expected results)

Thank you for your time!

[TorrensJoaquin]

It's possible that you have the same mistake i had. Let me know if i'm right.
Let me use uppercase letters for DELTA = d/dr and lowercase for the partial derivative operator = delta.
When you first look at the meaning of the output in the comments. It seems like a[0][1] is delta aij/ delta DELTA. But if you look at it again you will notice that is DELTA * delta aij/ delta DELTA. That cancel out the -1 in the exponent.

//Outputs;
// ar(0,0) - Residual Helmholtz energy (dimensionless, =a/RT)
// ar(0,1) -     delta*partial  (ar)/partial(delta)
// ar(0,2) -   delta^2*partial^2(ar)/partial(delta)^2
// ar(0,3) -   delta^3*partial^3(ar)/partial(delta)^3
// ar(1,0) -       tau*partial  (ar)/partial(tau)
// ar(1,1) - tau*delta*partial^2(ar)/partial(tau)/partial(delta)
// ar(2,0) -     tau^2*partial^2(ar)/partial(tau)^2

PS:
I'm aware of two implementation in FORTRAN
https://github.com/n-centrix/ISO20765-Part2
https://github.com/usnistgov/AGA8/tree/master/AGA8CODE/FORTRAN (From NIST - Ian Bell and Eric Lemmon)
I'm not aware of any implementation on python. Looking forward to see it.

[fedebenelli]

Thanks for the quick response!
Ohh, now I understand, thanks for the clarification! Is there any reason you do it this way besides avoiding using the "-1"?

[TorrensJoaquin]

When you run CalculateDensity. This routine is inside the loop of the Newton Raphson method.
I understand that Eric tried to avoid expensive computations inside the loop.

• Sadly, the original version was on VBA. Where you can't upload to memory for more than one determination. (You could use a matrix formula but is not very comfortable). So this effort got diluted.

• I've tried to replace this with a binary search (more robust but less effective). But low improvements were found.