eqtl计算方法.md

eQTL计算原理

全基因组关联分析（GWAS）

定义：对于多个个体在全基因组范围的遗传变异多态性（SNP）进行检测，获得基因型，将基因型与表型进行统计学分析，根据显著性等关系筛选出最有可能影响该性状的遗传变异，目的是通过这种方法找出与变异相关的基因。

Expression Quantitative Trait Loci(eQTL) analysis

表达数量位置的基因座，它指的是染色体上一些能特定调控mRNA和蛋白表达水平的区域，其mRNA/蛋白质的表达水平量与数量性状成比例关系。eQTL analysis是将基因表达水平的变化和基因型连接起来，研究遗传突变与基因表达的相关性。

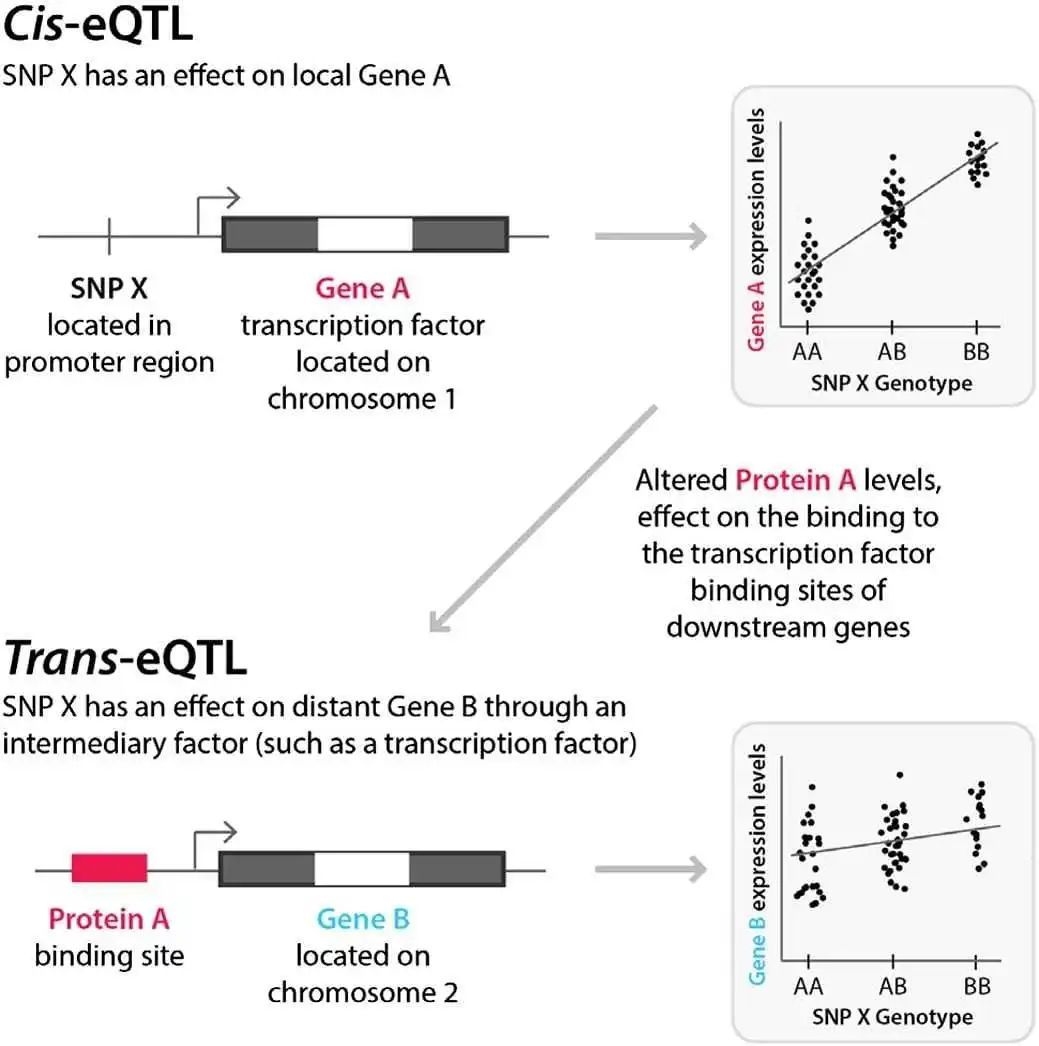
eQTL可以分为顺式和反式两种

eQTL分析的本质是以全部的DNA变异位点为自变量，轮流以每种mRNA表达量为因变量，用大量的个体数据做样本进行线性回归，得到每一个SNP位点和每一个mRNA表达量间的关系。

线性回归（linear regression）

回归指的是在数据建模中因变量是定量变量。

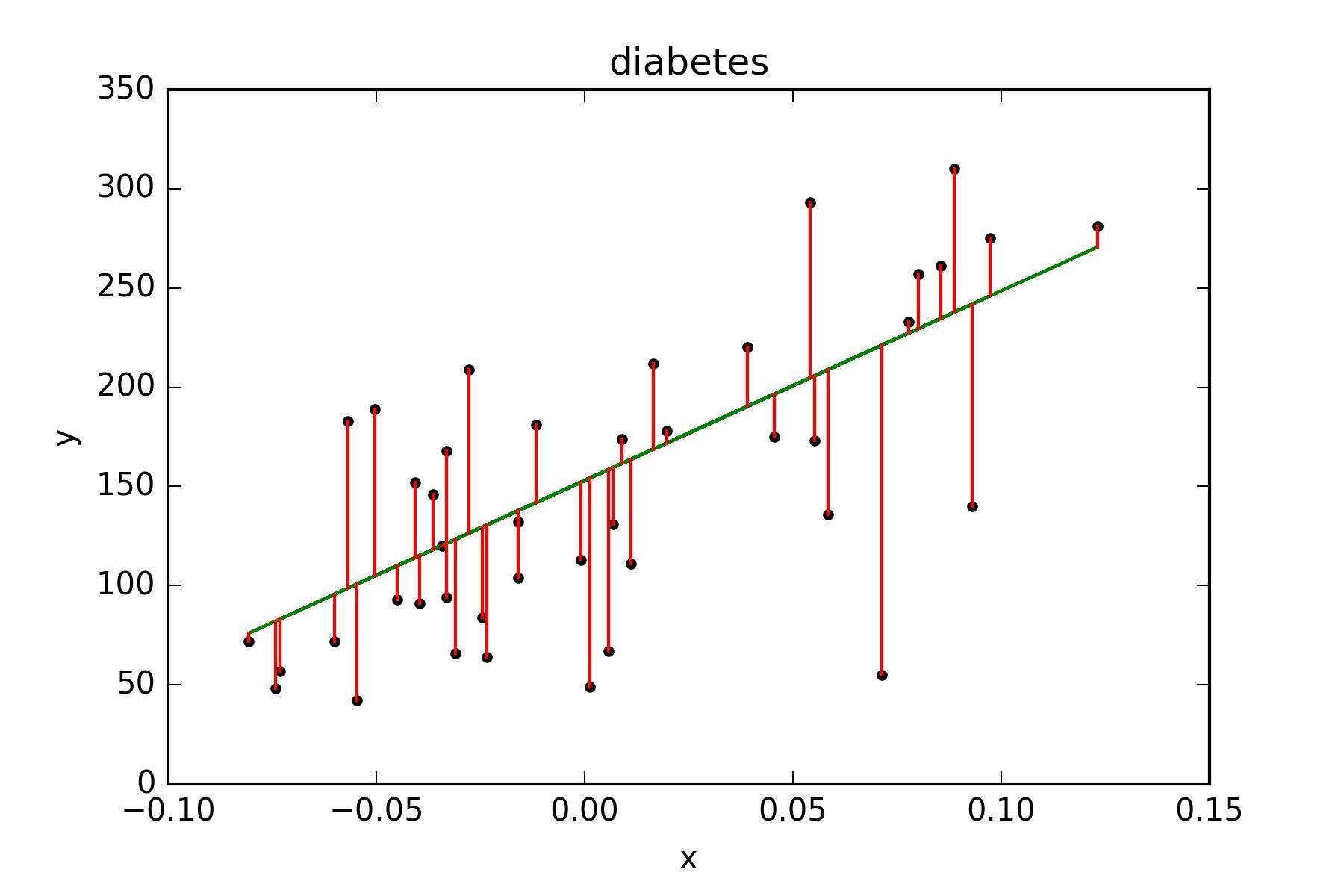
线性回归是指，对于自变量 $x$和因变量$y$可以写成下列的线性模型： $$ Y= \mu + \beta X +\epsilon $$ 其中$\mu$是截距，$\beta$是斜率，$\epsilon$是随机误差。

我们要求的是，对于给定的数据点($x_1,y_1$),($x_2,y_2$),...,($x_n,y_n$)，存在一个合适的直线$$\hat{y}= \hat{\mu} +\hat{\beta}x$$能更好的拟合我们的数据，最长使用的是最小二乘回归：每个样本点到这条直线的数值距离的平方和最小。最小二乘回归也就是求残差平方和（SSE）的最小值。

其他的回归方式：多元线性回归，方差分析等。

实际应用

在做eQTL分析时，对于回归模型$Y= \mu + \beta X +\epsilon$其中：

$Y$指的是基因的表达水平；

$X$指的是考虑的SNP的基因类型，编码为0,1,2；

$\mu$指的是AA基因型的表达水平;

$\beta$指的是每一个等位基因B对Y的表达有多大的影响;

$\epsilon$指的就是随机误差。

Matrix eQTL

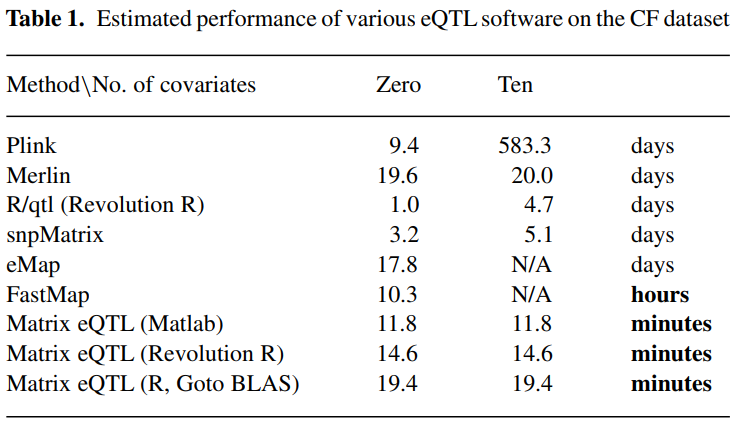
以该方法为例，这是一个研究团队在12年提出的一个R包，相较于其他的的计算方法，它在运行时间上是更有优势的。

这个R包需要genotype,expression,gene location, SNP location,covariates.协变量covariates指的是血型，年龄，性别这些因素。

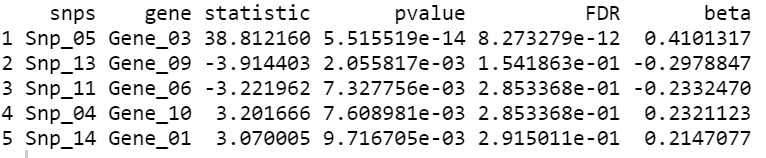
用作者给提供的数据演示，可以得到以下的结果

与癌症相关的研究

因为是想将eQTL的计算方法应用到癌症研究的领域，所以在查找文献时我找到了两篇文献使用这种方法；

第一个是作者使用METABRIC，TCGA，GTEx数据库里面的乳腺癌位点相关的数据做的全基因组关联分析，他做的是顺式的eQTL分析，作者使用的是线性模型，但是没给出一个具体的方式。

而另一篇文献是比较值得借鉴的，作者是用eQTL分析获得乳腺癌的危险位点。在eQTL分析是： $$ T_i = Sc_i+M_i+\epsilon_i\\epsilon_i=G_i+\omega_i $$ $T$是转录丰度；$G$是种系基因型；$Sc$是体细胞拷贝数影响；$M$是启动子区域的CpG甲基化水平。作者的分析策略是：通过多元线性回归去计算$Sc_i$和$M_i$的残差表达式$\epsilon_i$，然后再回归残差表达式到种系基因型$G_i$。

作者通过这种方式来分别估计了遗传决定因素，体细胞copynumber变化，和甲基化水平对转录丰度的影响。