Skip to content

Latest commit

 

History

History
177 lines (142 loc) · 7.9 KB

load-test.md

File metadata and controls

177 lines (142 loc) · 7.9 KB
Raw

Load Testing Aloha Models

As of version 3.3.2-SNAPSHOT, Aloha supports load testing through the command line interface (CLI). This load test functionality is exposed through the modelrunner API in aloha-core. To load test, we recommend using the aloha-cli/bin/aloha-cli script.
An example follows:

Command

cd aloha           # Change to the aloha root directory

mvn clean package  # Build aloha if necessary.

./aloha-cli/bin/aloha-cli \
 -cp $(find $PWD/aloha-cli/target -name "*with*"):$(find $PWD/aloha-core/target -name "*-tests.jar") \
 --modelrunner \
   -p com.eharmony.aloha.test.proto.Testing.UserProto \
   --imports "scala.math._,com.eharmony.aloha.feature.BasicFunctions._" \
   --input-file file://$PWD/aloha-core/src/test/resources/fizz_buzzs.proto \
   --output-file file://$PWD/loadtest-$(date "+%Y%m%d%H%M%S").txt \
                                   \
   --lt-pred-per-loop 1000         \
   --lt-threads 5                  \
   --lt-loops 2000                 \
   --lt-report-loop-multiple 1     \
   --lt-use-score-objects true     \
                                   \
   file://$PWD/aloha-core/src/test/resources/fizzbuzz_proto.json

Parameter Explanations

The aloha-cli requires a classpath argument -cp that contains all of the jars necessary to run the CLI. The first entry one will notice is the aloha-cli-[VERSION]-jar-with-dependencies.jar. This contains the code necessary to run the infrastructure. The second entry is for the jar that has the proto definitions. This is only necessary when specififying the -p option along its argument: the protocol buffer canonical class name whose type is used as the model's domain.

If -p is provided, the input format is expected to be one base64-encoded byte array per line. This is the same as in other CLI use cases.

Like in other CLI use cases one can use the --imports, --input-file, --output-file options. The --imports option--like when creating a CompiledSemantics programmatically--augments the capabilities available to the model feature specifications.

The middle five parameters in the above command, prefixed by --lt- are load test-specific parameters. These include:

  • --lt-pred-per-loop [INT] The number of predictions to make per loop, per thread. If the amount of input data provided is less than this value, then replicate the data to reach the desired number. If the number is amount of input data is greater than this value, truncate the data to this size.
  • --lt-threads [INT] The number of concurrent threads in the load test.
  • --lt-loops [INT] The number of times to loop over dataset that is expanded or pruned to be the size listed in --lt-pred-per-loop.
  • --lt-report-loop-multiple [INT] How often to report the statistics. 1 reports on every loop, 2 on every 2 loops, etc.
  • --lt-use-score-objects [true | false] Whether to use Aloha's more heavyweight score function (true) or the lightweight apply (false) method.

If any of the load test parameters is provided, a load test will be run. In this event, sensible default values for omitted parameters will be used.

Results

If we cat the output file produced from the above command, we get something like the following:

cat loadtest-20160922142518.txt | head 
loop_number	pred_sec	running_pred	running_nonempty_pred	mem_used_mb	mem_unallocated_mb	unixtime_ns
0	Infinity	0	0	142.41931	3498.5806	4834312901301
1	18936.408	5000	5000	201.97498	3439.025	4834577862035
2	50372.32	10000	10000	225.45836	3415.5417	4834677300677
3	92686.39	15000	15000	248.94174	3392.0583	4834731394737
4	102816.56	20000	20000	272.42514	3368.575	4834780174251
5	123596.555	25000	25000	295.90848	3345.0916	4834820794341
6	132132.03	30000	30000	319.3919	3321.6082	4834858794000
7	138070.47	35000	35000	342.87524	3298.1248	4834895184309
8	104266.12	40000	40000	366.35858	3274.6414	4834943322331
...

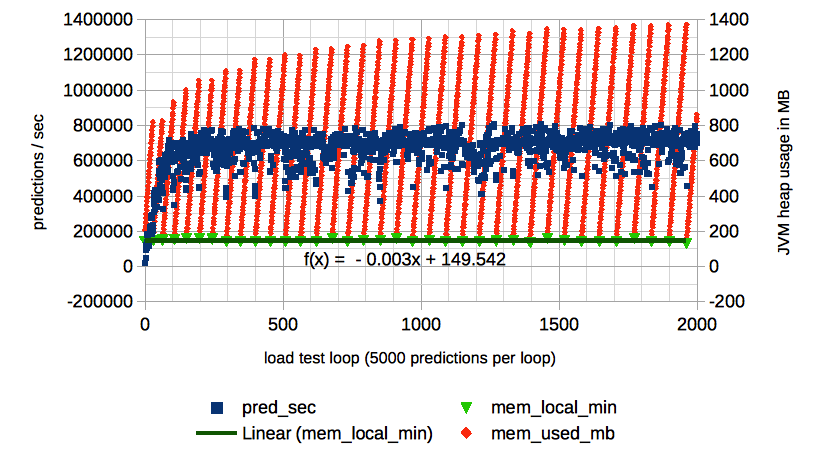
which, when graphed, looks like this:

Load Test Companion

There are a few things this graph shows us. Firstly, the prediction speed (in blue) ramps up over the first 100 or so loops or about 500K predictions. After this, the prediction speed remains relatively constant. The point-wise speed distribution can be computed by taking a sliding sample centered at a given loop number and the quantile statistics can be used to provide confidence bands if so desired.

When analyzing the memory (in red), one should note the regular diagonal stripes. This indicates that memory is increasing until the point where the stripe reaches a local maximum. At this point, memory is garbage collected and the memory drops to a local minimum. Notice the trend of the local maxima. These values appear to be increasing at a roughly logarithmic rate. This is okay and is intimately related to the widening gap between the stripes over time. The increase in local maxima indicates that the maximum memory in use increases between garbage collections. The reason is that garbage collection frequency is decreasing, which can be seen by the widening gap between stripes. The more important characteristic of the memory graph is the trend of the local minima. It's apparent in the graph that the trend line is flat (and even slightly negative). This constant nature is an indication that there are no memory leaks.

To get the local minima data, we can write some quick Scala code that uses a sliding window to find the minima.

// Get loop number and memory data.
val data = 
  io.Source.fromFile("loadtest-20160922142518.txt").
    getLines.
    drop(1).
    map{ l => 
      val a = l.split("\t")
      (a(0).toInt, a(4).toDouble)
    }.toVector

// Find local minima in the middle of the dataset.
val minimaMiddle = 
  data.sliding(3).
    collect { 
      case Vector((_, x),p@(_, y),(_, z)) if x > y && y < z => p
    }.toVector

// Find local minima at ends of data.    
val firstMinimum = data.take(if (data.head._2 < data(1)._2) 1 else 0)
val lastMinimum = data.takeRight(if (data.last._2 < data(data.size - 2)._2) 1 else 0)
val minima = firstMinimum ++ minimaMiddle ++ lastMinimum

// Print the results in TSV format.
minima foreach { case(i, v) => println(s"$i\t$v") }

From these local minima values, we can run a one-sided t-test on the slope of the line determined by an OLS linear regression. This will provide (for a specified significance) whether a memory leak may have occurred. To do this, we run the following:

def getSlopeAndTwoTailedPValue(data: Seq[(Double, Double)]): (Double, Double) = {
  val(xs, ys) = data.unzip

  // Create a linear regression (with intercept).
  val r = new org.apache.commons.math3.stat.regression.SimpleRegression(true)
  r.addObservations(xs.map(x => Array(x)).toArray, ys.toArray)
  (r.getSlope, r.getSignificance)
}

def possibleMemoryLeak(data: Seq[(Double, Double)], alpha: Double = 0.05): Boolean = {
  val (slope, twoTailedPValue) = getSlopeAndTwoTailedPValue(data)

  // http://www.ats.ucla.edu/stat/mult_pkg/faq/general/tail_tests.htm
  val oneTailedPValue = if (slope > 0) twoTailedPValue / 2
                        else           1 - twoTailedPValue / 2

  oneTailedPValue < alpha
}

We turn the two-tailed p-value into a one-tailed p-value for the case that β > 0 and compared it α to determine whether the null hypothesis that β ≤ 0 should be rejected.

Notice in the above graph, that since the slope is negative (-0.003) and the two-sided p-value is 0.117, we can't reject the null hypothesis at a significance level α = 0.05 because 1 - 0.117 / 2 > 0.05. So we can't say with significance that a memory leak occurred.