README.md

题目描述: 腐烂的橘子

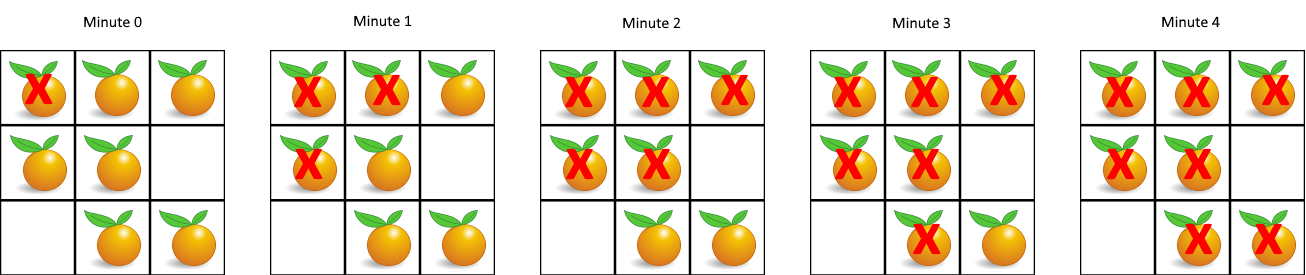
在给定的网格中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。 每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

示例 1:

输入：[[2,1,1],[1,1,0],[0,1,1]]
输出：4

解题思路:

广度优先搜索:

利用模拟队列实现

首先先找出已经感染的橘子，也就是time == 0时候，将这些橘子入队，然后每次取出队头的感染橘子，对其四周进行感染，这里要注意的是数组的越界判断。

最后当队空时进行判断，如果grid中还有新鲜橘子，那么感染失败，返回-1，否则返回最后出队的橘子的time。

时间复杂度：

O(mn)

空间复杂度

O(mn)

代码

C++:

BFS

class Solution {
public:
    int orangesRotting(vector<vector<int>>& grid) {
        int res = 0;
        if (grid.empty()) return res;
        vector<int> dx (4,0);
        vector<int> dy (4,0);
        dx[0]=1;
        dx[1]=-1;
        dy[2]=1;
        dy[3]=-1;
        queue<pair<int,int>> q; // pair的用法,将2个数据组合成一个数据，当需要这样的需求时就可以使用pair，如stl中的map就是将key和value放在一起来保存
        int m = grid.size();
        int n = grid[0].size();
        // 把腐烂的🍊加入队列中，作为开始扩散的起点
        for (int i=0;i<m;i++)
        {
            for (int j=0;j<n;j++)
            {
                if (grid[i][j]==2)
                {
                    q.push(make_pair(i,j));
                }
            }
        }
        //从腐烂的🍊开始感染，其实就是一个bfs求无权图最短路的问题
        while(!q.empty())
        {
            int size = q.size(); // 感染🍊的上下左右算一层
            for (int i=0;i<size;i++)
            {
                pair<int,int> d = q.front();
                q.pop();
                for (int k=0;k<4;k++)
                {
                    int x = d.first + dx[k];
                    int y = d.second + dy[k];
                    if (x>=0 && x<m && y>=0 && y<n && grid[x][y]==1)
                    {
                        grid[x][y]=2;
                        q.push(make_pair(x,y));
                    }
                }
            }
            if (!q.empty()) res++;
        }
        //遍历矩阵，判断是否有🍊还未被感染，也就是是否还有grid[i][j] = 1的地儿
        for (int i=0;i<m;i++)
        {
            for (int j=0;j<n;j++)
            {
                if (grid[i][j]==1)
                    return -1;
            }
        }
        // for(auto row : grid) 
        // {
        //     for (int i : row)
        //         if (i == 1) return -1;
        // }
        return res;
    }
};

Python:

BFS

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        res = 0
        if grid == []:
            return res
        m = len(grid)
        n = len(grid[0])
        dx = [1,-1,0,0]
        dy = [0,0,1,-1]
        q=[]
        for i in range(m):
            for j in range(n):
                if grid[i][j]==2:
                    q.append((i,j))
        while q:
            size = len(q)
            for i in range(size):
                d = q.pop(0)
                for k in range(4):
                    x = d[0] + dx[k]
                    y = d[1] + dy[k]
                    if 0<=x<m and 0<=y<n and grid[x][y]==1:
                        grid[x][y]=2
                        q.append((x,y))
            if q:
                res+=1
        for row in grid:
            for i in row:
                if i==1:
                    return -1
        return res

参考

• 题解