README.md

题目描述: 621. 任务调度器

给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间，CPU 可以完成一个任务，或者处于待命状态。

然而，两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的 最短时间 。

示例 :

输入：tasks = ["A","A","A","B","B","B"], n = 2
输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B
     在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。
     
     
输入：tasks = ["A","A","A","B","B","B"], n = 0
输出：6
解释：在这种情况下，任何大小为 6 的排列都可以满足要求，因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类

输入：tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出：16
解释：一种可能的解决方案是：
     A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A

解题思路:

桶思想

• 记录最大任务数量 N，看一下任务数量并列最多的任务有多少个，即最后一个桶子的任务数 X，计算 NUM1=(N-1)*(n+1)+x
• NUM2=tasks.size()

输出其中较大值即可

因为存在空闲时间时肯定是 NUM1 大，不存在空闲时间时肯定是 NUM2>=NUM1

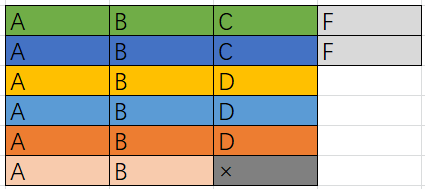
如下图所示：

桶大小是n+1, 临时扩充一些桶。其实就是没有冷却时间了，执行任务所需的时间，就是任务的数量

时间复杂度：

O(nlogn)

空间复杂度

O(1)

代码

class Solution {
public:
    int leastInterval(vector<char>& tasks, int n) {
        int res = 0;
        vector<int> m(26);
        for (char &c : tasks) {
            m[c -'A']++;
        }
        sort(m.begin(), m.end(), cmp);
        int cnt = 1; // 最后一桶的任务数量，先初始设置为1
        while (cnt < m.size() && m[cnt] == m[0]) {
            cnt++;
        }
        res = max(cnt+(n+1)*(m[0]-1), (int)tasks.size());
        return res;
    }
    static bool cmp(int &a , int &b) {
        return a > b;
    }
};