P1003.cpp

#include <cstdio>

using namespace std;

struct Carpet // (x,y,w,h)表示一张地毯
{
    int serial; // 编号，同时也能表示地毯的覆盖关系
    int x;
    int y;
    int w; // 宽
    int h; // 高
};

int main()
{
    int n; // n张地毯
    scanf("%d", &n);
    Carpet carpets[n]; // 储存所有地毯
    for (int i = 0; i < n; i++)
    {                              // 读入地毯数据
        carpets[i].serial = i + 1; // 给地毯编号
        scanf("%d %d %d %d", &carpets[i].x, &carpets[i].y, &carpets[i].w, &carpets[i].h);
    }
    int x, y;
    scanf("%d %d", &x, &y);
    int target = -1; // (x,y)点最上层的地毯编号
    for (int i = 0; i < n; i++)
    {
        if (carpets[i].x > x || carpets[i].y > y) // 左下角坐标不在(x,y)内，看都不用看
            continue;
        if (x <= carpets[i].x + carpets[i].w && y <= carpets[i].y + carpets[i].h && carpets[i].serial > target) // 如果这块地毯包括了点(x,y)，且覆盖在上层
            target = carpets[i].serial;
    }
    printf("%d", target);
    return 0;
}

/*
    这题是简单的几何计算，判断一个点是否被地毯覆盖，只需要判断这个点有没有被某张地毯的四个边界包在其中即可。

        - SomeBottle 2023.3.8
*/

/*
# [NOIP2011 提高组] 铺地毯

## 题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 $n$ 张地毯，编号从 $1$ 到 $n$。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

## 输入格式

输入共 $n + 2$ 行。

第一行，一个整数 $n$，表示总共有 $n$ 张地毯。

接下来的 $n$ 行中，第 $i+1$ 行表示编号 $i$ 的地毯的信息，包含四个整数 $a ,b ,g ,k$，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标 $(a, b)$ 以及地毯在 $x$ 轴和 $y$ 轴方向的长度。

第 $n + 2$ 行包含两个整数 $x$ 和 $y$，表示所求的地面的点的坐标 $(x, y)$。

## 输出格式

输出共 $1$ 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出 `-1`。

## 样例 #1

### 样例输入 #1

```
3
1 0 2 3
0 2 3 3
2 1 3 3
2 2
```

### 样例输出 #1

```
3
```

## 样例 #2

### 样例输入 #2

```
3
1 0 2 3
0 2 3 3
2 1 3 3
4 5
```

### 样例输出 #2

```
-1
```

## 提示

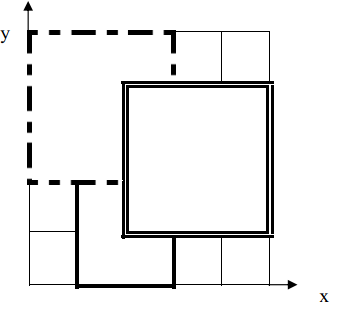
【样例解释 1】

如下图，$1$ 号地毯用实线表示，$2$ 号地毯用虚线表示，$3$ 号用双实线表示，覆盖点 $(2,2)$ 的最上面一张地毯是 $3$ 号地毯。

 ![](https://cdn.luogu.com.cn/upload/pic/100.png)

【数据范围】

对于 $30\%$ 的数据，有 $n \le 2$。
对于 $50\%$ 的数据，$0 \le a, b, g, k \le 100$。
对于 $100\%$ 的数据，有 $0 \le n \le 10^4$, $0 \le a, b, g, k \le {10}^5$。

noip2011 提高组 day1 第 $1$ 题。
*/