-
Notifications
You must be signed in to change notification settings - Fork 201
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Cahill-Concialdi conformal projection? #173
Comments
|
I think the Cahill-Concialdi would be a great addition! |
|
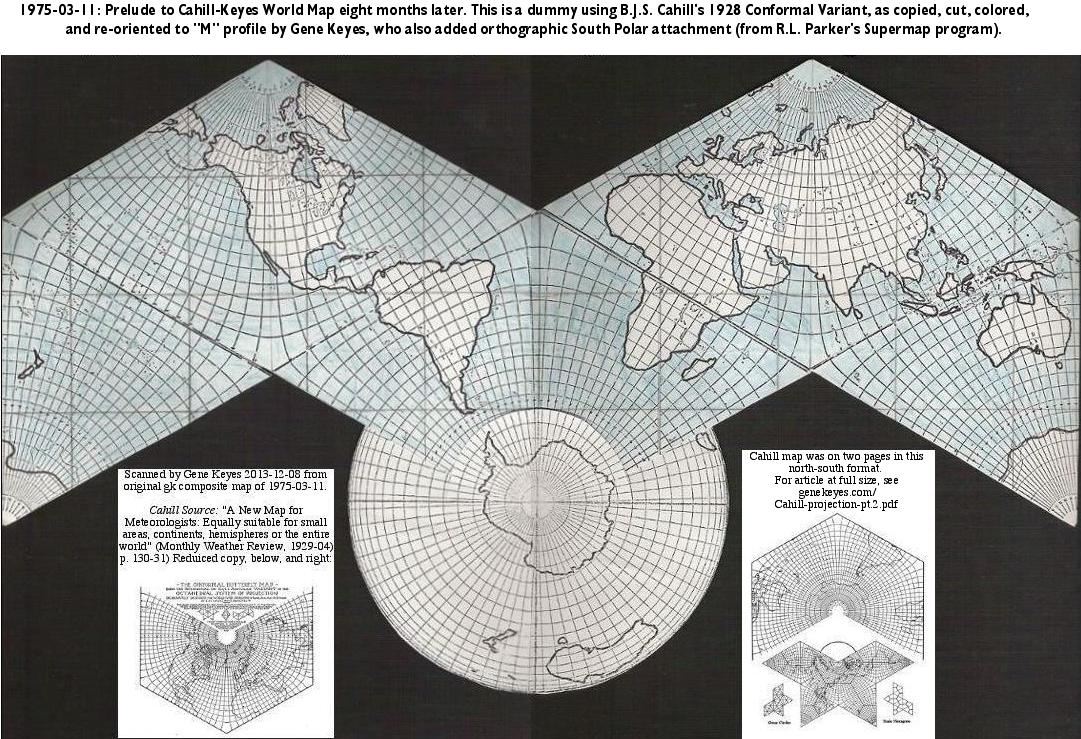
As TJung1968 mentioned above, for more details on the Cahill Conformal and its derivatives by Gene Keyes, and Jacob Rus, see http://www.genekeyes.com/CAHILL-VARIANTS/Cahill-Conformal.html I did indeed xerox the Oscar Adams tables in 1983 at the Cahill Archives in the Bancroft Library, U.Cal.Berkeley, but the copies' legibility was very poor. However, I think the Conformal neo-Cahill remake by Jacob Rus [i.e., in a Cahill-Keyes frame] is superior, for all the reasons I've been propounding since 1975: http://www.genekeyes.com/Redesigning-Cahill.html The C-K is not conformal, but has a hand-calculated graticule of "proportional geocells". Its precursor came about when I began to re-arrange Cahill's 1928 Conformal Butterfly Variant: |
|
(I've updated the reference image because the previous one had somehow disappeared.) |
|
@jkunimune15 has a Java implementation of the Cahill-Concialdi projection and I was able to port the forward projection code into JavaScript (though not the inverse projection). |
|
Here's a really nice variant I found on the website of @cahill-keyes : |

Refs:
The text was updated successfully, but these errors were encountered: