README.md

441. 排列硬币

English Version

题目描述

你总共有 n 枚硬币，并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯，其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。

给你一个数字 n ，计算并返回可形成 完整阶梯行 的总行数。

 

示例 1：

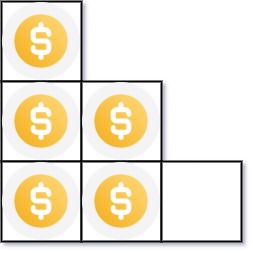
输入：n = 5
输出：2
解释：因为第三行不完整，所以返回 2 。

示例 2：

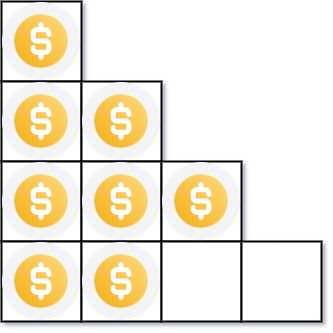
输入：n = 8
输出：3
解释：因为第四行不完整，所以返回 3 。

 

提示：

• 1 <= n <= 231 - 1

解法

方法一：数学推导

(1 + x) * x / 2 <= n，求解 x。

(x + 1/2)² <= 2n + 1/4，即 x <= sqrt(2n + 1/4) - 1/2。

由于 2n 可能溢出，故转换为 x <= sqrt(2) * sqrt(n + 1/8) - 1/2。

class Solution:
    def arrangeCoins(self, n: int) -> int:
        return int(math.sqrt(2) * math.sqrt(n + 0.125) - 0.5)

class Solution {
    public int arrangeCoins(int n) {
        return (int) (Math.sqrt(2) * Math.sqrt(n + 0.125) - 0.5);
    }
}

using LL = long;

class Solution {
public:
    int arrangeCoins(int n) {
        LL left = 1, right = n;
        while (left < right) {
            LL mid = left + right + 1 >> 1;
            LL s = (1 + mid) * mid >> 1;
            if (n < s)
                right = mid - 1;
            else
                left = mid;
        }
        return left;
    }
};

func arrangeCoins(n int) int {
	left, right := 1, n
	for left < right {
		mid := (left + right + 1) >> 1
		if (1+mid)*mid/2 <= n {
			left = mid
		} else {
			right = mid - 1
		}
	}
	return left
}

方法二：二分查找

class Solution:
    def arrangeCoins(self, n: int) -> int:
        left, right = 1, n
        while left < right:
            mid = (left + right + 1) >> 1
            if (1 + mid) * mid // 2 <= n:
                left = mid
            else:
                right = mid - 1
        return left

class Solution {
    public int arrangeCoins(int n) {
        long left = 1, right = n;
        while (left < right) {
            long mid = (left + right + 1) >>> 1;
            if ((1 + mid) * mid / 2 <= n) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return (int) left;
    }
}