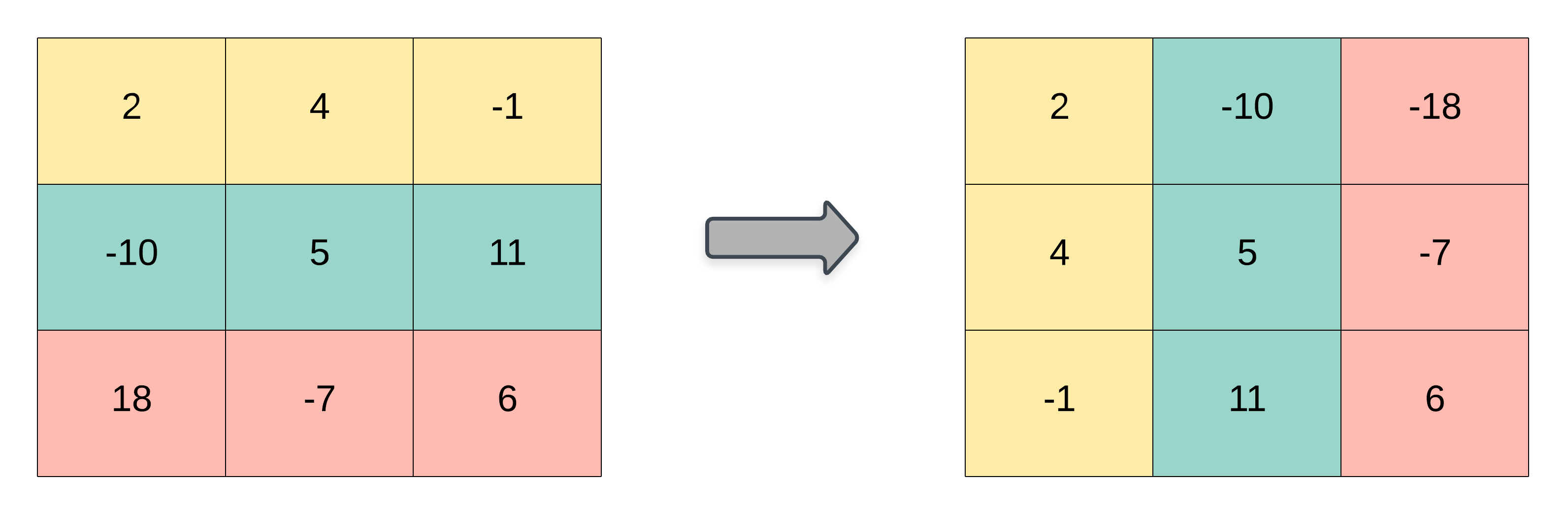
Given a 2D integer array matrix, return the transpose of matrix.
The transpose of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
Example 1:
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[1,4,7],[2,5,8],[3,6,9]]
Example 2:
Input: matrix = [[1,2,3],[4,5,6]] Output: [[1,4],[2,5],[3,6]]
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10001 <= m * n <= 105-109 <= matrix[i][j] <= 109
class Solution:
def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
return list(zip(*matrix))class Solution {
public int[][] transpose(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int[][] ans = new int[n][m];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
ans[i][j] = matrix[j][i];
}
}
return ans;
}
}class Solution {
public:
vector<vector<int>> transpose(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> ans(n, vector<int>(m));
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
ans[i][j] = matrix[j][i];
return ans;
}
};func transpose(matrix [][]int) [][]int {
m, n := len(matrix), len(matrix[0])
ans := make([][]int, n)
for i := range ans {
ans[i] = make([]int, m)
for j := range ans[i] {
ans[i][j] = matrix[j][i]
}
}
return ans
}/**
* @param {number[][]} matrix
* @return {number[][]}
*/
var transpose = function (matrix) {
const m = matrix.length;
const n = matrix[0].length;
const ans = new Array(n).fill(0).map(() => new Array(m).fill(0));
for (let i = 0; i < n; ++i) {
for (let j = 0; j < m; ++j) {
ans[i][j] = matrix[j][i];
}
}
return ans;
};