给你二叉树的根结点 root ,请你设计算法计算二叉树的 垂序遍历 序列。
对位于 (row, col) 的每个结点而言,其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。
二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束,按列索引每一列上的所有结点,形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点,则按结点的值从小到大进行排序。
返回二叉树的 垂序遍历 序列。
示例 1:
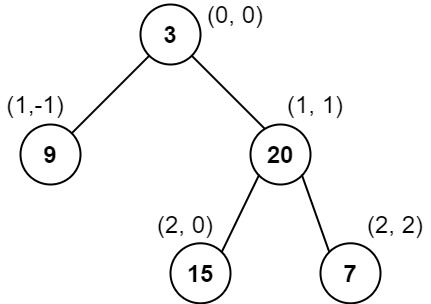
输入:root = [3,9,20,null,null,15,7] 输出:[[9],[3,15],[20],[7]] 解释: 列 -1 :只有结点 9 在此列中。 列 0 :只有结点 3 和 15 在此列中,按从上到下顺序。 列 1 :只有结点 20 在此列中。 列 2 :只有结点 7 在此列中。
示例 2:
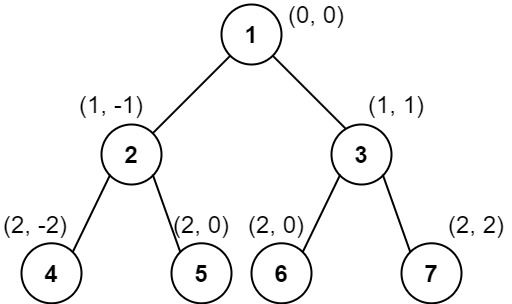
输入:root = [1,2,3,4,5,6,7]
输出:[[4],[2],[1,5,6],[3],[7]]
解释:
列 -2 :只有结点 4 在此列中。
列 -1 :只有结点 2 在此列中。
列 0 :结点 1 、5 和 6 都在此列中。
1 在上面,所以它出现在前面。
5 和 6 位置都是 (2, 0) ,所以按值从小到大排序,5 在 6 的前面。
列 1 :只有结点 3 在此列中。
列 2 :只有结点 7 在此列中。
示例 3:
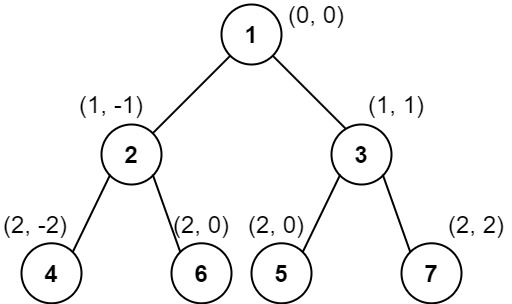
输入:root = [1,2,3,4,6,5,7] 输出:[[4],[2],[1,5,6],[3],[7]] 解释: 这个示例实际上与示例 2 完全相同,只是结点 5 和 6 在树中的位置发生了交换。 因为 5 和 6 的位置仍然相同,所以答案保持不变,仍然按值从小到大排序。
提示:
- 树中结点数目总数在范围
[1, 1000]内 0 <= Node.val <= 1000
我们设计一个函数
接着,我们遍历
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def verticalTraversal(self, root: Optional[TreeNode]) -> List[List[int]]:
def dfs(root: Optional[TreeNode], i: int, j: int):
if root is None:
return
nodes.append((j, i, root.val))
dfs(root.left, i + 1, j - 1)
dfs(root.right, i + 1, j + 1)
nodes = []
dfs(root, 0, 0)
nodes.sort()
ans = []
prev = -2000
for j, _, val in nodes:
if prev != j:
ans.append([])
prev = j
ans[-1].append(val)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private List<int[]> nodes = new ArrayList<>();
public List<List<Integer>> verticalTraversal(TreeNode root) {
dfs(root, 0, 0);
Collections.sort(nodes, (a, b) -> {
if (a[0] != b[0]) {
return Integer.compare(a[0], b[0]);
}
if (a[1] != b[1]) {
return Integer.compare(a[1], b[1]);
}
return Integer.compare(a[2], b[2]);
});
List<List<Integer>> ans = new ArrayList<>();
int prev = -2000;
for (int[] node : nodes) {
int j = node[0], val = node[2];
if (prev != j) {
ans.add(new ArrayList<>());
prev = j;
}
ans.get(ans.size() - 1).add(val);
}
return ans;
}
private void dfs(TreeNode root, int i, int j) {
if (root == null) {
return;
}
nodes.add(new int[] {j, i, root.val});
dfs(root.left, i + 1, j - 1);
dfs(root.right, i + 1, j + 1);
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> verticalTraversal(TreeNode* root) {
vector<tuple<int, int, int>> nodes;
function<void(TreeNode*, int, int)> dfs = [&](TreeNode* root, int i, int j) {
if (!root) {
return;
}
nodes.emplace_back(j, i, root->val);
dfs(root->left, i + 1, j - 1);
dfs(root->right, i + 1, j + 1);
};
dfs(root, 0, 0);
sort(nodes.begin(), nodes.end());
vector<vector<int>> ans;
int prev = -2000;
for (auto [j, _, val] : nodes) {
if (j != prev) {
prev = j;
ans.emplace_back();
}
ans.back().push_back(val);
}
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func verticalTraversal(root *TreeNode) (ans [][]int) {
nodes := [][3]int{}
var dfs func(*TreeNode, int, int)
dfs = func(root *TreeNode, i, j int) {
if root == nil {
return
}
nodes = append(nodes, [3]int{j, i, root.Val})
dfs(root.Left, i+1, j-1)
dfs(root.Right, i+1, j+1)
}
dfs(root, 0, 0)
sort.Slice(nodes, func(i, j int) bool {
a, b := nodes[i], nodes[j]
return a[0] < b[0] || a[0] == b[0] && (a[1] < b[1] || a[1] == b[1] && a[2] < b[2])
})
prev := -2000
for _, node := range nodes {
j, val := node[0], node[2]
if j != prev {
ans = append(ans, nil)
prev = j
}
ans[len(ans)-1] = append(ans[len(ans)-1], val)
}
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function verticalTraversal(root: TreeNode | null): number[][] {
const nodes: [number, number, number][] = [];
const dfs = (root: TreeNode | null, i: number, j: number) => {
if (!root) {
return;
}
nodes.push([j, i, root.val]);
dfs(root.left, i + 1, j - 1);
dfs(root.right, i + 1, j + 1);
};
dfs(root, 0, 0);
nodes.sort((a, b) => a[0] - b[0] || a[1] - b[1] || a[2] - b[2]);
const ans: number[][] = [];
let prev = -2000;
for (const [j, _, val] of nodes) {
if (j !== prev) {
prev = j;
ans.push([]);
}
ans.at(-1)!.push(val);
}
return ans;
}