Skip to content

Latest commit

 

History

History
679 lines (615 loc) · 18.3 KB

README.md

File metadata and controls

679 lines (615 loc) · 18.3 KB
Raw

1020. 飞地的数量

English Version

题目描述

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

 

示例 1：

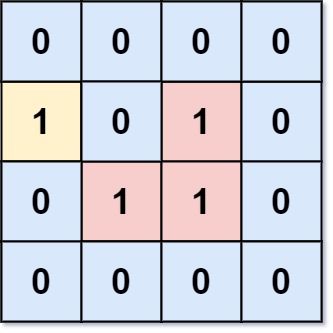
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

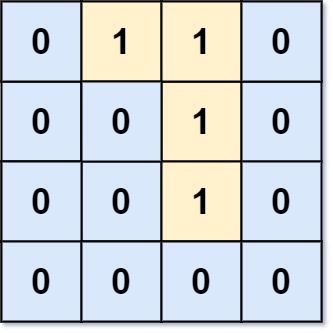
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

 

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 500
  • grid[i][j] 的值为 0 或 1

解法

方法一：DFS

我们可以从边界上的陆地开始进行深度优先搜索，将所有与边界相连的陆地都标记为 $0$。最后，统计剩余的 $1$ 的个数，即为答案。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数。

class Solution:
    def numEnclaves(self, grid: List[List[int]]) -> int:
        def dfs(i, j):
            grid[i][j] = 0
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y]:
                    dfs(x, y)

        m, n = len(grid), len(grid[0])
        dirs = (-1, 0, 1, 0, -1)
        for i in range(m):
            for j in range(n):
                if grid[i][j] and (i == 0 or i == m - 1 or j == 0 or j == n - 1):
                    dfs(i, j)
        return sum(v for row in grid for v in row)
class Solution {
    private int m;
    private int n;
    private int[][] grid;

    public int numEnclaves(int[][] grid) {
        this.grid = grid;
        m = grid.length;
        n = grid[0].length;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1 && (i == 0 || i == m - 1 || j == 0 || j == n - 1)) {
                    dfs(i, j);
                }
            }
        }
        int ans = 0;
        for (var row : grid) {
            for (var v : row) {
                ans += v;
            }
        }
        return ans;
    }

    private void dfs(int i, int j) {
        grid[i][j] = 0;
        int[] dirs = {-1, 0, 1, 0, -1};
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                dfs(x, y);
            }
        }
    }
}
class Solution {
public:
    int numEnclaves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int dirs[5] = {-1, 0, 1, 0, -1};
        function<void(int, int)> dfs = [&](int i, int j) {
            grid[i][j] = 0;
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]) {
                    dfs(x, y);
                }
            }
        };
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] && (i == 0 || i == m - 1 || j == 0 || j == n - 1)) {
                    dfs(i, j);
                }
            }
        }
        int ans = 0;
        for (auto& row : grid) {
            for (auto& v : row) {
                ans += v;
            }
        }
        return ans;
    }
};
func numEnclaves(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	dirs := [5]int{-1, 0, 1, 0, -1}
	var dfs func(i, j int)
	dfs = func(i, j int) {
		grid[i][j] = 0
		for k := 0; k < 4; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
				dfs(x, y)
			}
		}
	}
	for i, row := range grid {
		for j, v := range row {
			if v == 1 && (i == 0 || i == m-1 || j == 0 || j == n-1) {
				dfs(i, j)
			}
		}
	}
	for _, row := range grid {
		for _, v := range row {
			ans += v
		}
	}
	return
}
function numEnclaves(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const dirs = [-1, 0, 1, 0, -1];
    const dfs = (i: number, j: number) => {
        grid[i][j] = 0;
        for (let k = 0; k < 4; ++k) {
            const x = i + dirs[k];
            const y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y <= n && grid[x][y] === 1) {
                dfs(x, y);
            }
        }
    };
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] === 1 && (i === 0 || i === m - 1 || j === 0 || j === n - 1)) {
                dfs(i, j);
            }
        }
    }
    let ans = 0;
    for (const row of grid) {
        for (const v of row) {
            ans += v;
        }
    }
    return ans;
}
impl Solution {
    fn dfs(grid: &mut Vec<Vec<i32>>, y: usize, x: usize) {
        if y >= grid.len() || x >= grid[0].len() || grid[y][x] == 0 {
            return;
        }
        grid[y][x] = 0;
        Solution::dfs(grid, y + 1, x);
        Solution::dfs(grid, y, x + 1);
        if y != 0 {
            Solution::dfs(grid, y - 1, x);
        }
        if x != 0 {
            Solution::dfs(grid, y, x - 1);
        }
    }
    pub fn num_enclaves(mut grid: Vec<Vec<i32>>) -> i32 {
        let mut res = 0;
        let m = grid.len();
        let n = grid[0].len();
        for i in 0..m {
            Solution::dfs(&mut grid, i, 0);
            Solution::dfs(&mut grid, i, n - 1);
        }
        for i in 0..n {
            Solution::dfs(&mut grid, 0, i);
            Solution::dfs(&mut grid, m - 1, i);
        }
        for i in 1..m - 1 {
            for j in 1..n - 1 {
                if grid[i][j] == 1 {
                    res += 1;
                }
            }
        }
        res
    }
}

方法二：BFS

我们也可以使用广度优先搜索的方法，将边界上的陆地入队，然后进行广度优先搜索，将所有与边界相连的陆地都标记为 $0$。最后，统计剩余的 $1$ 的个数，即为答案。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数。

class Solution:
    def numEnclaves(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        q = deque()
        for i in range(m):
            for j in range(n):
                if grid[i][j] and (i == 0 or i == m - 1 or j == 0 or j == n - 1):
                    q.append((i, j))
                    grid[i][j] = 0
        dirs = (-1, 0, 1, 0, -1)
        while q:
            i, j = q.popleft()
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if x >= 0 and x < m and y >= 0 and y < n and grid[x][y]:
                    q.append((x, y))
                    grid[x][y] = 0
        return sum(v for row in grid for v in row)
class Solution {
    public int numEnclaves(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        Deque<int[]> q = new ArrayDeque<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1 && (i == 0 || i == m - 1 || j == 0 || j == n - 1)) {
                    q.offer(new int[] {i, j});
                    grid[i][j] = 0;
                }
            }
        }
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            var p = q.poll();
            for (int k = 0; k < 4; ++k) {
                int x = p[0] + dirs[k], y = p[1] + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                    q.offer(new int[] {x, y});
                    grid[x][y] = 0;
                }
            }
        }
        int ans = 0;
        for (var row : grid) {
            for (var v : row) {
                ans += v;
            }
        }
        return ans;
    }
}
class Solution {
public:
    int numEnclaves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int dirs[5] = {-1, 0, 1, 0, -1};
        queue<pair<int, int>> q;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] && (i == 0 || i == m - 1 || j == 0 || j == n - 1)) {
                    q.emplace(i, j);
                    grid[i][j] = 0;
                }
            }
        }
        while (!q.empty()) {
            auto [i, j] = q.front();
            q.pop();
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]) {
                    q.emplace(x, y);
                    grid[x][y] = 0;
                }
            }
        }
        int ans = 0;
        for (auto& row : grid) {
            for (auto& v : row) {
                ans += v;
            }
        }
        return ans;
    }
};
func numEnclaves(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	dirs := [5]int{-1, 0, 1, 0, -1}
	q := [][2]int{}
	for i, row := range grid {
		for j, v := range row {
			if v == 1 && (i == 0 || i == m-1 || j == 0 || j == n-1) {
				q = append(q, [2]int{i, j})
				grid[i][j] = 0
			}
		}
	}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		for k := 0; k < 4; k++ {
			x, y := p[0]+dirs[k], p[1]+dirs[k+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
				q = append(q, [2]int{x, y})
				grid[x][y] = 0
			}
		}
	}
	for _, row := range grid {
		for _, v := range row {
			ans += v
		}
	}
	return
}
function numEnclaves(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const dirs = [-1, 0, 1, 0, -1];
    const q: number[][] = [];
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] === 1 && (i === 0 || i === m - 1 || j === 0 || j === n - 1)) {
                q.push([i, j]);
                grid[i][j] = 0;
            }
        }
    }
    while (q.length) {
        const [i, j] = q.shift()!;
        for (let k = 0; k < 4; ++k) {
            const x = i + dirs[k];
            const y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y <= n && grid[x][y] === 1) {
                q.push([x, y]);
                grid[x][y] = 0;
            }
        }
    }
    let ans = 0;
    for (const row of grid) {
        for (const v of row) {
            ans += v;
        }
    }
    return ans;
}

方法三：并查集

我们还可以利用并查集的方法，将边界上的陆地与一个虚拟的节点 $(m, n)$ 进行合并，然后遍历矩阵中的所有陆地，将其与上下左右的陆地进行合并。最后，统计所有与虚拟节点 $(m, n)$ 不连通的陆地的个数，即为答案。

时间复杂度 $O(m \times n \alpha(m \times n))$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数，而 $\alpha$ 为 阿克曼函数 的反函数。

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.size = [1] * n

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa != pb:
            if self.size[pa] > self.size[pb]:
                self.p[pb] = pa
                self.size[pa] += self.size[pb]
            else:
                self.p[pa] = pb
                self.size[pb] += self.size[pa]


class Solution:
    def numEnclaves(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        uf = UnionFind(m * n + 1)
        dirs = (-1, 0, 1, 0, -1)
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                if v:
                    if i == 0 or i == m - 1 or j == 0 or j == n - 1:
                        uf.union(i * n + j, m * n)
                    else:
                        for a, b in pairwise(dirs):
                            x, y = i + a, j + b
                            if x >= 0 and x < m and y >= 0 and y < n and grid[x][y]:
                                uf.union(i * n + j, x * n + y)
        return sum(
            grid[i][j] == 1 and uf.find(i * n + j) != uf.find(m * n)
            for i in range(m)
            for j in range(n)
        )
class UnionFind {
    private int[] p;
    private int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
            size[i] = 1;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public void union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            if (size[pa] > size[pb]) {
                p[pb] = pa;
                size[pa] += size[pb];
            } else {
                p[pa] = pb;
                size[pb] += size[pa];
            }
        }
    }
}

class Solution {
    public int numEnclaves(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        UnionFind uf = new UnionFind(m * n + 1);
        int[] dirs = {-1, 0, 1, 0, -1};
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                        uf.union(i * n + j, m * n);
                    } else {
                        for (int k = 0; k < 4; ++k) {
                            int x = i + dirs[k], y = j + dirs[k + 1];
                            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                                uf.union(i * n + j, x * n + y);
                            }
                        }
                    }
                }
            }
        }
        int ans = 0;
        for (int i = 1; i < m - 1; ++i) {
            for (int j = 1; j < n - 1; ++j) {
                if (grid[i][j] == 1 && uf.find(i * n + j) != uf.find(m * n)) {
                    ++ans;
                }
            }
        }
        return ans;
    }
}
class UnionFind {
public:
    UnionFind(int n) {
        p = vector<int>(n);
        size = vector<int>(n, 1);
        iota(p.begin(), p.end(), 0);
    }

    void unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            if (size[pa] > size[pb]) {
                p[pb] = pa;
                size[pa] += size[pb];
            } else {
                p[pa] = pb;
                size[pb] += size[pa];
            }
        }
    }

    int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

private:
    vector<int> p, size;
};

class Solution {
public:
    int numEnclaves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        UnionFind uf(m * n + 1);
        int dirs[5] = {-1, 0, 1, 0, -1};
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                        uf.unite(i * n + j, m * n);
                    } else {
                        for (int k = 0; k < 4; ++k) {
                            int x = i + dirs[k], y = j + dirs[k + 1];
                            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                                uf.unite(i * n + j, x * n + y);
                            }
                        }
                    }
                }
            }
        }
        int ans = 0;
        for (int i = 1; i < m - 1; ++i) {
            for (int j = 1; j < n - 1; ++j) {
                ans += grid[i][j] == 1 && uf.find(i * n + j) != uf.find(m * n);
            }
        }
        return ans;
    }
};
type unionFind struct {
	p, size []int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	size := make([]int, n)
	for i := range p {
		p[i] = i
		size[i] = 1
	}
	return &unionFind{p, size}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) {
	pa, pb := uf.find(a), uf.find(b)
	if pa != pb {
		if uf.size[pa] > uf.size[pb] {
			uf.p[pb] = pa
			uf.size[pa] += uf.size[pb]
		} else {
			uf.p[pa] = pb
			uf.size[pb] += uf.size[pa]
		}
	}
}

func numEnclaves(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	uf := newUnionFind(m*n + 1)
	dirs := [5]int{-1, 0, 1, 0, -1}
	for i, row := range grid {
		for j, v := range row {
			if v == 1 {
				if i == 0 || i == m-1 || j == 0 || j == n-1 {
					uf.union(i*n+j, m*n)
				} else {
					for k := 0; k < 4; k++ {
						x, y := i+dirs[k], j+dirs[k+1]
						if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
							uf.union(i*n+j, x*n+y)
						}
					}
				}
			}
		}
	}
	for i, row := range grid {
		for j, v := range row {
			if v == 1 && uf.find(i*n+j) != uf.find(m*n) {
				ans++
			}
		}
	}
	return
}