给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。
二进制矩阵中的 畅通路径 是一条从 左上角 单元格(即,(0, 0))到 右下角 单元格(即,(n - 1, n - 1))的路径,该路径同时满足下述要求:
- 路径途经的所有单元格的值都是
0。 - 路径中所有相邻的单元格应当在 8 个方向之一 上连通(即,相邻两单元之间彼此不同且共享一条边或者一个角)。
畅通路径的长度 是该路径途经的单元格总数。
示例 1:
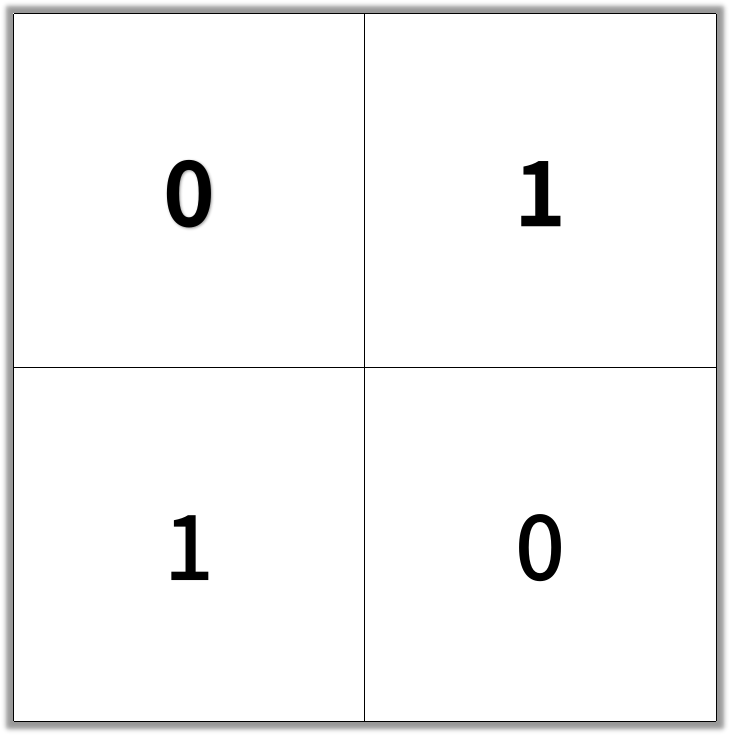
输入:grid = [[0,1],[1,0]] 输出:2
示例 2:
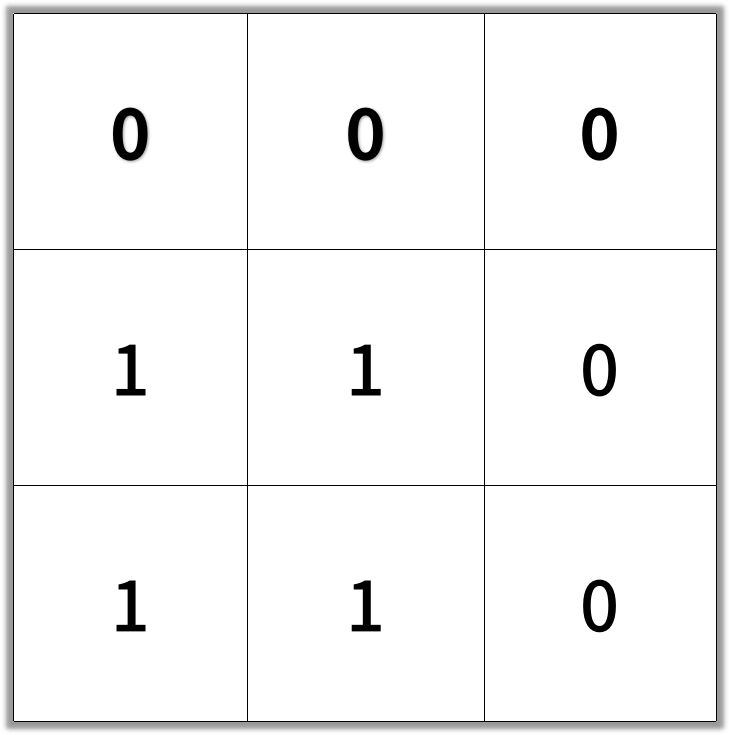
输入:grid = [[0,0,0],[1,1,0],[1,1,0]] 输出:4
示例 3:
输入:grid = [[1,0,0],[1,1,0],[1,1,0]] 输出:-1
提示:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j]为0或1
根据题目描述,一条畅通路径是从左上角单元格
因此,如果左上角单元格
否则,我们创建一个队列
在每一轮搜索中,我们每次取出队首节点
如果在搜索结束后,我们仍然没有到达右下角的节点,那么说明右下角的节点不可达,返回
时间复杂度
class Solution:
def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
if grid[0][0]:
return -1
n = len(grid)
grid[0][0] = 1
q = deque([(0, 0)])
ans = 1
while q:
for _ in range(len(q)):
i, j = q.popleft()
if i == j == n - 1:
return ans
for x in range(i - 1, i + 2):
for y in range(j - 1, j + 2):
if 0 <= x < n and 0 <= y < n and grid[x][y] == 0:
grid[x][y] = 1
q.append((x, y))
ans += 1
return -1class Solution {
public int shortestPathBinaryMatrix(int[][] grid) {
if (grid[0][0] == 1) {
return -1;
}
int n = grid.length;
grid[0][0] = 1;
Deque<int[]> q = new ArrayDeque<>();
q.offer(new int[] {0, 0});
for (int ans = 1; !q.isEmpty(); ++ans) {
for (int k = q.size(); k > 0; --k) {
var p = q.poll();
int i = p[0], j = p[1];
if (i == n - 1 && j == n - 1) {
return ans;
}
for (int x = i - 1; x <= i + 1; ++x) {
for (int y = j - 1; y <= j + 1; ++y) {
if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0) {
grid[x][y] = 1;
q.offer(new int[] {x, y});
}
}
}
}
}
return -1;
}
}class Solution {
public:
int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
if (grid[0][0]) {
return -1;
}
int n = grid.size();
grid[0][0] = 1;
queue<pair<int, int>> q;
q.emplace(0, 0);
for (int ans = 1; !q.empty(); ++ans) {
for (int k = q.size(); k; --k) {
auto [i, j] = q.front();
q.pop();
if (i == n - 1 && j == n - 1) {
return ans;
}
for (int x = i - 1; x <= i + 1; ++x) {
for (int y = j - 1; y <= j + 1; ++y) {
if (x >= 0 && x < n && y >= 0 && y < n && !grid[x][y]) {
grid[x][y] = 1;
q.emplace(x, y);
}
}
}
}
}
return -1;
}
};func shortestPathBinaryMatrix(grid [][]int) int {
if grid[0][0] == 1 {
return -1
}
n := len(grid)
grid[0][0] = 1
q := [][2]int{{0, 0}}
for ans := 1; len(q) > 0; ans++ {
for k := len(q); k > 0; k-- {
p := q[0]
i, j := p[0], p[1]
q = q[1:]
if i == n-1 && j == n-1 {
return ans
}
for x := i - 1; x <= i+1; x++ {
for y := j - 1; y <= j+1; y++ {
if x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0 {
grid[x][y] = 1
q = append(q, [2]int{x, y})
}
}
}
}
}
return -1
}function shortestPathBinaryMatrix(grid: number[][]): number {
if (grid[0][0]) {
return -1;
}
const n = grid.length;
grid[0][0] = 1;
let q: number[][] = [[0, 0]];
for (let ans = 1; q.length > 0; ++ans) {
const nq: number[][] = [];
for (const [i, j] of q) {
if (i === n - 1 && j === n - 1) {
return ans;
}
for (let x = i - 1; x <= i + 1; ++x) {
for (let y = j - 1; y <= j + 1; ++y) {
if (x >= 0 && x < n && y >= 0 && y < n && !grid[x][y]) {
grid[x][y] = 1;
nq.push([x, y]);
}
}
}
}
q = nq;
}
return -1;
}use std::collections::VecDeque;
impl Solution {
pub fn shortest_path_binary_matrix(mut grid: Vec<Vec<i32>>) -> i32 {
let n = grid.len();
let mut queue = VecDeque::new();
queue.push_back([0, 0]);
let mut res = 0;
while !queue.is_empty() {
res += 1;
for _ in 0..queue.len() {
let [i, j] = queue.pop_front().unwrap();
if grid[i][j] == 1 {
continue;
}
if i == n - 1 && j == n - 1 {
return res;
}
grid[i][j] = 1;
for x in -1..=1 {
for y in -1..=1 {
let x = x + (i as i32);
let y = y + (j as i32);
if x < 0 || x == (n as i32) || y < 0 || y == (n as i32) {
continue;
}
queue.push_back([x as usize, y as usize]);
}
}
}
}
-1
}
}