README_EN.md

1217. Minimum Cost to Move Chips to The Same Position

中文文档

Description

We have n chips, where the position of the ith chip is position[i].

We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:

• position[i] + 2 or position[i] - 2 with cost = 0.
• position[i] + 1 or position[i] - 1 with cost = 1.

Return the minimum cost needed to move all the chips to the same position.

 

Example 1:

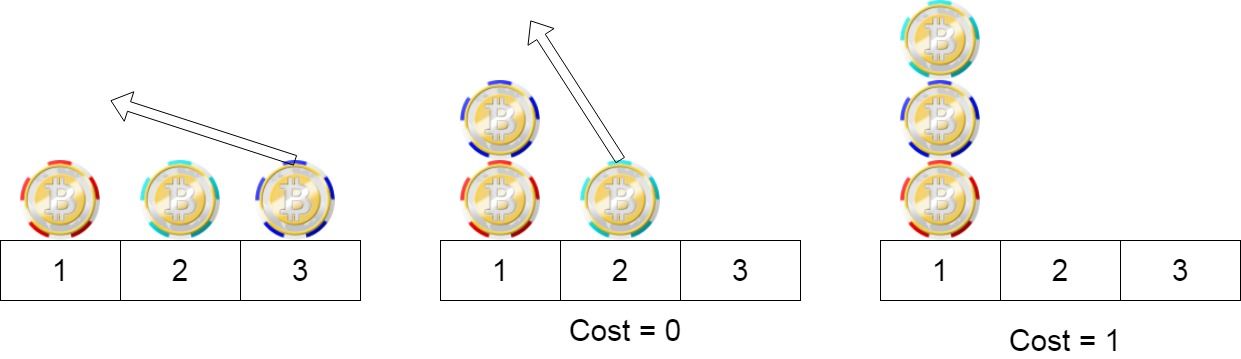
Input: position = [1,2,3]
Output: 1
Explanation: First step: Move the chip at position 3 to position 1 with cost = 0.
Second step: Move the chip at position 2 to position 1 with cost = 1.
Total cost is 1.

Example 2:

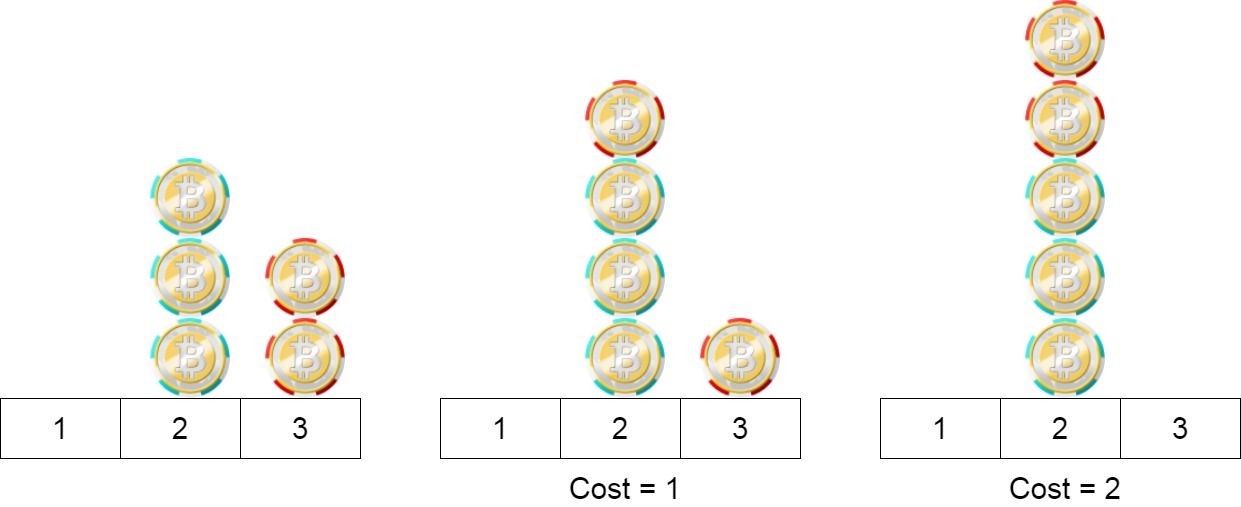
Input: position = [2,2,2,3,3]
Output: 2
Explanation: We can move the two chips at position  3 to position 2. Each move has cost = 1. The total cost = 2.

Example 3:

Input: position = [1,1000000000]
Output: 1

 

Constraints:

• 1 <= position.length <= 100
• 1 <= position[i] <= 10^9

Solutions

Solution 1: Quick Thinking

Move all chips at even indices to position 0, and all chips at odd indices to position 1, all at a cost of 0. Then, choose the position (either 0 or 1) with fewer chips and move these chips to the other position. The minimum cost required is the smaller quantity of chips.

The time complexity is $O(n)$, and the space complexity is $O(1)$. Here, $n$ is the number of chips.

class Solution:
    def minCostToMoveChips(self, position: List[int]) -> int:
        a = sum(p % 2 for p in position)
        b = len(position) - a
        return min(a, b)

class Solution {
    public int minCostToMoveChips(int[] position) {
        int a = 0;
        for (int p : position) {
            a += p % 2;
        }
        int b = position.length - a;
        return Math.min(a, b);
    }
}

class Solution {
public:
    int minCostToMoveChips(vector<int>& position) {
        int a = 0;
        for (auto& p : position) a += p & 1;
        int b = position.size() - a;
        return min(a, b);
    }
};

func minCostToMoveChips(position []int) int {
	a := 0
	for _, p := range position {
		a += p & 1
	}
	b := len(position) - a
	if a < b {
		return a
	}
	return b
}

/**
 * @param {number[]} position
 * @return {number}
 */
var minCostToMoveChips = function (position) {
    let a = 0;
    for (let v of position) {
        a += v % 2;
    }
    let b = position.length - a;
    return Math.min(a, b);
};