README.md

1232. 缀点成线

English Version

题目描述

给定一个数组 coordinates ，其中 coordinates[i] = [x, y] ， [x, y] 表示横坐标为 x、纵坐标为 y 的点。请你来判断，这些点是否在该坐标系中属于同一条直线上。

 

示例 1：

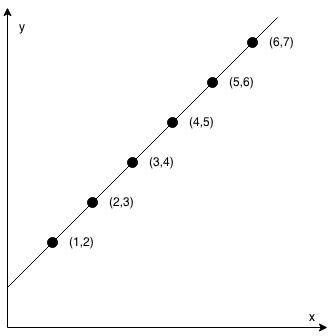
输入：coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
输出：true

示例 2：

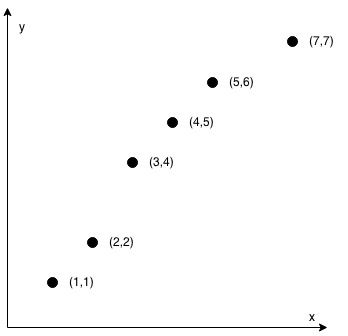
输入：coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
输出：false

 

提示：

• 2 <= coordinates.length <= 1000
• coordinates[i].length == 2
• -10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4
• coordinates 中不含重复的点

解法

方法一：数学

时间复杂度 $O(n)$，其中 $n$ 表示 coordinates 数组的长度。空间复杂度 $O(1)$。

class Solution:
    def checkStraightLine(self, coordinates: List[List[int]]) -> bool:
        x1, y1 = coordinates[0]
        x2, y2 = coordinates[1]
        for x, y in coordinates[2:]:
            if (x - x1) * (y2 - y1) != (y - y1) * (x2 - x1):
                return False
        return True

class Solution {
    public boolean checkStraightLine(int[][] coordinates) {
        int x1 = coordinates[0][0], y1 = coordinates[0][1];
        int x2 = coordinates[1][0], y2 = coordinates[1][1];
        for (int i = 2; i < coordinates.length; ++i) {
            int x = coordinates[i][0], y = coordinates[i][1];
            if ((x - x1) * (y2 - y1) != (y - y1) * (x2 - x1)) {
                return false;
            }
        }
        return true;
    }
}

class Solution {
public:
    bool checkStraightLine(vector<vector<int>>& coordinates) {
        int x1 = coordinates[0][0], y1 = coordinates[0][1];
        int x2 = coordinates[1][0], y2 = coordinates[1][1];
        for (int i = 2; i < coordinates.size(); ++i) {
            int x = coordinates[i][0], y = coordinates[i][1];
            if ((x - x1) * (y2 - y1) != (y - y1) * (x2 - x1)) {
                return false;
            }
        }
        return true;
    }
};

func checkStraightLine(coordinates [][]int) bool {
	x1, y1 := coordinates[0][0], coordinates[0][1]
	x2, y2 := coordinates[1][0], coordinates[1][1]
	for i := 2; i < len(coordinates); i++ {
		x, y := coordinates[i][0], coordinates[i][1]
		if (x-x1)*(y2-y1) != (y-y1)*(x2-x1) {
			return false
		}
	}
	return true
}