Skip to content

Latest commit

 

History

History
291 lines (250 loc) · 9.57 KB

README.md

File metadata and controls

291 lines (250 loc) · 9.57 KB
Raw

1349. 参加考试的最大学生数

English Version

题目描述

给你一个 m * n 的矩阵 seats 表示教室中的座位分布。如果座位是坏的（不可用），就用 '#' 表示；否则，用 '.' 表示。

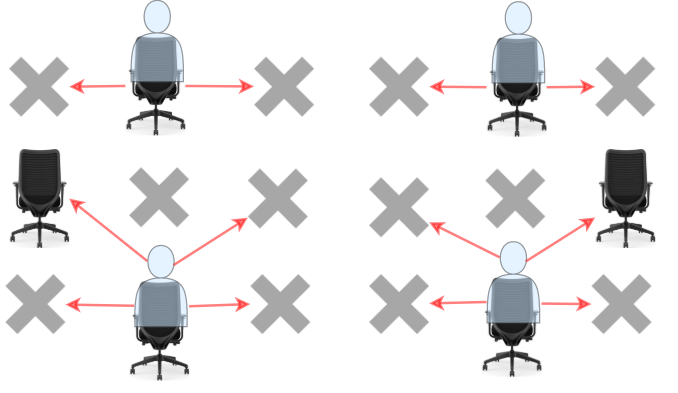
学生可以看到左侧、右侧、左上、右上这四个方向上紧邻他的学生的答卷，但是看不到直接坐在他前面或者后面的学生的答卷。请你计算并返回该考场可以容纳的同时参加考试且无法作弊的 最大 学生人数。

学生必须坐在状况良好的座位上。

 

示例 1：

输入：seats = [["#",".","#","#",".","#"],
              [".","#","#","#","#","."],
              ["#",".","#","#",".","#"]]
输出：4
解释：教师可以让 4 个学生坐在可用的座位上，这样他们就无法在考试中作弊。

示例 2：

输入：seats = [[".","#"],
              ["#","#"],
              ["#","."],
              ["#","#"],
              [".","#"]]
输出：3
解释：让所有学生坐在可用的座位上。

示例 3：

输入：seats = [["#",".",".",".","#"],
              [".","#",".","#","."],
              [".",".","#",".","."],
              [".","#",".","#","."],
              ["#",".",".",".","#"]]
输出：10
解释：让学生坐在第 1、3 和 5 列的可用座位上。

 

提示：

  • seats 只包含字符 '.' 和'#'
  • m == seats.length
  • n == seats[i].length
  • 1 <= m <= 8
  • 1 <= n <= 8

解法

方法一：状态压缩 + 记忆化搜索

我们注意到，每个座位有两种状态：可选和不可选。因此，我们可以使用二进制数来表示每一行的座位状态，其中 $1$ 表示可选，而 $0$ 表示不可选。例如，对于示例 $1$ 中的第一行，我们可以表示为 $010010$。因此，我们将初始座位转换为一个一维数组 $ss$，其中 $ss[i]$ 表示第 $i$ 行的座位状态。

接下来，我们设计一个函数 $dfs(seat, i)$，表示从第 $i$ 行开始，当前行的座位状态为 $seat$，可以容纳的最多学生人数。

我们可以枚举第 $i$ 行的所有选座状态 $mask$，并且判断 $mask$ 是否满足以下条件：

  • 状态 $mask$ 不能选择 $seat$ 之外的座位；
  • 状态 $mask$ 不能选择相邻的座位。

如果满足条件，我们求出当前行选择的座位个数 $cnt$，如果当前是最后一行，则更新函数的返回值，即 $ans = \max(ans, cnt)$。否则，我们继续递归地求解下一行的最大人数，下一行的座位状态 $nxt = ss[i + 1]$，并且需要排除当前行已选座位的左右两侧。然后我们递归地求解下一行的最大人数，即 $ans = \max(ans, cnt + dfs(nxt, i + 1))$。

最后，我们将 $ans$ 作为函数的返回值返回。

为了避免重复计算，我们可以使用记忆化搜索，将函数 $dfs(seat, i)$ 的返回值保存在一个二维数组 $f$ 中，其中 $f[seat][i]$ 表示从第 $i$ 行开始，当前行的座位状态为 $seat$，可以容纳的最多学生人数。

时间复杂度 $O(4^n \times n \times m)$，空间复杂度 $O(2^n \times m)$。其中 $m$ 和 $n$ 分别为座位的行数和列数。

class Solution:
    def maxStudents(self, seats: List[List[str]]) -> int:
        def f(seat: List[str]) -> int:
            mask = 0
            for i, c in enumerate(seat):
                if c == '.':
                    mask |= 1 << i
            return mask

        @cache
        def dfs(seat: int, i: int) -> int:
            ans = 0
            for mask in range(1 << n):
                if (seat | mask) != seat or (mask & (mask << 1)):
                    continue
                cnt = mask.bit_count()
                if i == len(ss) - 1:
                    ans = max(ans, cnt)
                else:
                    nxt = ss[i + 1]
                    nxt &= ~(mask << 1)
                    nxt &= ~(mask >> 1)
                    ans = max(ans, cnt + dfs(nxt, i + 1))
            return ans

        n = len(seats[0])
        ss = [f(s) for s in seats]
        return dfs(ss[0], 0)
class Solution {
    private Integer[][] f;
    private int n;
    private int[] ss;

    public int maxStudents(char[][] seats) {
        int m = seats.length;
        n = seats[0].length;
        ss = new int[m];
        f = new Integer[1 << n][m];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (seats[i][j] == '.') {
                    ss[i] |= 1 << j;
                }
            }
        }
        return dfs(ss[0], 0);
    }

    private int dfs(int seat, int i) {
        if (f[seat][i] != null) {
            return f[seat][i];
        }
        int ans = 0;
        for (int mask = 0; mask < 1 << n; ++mask) {
            if ((seat | mask) != seat || (mask & (mask << 1)) != 0) {
                continue;
            }
            int cnt = Integer.bitCount(mask);
            if (i == ss.length - 1) {
                ans = Math.max(ans, cnt);
            } else {
                int nxt = ss[i + 1];
                nxt &= ~(mask << 1);
                nxt &= ~(mask >> 1);
                ans = Math.max(ans, cnt + dfs(nxt, i + 1));
            }
        }
        return f[seat][i] = ans;
    }
}
class Solution {
public:
    int maxStudents(vector<vector<char>>& seats) {
        int m = seats.size();
        int n = seats[0].size();
        vector<int> ss(m);
        vector<vector<int>> f(1 << n, vector<int>(m, -1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (seats[i][j] == '.') {
                    ss[i] |= 1 << j;
                }
            }
        }
        function<int(int, int)> dfs = [&](int seat, int i) -> int {
            if (f[seat][i] != -1) {
                return f[seat][i];
            }
            int ans = 0;
            for (int mask = 0; mask < 1 << n; ++mask) {
                if ((seat | mask) != seat || (mask & (mask << 1)) != 0) {
                    continue;
                }
                int cnt = __builtin_popcount(mask);
                if (i == m - 1) {
                    ans = max(ans, cnt);
                } else {
                    int nxt = ss[i + 1];
                    nxt &= ~(mask >> 1);
                    nxt &= ~(mask << 1);
                    ans = max(ans, cnt + dfs(nxt, i + 1));
                }
            }
            return f[seat][i] = ans;
        };
        return dfs(ss[0], 0);
    }
};
func maxStudents(seats [][]byte) int {
	m, n := len(seats), len(seats[0])
	ss := make([]int, m)
	f := make([][]int, 1<<n)
	for i, seat := range seats {
		for j, c := range seat {
			if c == '.' {
				ss[i] |= 1 << j
			}
		}
	}
	for i := range f {
		f[i] = make([]int, m)
		for j := range f[i] {
			f[i][j] = -1
		}
	}
	var dfs func(int, int) int
	dfs = func(seat, i int) int {
		if f[seat][i] != -1 {
			return f[seat][i]
		}
		ans := 0
		for mask := 0; mask < 1<<n; mask++ {
			if (seat|mask) != seat || (mask&(mask<<1)) != 0 {
				continue
			}
			cnt := bits.OnesCount(uint(mask))
			if i == m-1 {
				ans = max(ans, cnt)
			} else {
				nxt := ss[i+1] & ^(mask >> 1) & ^(mask << 1)
				ans = max(ans, cnt+dfs(nxt, i+1))
			}
		}
		f[seat][i] = ans
		return ans
	}
	return dfs(ss[0], 0)
}
function maxStudents(seats: string[][]): number {
    const m: number = seats.length;
    const n: number = seats[0].length;
    const ss: number[] = Array(m).fill(0);
    const f: number[][] = Array.from({ length: 1 << n }, () => Array(m).fill(-1));
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (seats[i][j] === '.') {
                ss[i] |= 1 << j;
            }
        }
    }

    const dfs = (seat: number, i: number): number => {
        if (f[seat][i] !== -1) {
            return f[seat][i];
        }
        let ans: number = 0;
        for (let mask = 0; mask < 1 << n; ++mask) {
            if ((seat | mask) !== seat || (mask & (mask << 1)) !== 0) {
                continue;
            }
            const cnt: number = mask.toString(2).split('1').length - 1;
            if (i === m - 1) {
                ans = Math.max(ans, cnt);
            } else {
                let nxt: number = ss[i + 1];
                nxt &= ~(mask >> 1);
                nxt &= ~(mask << 1);
                ans = Math.max(ans, cnt + dfs(nxt, i + 1));
            }
        }
        return (f[seat][i] = ans);
    };
    return dfs(ss[0], 0);
}