给定一个算术表达式的后缀表示法的标记(token) postfix ,构造并返回该表达式对应的二叉表达式树。
后缀表示法是一种将操作数写在运算符之前的表示法。例如,表达式 4*(5-(2+7)) 的后缀表示法表示为数组 postfix = ["4","5","7","2","+","-","*"] 。
抽象类 Node 需要用于实现二叉表达式树。我们将通过 evaluate 函数来测试返回的树是否能够解析树中的值。你不可以移除 Node 类,但你可以按需修改此类,也可以定义其他类来实现它。
二叉表达式树是一种表达算术表达式的二叉树。二叉表达式树中的每一个节点都有零个或两个子节点。 叶节点(有 0 个子节点的节点)表示操作数,非叶节点(有 2 个子节点的节点)表示运算符: '+' (加)、 '-' (减)、 '*' (乘)和 '/' (除)。
我们保证任何子树对应值的绝对值不超过 109 ,且所有操作都是有效的(即没有除以零的操作)
进阶: 你可以将表达式树设计得更模块化吗?例如,你的设计能够不修改现有的 evaluate 的实现就能支持更多的操作符吗?
示例 1:
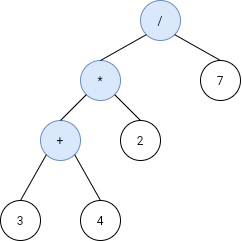
输入: s = ["3","4","+","2","*","7","/"]
输出: 2
解释: 此表达式可解析为上述二叉树,其对应表达式为 ((3+4)*2)/7) = 14/7 = 2.
示例 2:
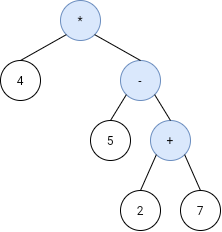
输入: s = ["4","5","7","2","+","-","*"]
输出: -16
解释: 此表达式可解析为上述二叉树,其对应表达式为 4*(5-(2+7)) = 4*(-4) = -16.
提示:
1 <= s.length < 100s.length是奇数。s包含数字和字符'+'、'-'、'*'以及'/'。- 如果
s[i]是数,则对应的整数不超过105。 s保证是一个有效的表达式。- 结果值和所有过程值的绝对值均不超过
109。 - 保证表达式不包含除以零的操作。
import abc
from abc import ABC, abstractmethod
"""
This is the interface for the expression tree Node.
You should not remove it, and you can define some classes to implement it.
"""
class Node(ABC):
@abstractmethod
# define your fields here
def evaluate(self) -> int:
pass
class MyNode(Node):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
def evaluate(self) -> int:
x = self.val
if x.isdigit():
return int(x)
left, right = self.left.evaluate(), self.right.evaluate()
if x == '+':
return left + right
if x == '-':
return left - right
if x == '*':
return left * right
if x == '/':
return left // right
"""
This is the TreeBuilder class.
You can treat it as the driver code that takes the postinfix input
and returns the expression tree represnting it as a Node.
"""
class TreeBuilder(object):
def buildTree(self, postfix: List[str]) -> 'Node':
stk = []
for s in postfix:
node = MyNode(s)
if not s.isdigit():
node.right = stk.pop()
node.left = stk.pop()
stk.append(node)
return stk[-1]
"""
Your TreeBuilder object will be instantiated and called as such:
obj = TreeBuilder();
expTree = obj.buildTree(postfix);
ans = expTree.evaluate();
"""/**
* This is the interface for the expression tree Node.
* You should not remove it, and you can define some classes to implement it.
*/
abstract class Node {
public abstract int evaluate();
// define your fields here
protected String val;
protected Node left;
protected Node right;
};
class MyNode extends Node {
public MyNode(String val) {
this.val = val;
}
public int evaluate() {
if (isNumeric()) {
return Integer.parseInt(val);
}
int leftVal = left.evaluate();
int rightVal = right.evaluate();
if (Objects.equals(val, "+")) {
return leftVal + rightVal;
}
if (Objects.equals(val, "-")) {
return leftVal - rightVal;
}
if (Objects.equals(val, "*")) {
return leftVal * rightVal;
}
if (Objects.equals(val, "/")) {
return leftVal / rightVal;
}
return 0;
}
public boolean isNumeric() {
for (char c : val.toCharArray()) {
if (!Character.isDigit(c)) {
return false;
}
}
return true;
}
}
/**
* This is the TreeBuilder class.
* You can treat it as the driver code that takes the postinfix input
* and returns the expression tree represnting it as a Node.
*/
class TreeBuilder {
Node buildTree(String[] postfix) {
Deque<MyNode> stk = new ArrayDeque<>();
for (String s : postfix) {
MyNode node = new MyNode(s);
if (!node.isNumeric()) {
node.right = stk.pop();
node.left = stk.pop();
}
stk.push(node);
}
return stk.peek();
}
};
/**
* Your TreeBuilder object will be instantiated and called as such:
* TreeBuilder obj = new TreeBuilder();
* Node expTree = obj.buildTree(postfix);
* int ans = expTree.evaluate();
*//**
* This is the interface for the expression tree Node.
* You should not remove it, and you can define some classes to implement it.
*/
class Node {
public:
virtual ~Node(){};
virtual int evaluate() const = 0;
protected:
// define your fields here
string val;
Node* left;
Node* right;
};
class MyNode : public Node {
public:
MyNode(string val) {
this->val = val;
}
MyNode(string val, Node* left, Node* right) {
this->val = val;
this->left = left;
this->right = right;
}
int evaluate() const {
if (!(val == "+" || val == "-" || val == "*" || val == "/")) return stoi(val);
auto leftVal = left->evaluate(), rightVal = right->evaluate();
if (val == "+") return leftVal + rightVal;
if (val == "-") return leftVal - rightVal;
if (val == "*") return leftVal * rightVal;
if (val == "/") return leftVal / rightVal;
return 0;
}
};
/**
* This is the TreeBuilder class.
* You can treat it as the driver code that takes the postinfix input
* and returns the expression tree represnting it as a Node.
*/
class TreeBuilder {
public:
Node* buildTree(vector<string>& postfix) {
stack<MyNode*> stk;
for (auto s : postfix) {
MyNode* node;
if (s == "+" || s == "-" || s == "*" || s == "/") {
auto right = stk.top();
stk.pop();
auto left = stk.top();
stk.pop();
node = new MyNode(s, left, right);
} else {
node = new MyNode(s);
}
stk.push(node);
}
return stk.top();
}
};
/**
* Your TreeBuilder object will be instantiated and called as such:
* TreeBuilder* obj = new TreeBuilder();
* Node* expTree = obj->buildTree(postfix);
* int ans = expTree->evaluate();
*/