Given n cuboids where the dimensions of the ith cuboid is cuboids[i] = [widthi, lengthi, heighti] (0-indexed). Choose a subset of cuboids and place them on each other.
You can place cuboid i on cuboid j if widthi <= widthj and lengthi <= lengthj and heighti <= heightj. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.
Return the maximum height of the stacked cuboids.
Example 1:
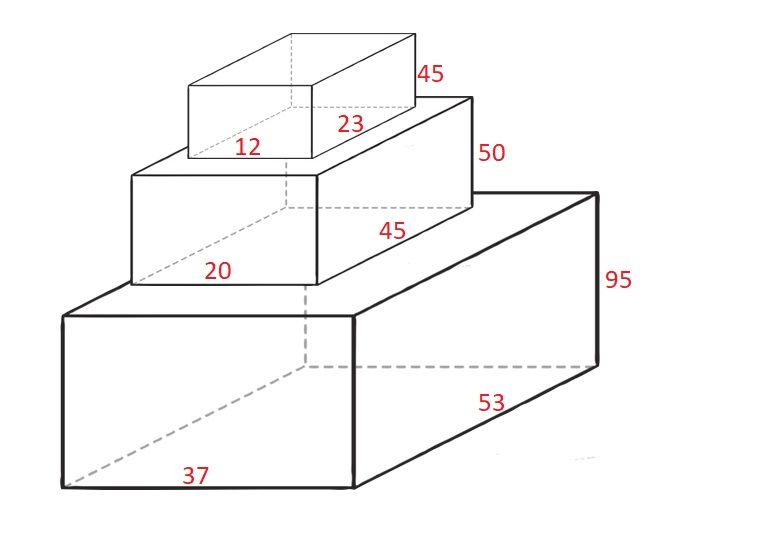
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]] Output: 190 Explanation: Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95. Cuboid 0 is placed next with the 45x20 side facing down with height 50. Cuboid 2 is placed next with the 23x12 side facing down with height 45. The total height is 95 + 50 + 45 = 190.
Example 2:
Input: cuboids = [[38,25,45],[76,35,3]] Output: 76 Explanation: You can't place any of the cuboids on the other. We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.
Example 3:
Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]] Output: 102 Explanation: After rearranging the cuboids, you can see that all cuboids have the same dimension. You can place the 11x7 side down on all cuboids so their heights are 17. The maximum height of stacked cuboids is 6 * 17 = 102.
Constraints:
n == cuboids.length1 <= n <= 1001 <= widthi, lengthi, heighti <= 100
According to the problem description, box
This problem allows us to rotate the boxes, which means we can choose any side of the box as the "height". For any legal stacking, if we rotate each box in it to "length <= width <= height", the stacking is still legal and can ensure the maximum height of the stacking.
Therefore, we can sort all the sides of the boxes so that each box satisfies "length <= width <= height". Then we sort each box in ascending order.
Next, we can use dynamic programming to solve this problem.
We define
where
The final answer is the maximum value of
The time complexity is
class Solution:
def maxHeight(self, cuboids: List[List[int]]) -> int:
for c in cuboids:
c.sort()
cuboids.sort()
n = len(cuboids)
f = [0] * n
for i in range(n):
for j in range(i):
if cuboids[j][1] <= cuboids[i][1] and cuboids[j][2] <= cuboids[i][2]:
f[i] = max(f[i], f[j])
f[i] += cuboids[i][2]
return max(f)class Solution {
public int maxHeight(int[][] cuboids) {
for (var c : cuboids) {
Arrays.sort(c);
}
Arrays.sort(cuboids,
(a, b) -> a[0] == b[0] ? (a[1] == b[1] ? a[2] - b[2] : a[1] - b[1]) : a[0] - b[0]);
int n = cuboids.length;
int[] f = new int[n];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
if (cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]) {
f[i] = Math.max(f[i], f[j]);
}
}
f[i] += cuboids[i][2];
}
return Arrays.stream(f).max().getAsInt();
}
}class Solution {
public:
int maxHeight(vector<vector<int>>& cuboids) {
for (auto& c : cuboids) {
sort(c.begin(), c.end());
}
sort(cuboids.begin(), cuboids.end());
int n = cuboids.size();
vector<int> f(n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
if (cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]) {
f[i] = max(f[i], f[j]);
}
}
f[i] += cuboids[i][2];
}
return *max_element(f.begin(), f.end());
}
};func maxHeight(cuboids [][]int) int {
for _, c := range cuboids {
sort.Ints(c)
}
sort.Slice(cuboids, func(i, j int) bool {
a, b := cuboids[i], cuboids[j]
return a[0] < b[0] || a[0] == b[0] && (a[1] < b[1] || a[1] == b[1] && a[2] < b[2])
})
n := len(cuboids)
f := make([]int, n)
for i := range f {
for j := 0; j < i; j++ {
if cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2] {
f[i] = max(f[i], f[j])
}
}
f[i] += cuboids[i][2]
}
return slices.Max(f)
}function maxHeight(cuboids: number[][]): number {
for (const c of cuboids) {
c.sort((a, b) => a - b);
}
cuboids.sort((a, b) => {
if (a[0] !== b[0]) {
return a[0] - b[0];
}
if (a[1] !== b[1]) {
return a[1] - b[1];
}
return a[2] - b[2];
});
const n = cuboids.length;
const f = Array(n).fill(0);
for (let i = 0; i < n; ++i) {
for (let j = 0; j < i; ++j) {
const ok = cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2];
if (ok) f[i] = Math.max(f[i], f[j]);
}
f[i] += cuboids[i][2];
}
return Math.max(...f);
}/**
* @param {number[][]} cuboids
* @return {number}
*/
var maxHeight = function (cuboids) {
for (const c of cuboids) {
c.sort((a, b) => a - b);
}
cuboids.sort((a, b) => {
if (a[0] !== b[0]) {
return a[0] - b[0];
}
if (a[1] !== b[1]) {
return a[1] - b[1];
}
return a[2] - b[2];
});
const n = cuboids.length;
const f = Array(n).fill(0);
for (let i = 0; i < n; ++i) {
for (let j = 0; j < i; ++j) {
const ok = cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2];
if (ok) f[i] = Math.max(f[i], f[j]);
}
f[i] += cuboids[i][2];
}
return Math.max(...f);
};