给你一个炸弹列表。一个炸弹的 爆炸范围 定义为以炸弹为圆心的一个圆。
炸弹用一个下标从 0 开始的二维整数数组 bombs 表示,其中 bombs[i] = [xi, yi, ri] 。xi 和 yi 表示第 i 个炸弹的 X 和 Y 坐标,ri 表示爆炸范围的 半径 。
你需要选择引爆 一个 炸弹。当这个炸弹被引爆时,所有 在它爆炸范围内的炸弹都会被引爆,这些炸弹会进一步将它们爆炸范围内的其他炸弹引爆。
给你数组 bombs ,请你返回在引爆 一个 炸弹的前提下,最多 能引爆的炸弹数目。
示例 1:
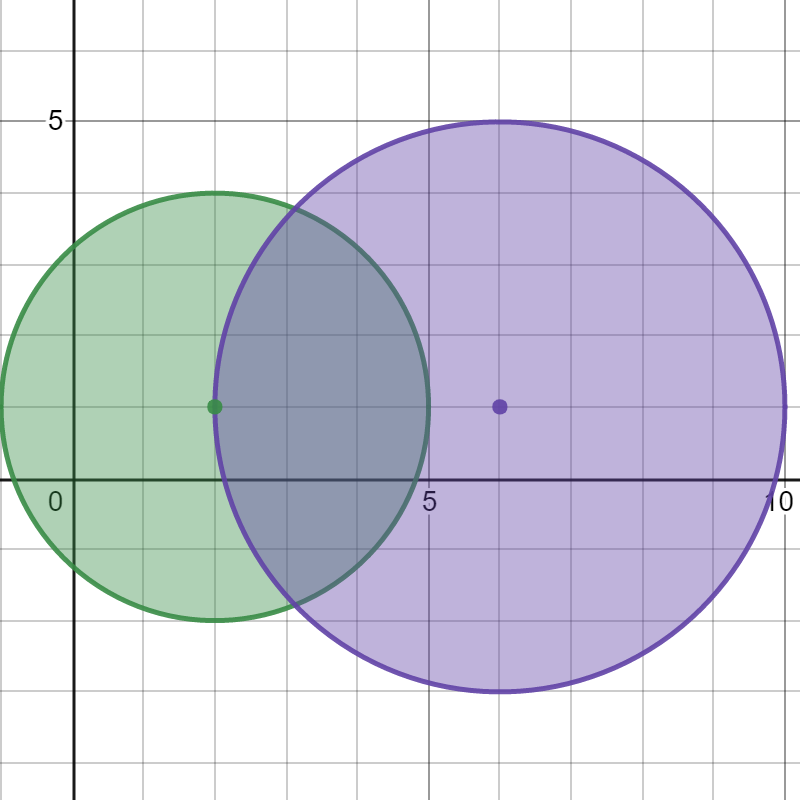
输入:bombs = [[2,1,3],[6,1,4]] 输出:2 解释: 上图展示了 2 个炸弹的位置和爆炸范围。 如果我们引爆左边的炸弹,右边的炸弹不会被影响。 但如果我们引爆右边的炸弹,两个炸弹都会爆炸。 所以最多能引爆的炸弹数目是 max(1, 2) = 2 。
示例 2:
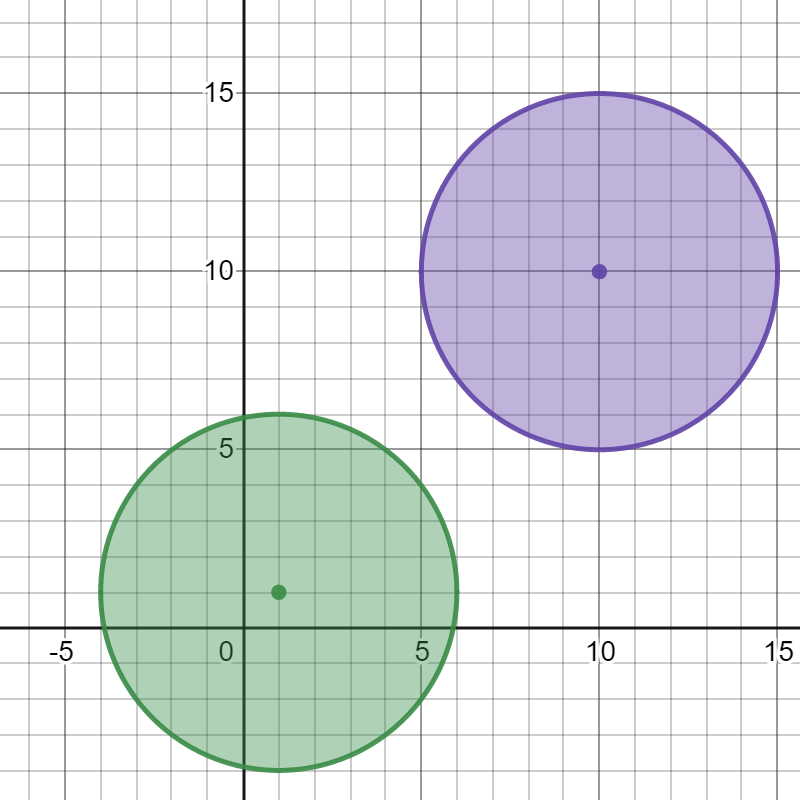
输入:bombs = [[1,1,5],[10,10,5]] 输出:1 解释: 引爆任意一个炸弹都不会引爆另一个炸弹。所以最多能引爆的炸弹数目为 1 。
示例 3:
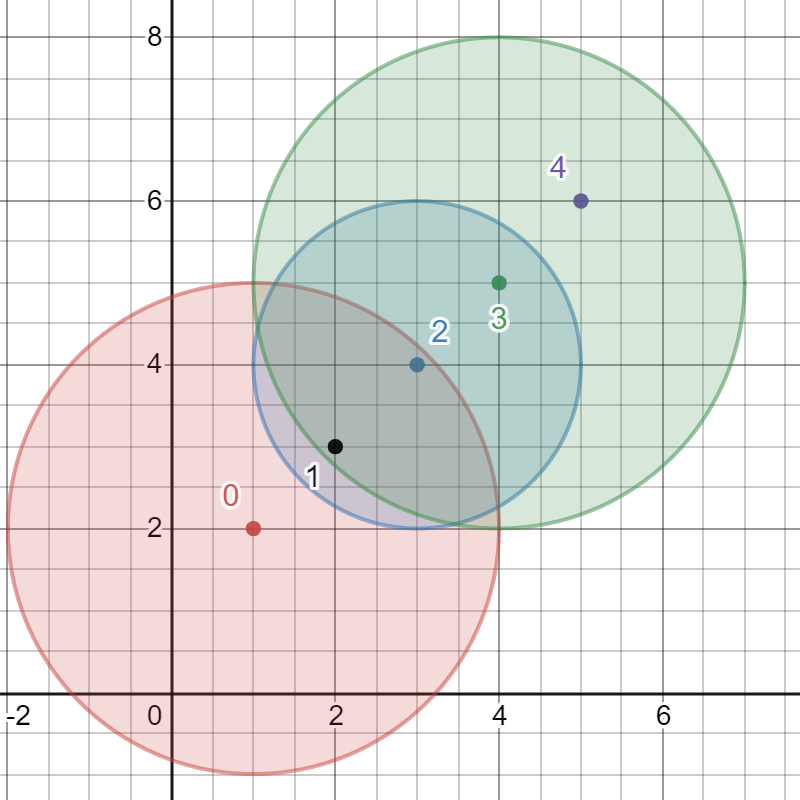
输入:bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]] 输出:5 解释: 最佳引爆炸弹为炸弹 0 ,因为: - 炸弹 0 引爆炸弹 1 和 2 。红色圆表示炸弹 0 的爆炸范围。 - 炸弹 2 引爆炸弹 3 。蓝色圆表示炸弹 2 的爆炸范围。 - 炸弹 3 引爆炸弹 4 。绿色圆表示炸弹 3 的爆炸范围。 所以总共有 5 个炸弹被引爆。
提示:
1 <= bombs.length <= 100bombs[i].length == 31 <= xi, yi, ri <= 105
枚举每个炸弹 k 作为起始引爆点,BFS 搜索能影响到的所有炸弹的数量,取其最大值。
class Solution:
def maximumDetonation(self, bombs: List[List[int]]) -> int:
def check(i, j):
if i == j:
return False
x, y = bombs[i][0] - bombs[j][0], bombs[i][1] - bombs[j][1]
r = bombs[i][2]
return r * r >= x * x + y * y
g = defaultdict(list)
n = len(bombs)
for i in range(n):
for j in range(n):
if check(i, j):
g[i].append(j)
ans = 0
for k in range(n):
q = deque([k])
vis = [False] * n
vis[k] = True
cnt = 0
while q:
i = q.popleft()
cnt += 1
for j in g[i]:
if not vis[j]:
vis[j] = True
q.append(j)
ans = max(ans, cnt)
return ansclass Solution {
private int[][] bombs;
public int maximumDetonation(int[][] bombs) {
this.bombs = bombs;
int n = bombs.length;
boolean[][] g = new boolean[n][n];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
g[i][j] = check(i, j);
}
}
int ans = 0;
for (int k = 0; k < n; ++k) {
Deque<Integer> q = new ArrayDeque<>();
q.offer(k);
boolean[] vis = new boolean[n];
vis[k] = true;
int cnt = 0;
while (!q.isEmpty()) {
int i = q.poll();
++cnt;
for (int j = 0; j < n; ++j) {
if (g[i][j] && !vis[j]) {
vis[j] = true;
q.offer(j);
}
}
}
ans = Math.max(ans, cnt);
}
return ans;
}
private boolean check(int i, int j) {
if (i == j) {
return false;
}
long x = bombs[i][0] - bombs[j][0];
long y = bombs[i][1] - bombs[j][1];
long r = bombs[i][2];
return r * r >= x * x + y * y;
}
}class Solution {
public:
int maximumDetonation(vector<vector<int>>& bombs) {
int n = bombs.size();
vector<vector<bool>> g(n, vector<bool>(n));
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
g[i][j] = check(i, j, bombs);
int ans = 0;
for (int k = 0; k < n; ++k) {
queue<int> q{{k}};
vector<bool> vis(n);
vis[k] = true;
int cnt = 0;
while (!q.empty()) {
int i = q.front();
q.pop();
++cnt;
for (int j = 0; j < n; ++j) {
if (g[i][j] && !vis[j]) {
vis[j] = true;
q.push(j);
}
}
}
ans = max(ans, cnt);
}
return ans;
}
bool check(int i, int j, vector<vector<int>>& bombs) {
if (i == j) return false;
long long x = bombs[i][0] - bombs[j][0];
long long y = bombs[i][1] - bombs[j][1];
long long r = bombs[i][2];
return r * r >= x * x + y * y;
}
};func maximumDetonation(bombs [][]int) int {
check := func(i, j int) bool {
if i == j {
return false
}
x, y := bombs[i][0]-bombs[j][0], bombs[i][1]-bombs[j][1]
r := bombs[i][2]
return r*r >= x*x+y*y
}
n := len(bombs)
g := make([][]bool, n)
for i := range g {
g[i] = make([]bool, n)
for j := range g[i] {
g[i][j] = check(i, j)
}
}
ans := 0
for k := 0; k < n; k++ {
q := []int{k}
vis := make([]bool, n)
vis[k] = true
cnt := 0
for len(q) > 0 {
i := q[0]
q = q[1:]
cnt++
for j := 0; j < n; j++ {
if g[i][j] && !vis[j] {
vis[j] = true
q = append(q, j)
}
}
}
ans = max(ans, cnt)
}
return ans
}