You are given an integer n and a 0-indexed 2D array queries where queries[i] = [typei, indexi, vali].
Initially, there is a 0-indexed n x n matrix filled with 0's. For each query, you must apply one of the following changes:
- if
typei == 0, set the values in the row withindexitovali, overwriting any previous values. - if
typei == 1, set the values in the column withindexitovali, overwriting any previous values.
Return the sum of integers in the matrix after all queries are applied.
Example 1:
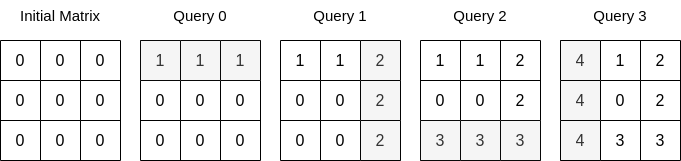
Input: n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]] Output: 23 Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 23.
Example 2:
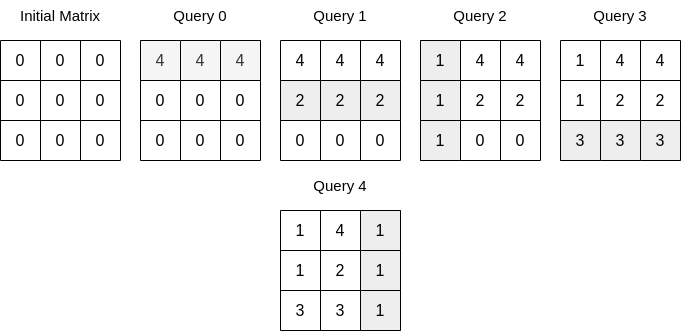
Input: n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]] Output: 17 Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 17.
Constraints:
1 <= n <= 1041 <= queries.length <= 5 * 104queries[i].length == 30 <= typei <= 10 <= indexi < n0 <= vali <= 105
Since the value of each row and column depends on the last modification, we can traverse all queries in reverse order and use hash tables
For each query
- If
$t = 0$ , we check whether the $i$th row has been modified. If not, we add$v \times (n - |col|)$ to the answer, where$|col|$ represents the size of$col$ , and then add$i$ to$row$ . - If
$t = 1$ , we check whether the $i$th column has been modified. If not, we add$v \times (n - |row|)$ to the answer, where$|row|$ represents the size of$row$ , and then add$i$ to$col$ .
Finally, return the answer.
The time complexity is
class Solution:
def matrixSumQueries(self, n: int, queries: List[List[int]]) -> int:
row = set()
col = set()
ans = 0
for t, i, v in queries[::-1]:
if t == 0:
if i not in row:
ans += v * (n - len(col))
row.add(i)
else:
if i not in col:
ans += v * (n - len(row))
col.add(i)
return ansclass Solution {
public long matrixSumQueries(int n, int[][] queries) {
Set<Integer> row = new HashSet<>();
Set<Integer> col = new HashSet<>();
int m = queries.length;
long ans = 0;
for (int k = m - 1; k >= 0; --k) {
var q = queries[k];
int t = q[0], i = q[1], v = q[2];
if (t == 0) {
if (row.add(i)) {
ans += 1L * (n - col.size()) * v;
}
} else {
if (col.add(i)) {
ans += 1L * (n - row.size()) * v;
}
}
}
return ans;
}
}class Solution {
public:
long long matrixSumQueries(int n, vector<vector<int>>& queries) {
unordered_set<int> row, col;
reverse(queries.begin(), queries.end());
long long ans = 0;
for (auto& q : queries) {
int t = q[0], i = q[1], v = q[2];
if (t == 0) {
if (!row.count(i)) {
ans += 1LL * (n - col.size()) * v;
row.insert(i);
}
} else {
if (!col.count(i)) {
ans += 1LL * (n - row.size()) * v;
col.insert(i);
}
}
}
return ans;
}
};func matrixSumQueries(n int, queries [][]int) (ans int64) {
row, col := map[int]bool{}, map[int]bool{}
m := len(queries)
for k := m - 1; k >= 0; k-- {
t, i, v := queries[k][0], queries[k][1], queries[k][2]
if t == 0 {
if !row[i] {
ans += int64(v * (n - len(col)))
row[i] = true
}
} else {
if !col[i] {
ans += int64(v * (n - len(row)))
col[i] = true
}
}
}
return
}function matrixSumQueries(n: number, queries: number[][]): number {
const row: Set<number> = new Set();
const col: Set<number> = new Set();
let ans = 0;
queries.reverse();
for (const [t, i, v] of queries) {
if (t === 0) {
if (!row.has(i)) {
ans += v * (n - col.size);
row.add(i);
}
} else {
if (!col.has(i)) {
ans += v * (n - row.size);
col.add(i);
}
}
}
return ans;
}