| layout | mathjax | permalink |
|---|---|---|
page |
true |
vizinhoMaisProximo/ |
Tabela de Conteúdos:
- Sobre o algoritmo do vizinho mais próximo
- Imagens digitais
- Um pouco mais sobre digitalização de imagens
- A proposta do algoritmo NN
- Hora de estudar código Java e testar
Dica: Após visitar um link da tabela de conteúdos, utilize a tecla de retorno do seu navegador para voltar para a tabela.
O algoritmo do vizinho mais próximo, chamado também de nn (nearest neighbourg, em inglês) vai ser o primeiro a ser apresentado. Vamos construir um programa destinado a classificar imagens. O nn não apresenta desempenho razoável para realizar classificação de imagens. Não quer dizer que seja inútil, na verdade, pode ter uso prático com bons resultados em outras atividades. A vantagem de começar por ele é que as operações que ele realiza nos dados das imagens são de baixa complexidade. Desta forma, o nn vai nos permitir introduzir código para obter os dados de imagens a partir de arquivos, e código capaz de operar nestas grandes quantidades de dados. É um primeiro passo para aprender a desenvolver algoritmos mais eficientes, como redes neurais e convolucionais. E, apesar do desempenho ser fraco, não é desprovido de significado. Ao executar o nn utilizando a base CIFAR-10, ele obtém um percentual de acerto em torno de 30%. Se os acertos fossem obra do acaso, como existem 10 categorias de imagens na base de dados, ficaria em torno de 10%.
Imagens são armazenadas em um computador como um conjunto de pixeis. Uma das maneiras mais simples de armazenar imagens digitais coloridas utiliza a forma RGB (vermelho, verde e azul, ou red, green e blue, do inglês). Cada pixel é um ponto da imagem, representando uma cor. Todas as cores são obtidas variando a intensidade de vermelho, verde e azul. Uma cor portanto é codificada através de três números inteiros, que variam de 0 a 255, e que determinam o peso de cada uma das três cores citadas.
Observe uma imagem, como a da Figura 1: Ao ser digitalizada, se transforma em uma fila de bytes, como a da Figura 2.
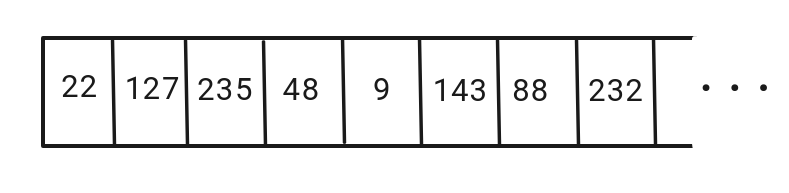
- Quando uma pessoa vê uma imagem, percebe cores, formas, identifica objetos.
- Quando um programa de computador vê uma imagem, tem diante de si uma sequência de números.
- Creio que podemos afirmar que pessoas e programas de computador vêm imagens de forma diferente. (Será mesmo? Se examinarmos o processo da visão humana ... Bom, vamos deixar como está por enquanto).
Mas, o que realmente importa, não é como cada um observa e processa a imagem, mas sim, se é possível que um programa de computador obtenha resultados equivalentes, ao observar e processar uma imagem, dos resultados obtidos por uma pessoa.
Construímos programas de aprendizagem de máquina considerando que a resposta a esta pergunta teórica é sim. Podemos considerar que, se obtivermos resultados equivalentes, a teoria está correta. Provavelmente o próprio Alan Turing concordaria com isso!
Como programas de computadores de aprendizagem de máquina têm sido bem sucedidos, ás vezes com resultados melhores do que as pessoas, em tarefas como classificar images, vamos entender isso como evidência de que, da mesma forma que pessoas percebem cores, formas, e identificam objetos em imagens, algo semelhante ocorre quando um programa de computador vê os números de uma imagem digital.
Comparabilidade é uma propriedade matemática que permite tomar decisões operando valores. Podemos aplicar lógica em dados se eles são comparáveis. Vamos esperar que, assim como uma pessoa vê semelhanças e diferenças ao comparar duas imagens diferentes, um programa de computador possa perceber as mesmas semelhanças e diferenças comparando os números digitalizados das mesmas duas imagens.
O que vai portanto determinar os algoritmos que vamos usar em aprendizagem de máquina são as operações matemáticas que vamos aplicar aos números, aos valores.
Mencionamos acima que se utilizam mais de uma maneira de codificar as cores das imagens. Além disto, utiliza-se mais de uma forma para codificar a posição dos pixeis de uma imagem digitalizada.
Uma ordem natural seria armazenar os pixeis da esquerda para direita, de cima para baixo. Mas outras são utilizadas.
As imagens da base de dados Cifar-10 que vamos utilizar aqui em nosso exemplo armazenam os pixeis em uma ordem um pouco diferente. Isso precisa ser considerado se vamos construir um algoritmo para reproduzir a imagem na tela de um computador. E vai ser, quando formos cuidar disto.
O que queremos estabelecer aqui é outra coisa. Ao aplicar operações matemáticas em dados de duas ou mais imagens diferentes não é necessário que os dados estejam na ordem natural, apenas é necessário que estejam em ordens iguais. Comutatividade (a+b = b+a), associatividade (a+(b+c) = ((a+b)+c), e outras propriedades de operações são úteis para explicar estas manobras com exatidão, mas explicá-las aquí foge ao escopo da obra.
Ao comparar duas imagens, o algoritmo nn pretende obter algo chamado de distancia entre elas. A distância vai ser a soma de todas as diferenças entre os pixeis nas mesmas posições das imagens.
Uma imagem de 32x32 pixeis na forma RGB, possui 32x32x3 bytes, totalizando 3072 bytes.
Suponha que temos imagens disponíveis em dois conjuntos de imagens distintos, um de teste (CTE) e outro de treino (CTR).
Vamos considerar duas imagens diferentes, retiradas de cada um destes conjuntos, $$ Te \ne Tr $$.
Vamos representar a sequência dos bytes de cada uma das imagens como (n = 3072):
A distância utilizada pelo nn vai ser:
Ou seja, vai ser a soma dos valores absolutos das diferenças de cada um dos bytes de
Vamos conjecturar sobre a base desta operação. Se, ao invés de
Faz sentido, a distancia entre duas imagens iguais é 0!
Vamos conjecturar sobre o crescimento indutivo da distância. Imagine que as imagens são praticamente iguais, que apenas o primeiro byte de
Faz sentido para duas imagens praticamente iguais!
Finalmente, vamos conjecturar porque somamos os valores absolutos das diferenças. Imaginemos que as duas imagens diferentes acima tivessem não apenas os bytes na primeira posição diferentes, mas os da segunda também. E que os bytes da segunda posição fossem
Mas isto não faz sentido, pois as imagens com apenas um byte diferente resultariam em uma distancia de
Porém, se somarmos as diferenças absolutas, no caso das imagens com os dois primeiros bytes diferentes, teríamos uma distancia
de
Agora sim, faz sentido: as imagens com os dois primeiros bytes diferentes resultam em uma distância =
Visite a área de código do projeto, estude as classes NearestNeighbourgh.java e Cifar10Utils.java.
Recomenda-se fortemente começar lendo e estudando a classe Cifar10Utils.java, para em seguida estudar a classe NearestNeighbourgh.java. Ambas estão bem comentadas e trazem explicações importantes tanto no aspecto dos dados a serem utilizados, bem como com relação ao algoritmo e também possuem explicações relativas ao código Java. Os comentários estão escritos tanto em inglês como em português. Se deseja ler em português, basta ir avançando que ao final do texto em inglês encontra-se uma linha, Portuguese version:, a partir da qual o comentário é repetido em português.
Em seguida, sugerimos retornar à pagina inicial, e estudar a lição de como clonar o projeto utilizando o NetBeans IDE./duodecimoMachineLearning/wiki/clonarProjetoNetbeansIDE) para rodar o código.
Eis um exemplo de resultado obtido ao rodar o NearestNeighbourgh utilizando 100% dos dados do CIFAR-10:
Accuracy = 38.59% in 10000
CONSTRUÍDO COM SUCESSO (tempo total: 100 minutos 47 segundos)