2.2Matrices.md

2.2 矩阵

矩阵在线性代数中起着核心作用。 它们可用于紧凑地表示线性方程组，此外它们也表示线性函数（线性映射），我们将在后面的2.7节中看到。 在我们讨论这些有趣的话题之前，让我们首先定义矩阵是什么以及我们可以对矩阵进行什么样的操作。 我们将在第4章看到更多矩阵的性质。

定义 2.1 （矩阵）。对于 $ m,n \in \mathbb{N} $，实值 $ (m,n) $ 矩阵（matrix） $ \boldsymbol A $ 是元素 $ a_{ij} $ 的 $ m·n $ 元组，$ i = 1,...,m , j = 1,...,n $，其由$ m $行和$ n $列组成的矩形排序阵列：

$$ \boldsymbol A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \ a_{21} & a_{22} & \cdots & a_{2n} \ \vdots & \vdots & & \vdots \ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}, a \in \mathbb{R}. \tag{2.11} $$

通常 $ (1,n) $ - 矩阵称为行，$ (m,1) $ - 矩阵称为列。 这些特殊矩阵也称为 行/列向量（row/column vectors）。

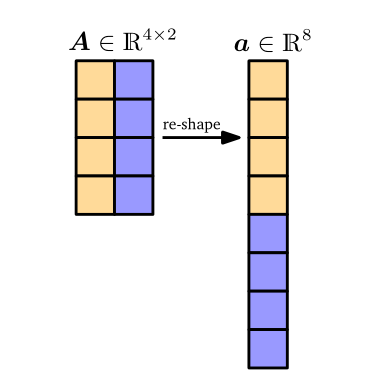
$ \mathbb{R}^{m \times n} $ 是所有实值 $ (m,n) $ 矩阵的集合。 $ \boldsymbol A \in \mathbb{R}^{m \times n} $ 可以等价的表示为将矩阵的所有 $ n $ 列堆叠成一个长的向量 $ \boldsymbol a \in \mathbb{R}^{mn} $ ； 见图 2.4。

图 2.4 通过堆叠其列，矩阵A可以表示为一个长向量a

2.2.1 矩阵加法和乘法

两个矩阵的和 $ \boldsymbol A \in \mathbb{R}^{m \times n}, \boldsymbol B \in \mathbb{R}^{m \times n} $ 被定义为对应元素的和，即，

$$ \boldsymbol A + \boldsymbol B := \begin{bmatrix} a_{11} + b_{11} & \cdots & a_{1n} + b_{1n} \ \vdots \ a_{m1} + b_{m1} & \cdots & a_{mn} + b_{mn} \end{bmatrix} \in \mathbb{R}^{m \times n} \tag{2.12} $$

对于矩阵 $ \boldsymbol A \in \mathbb{R}^{m \times n}, \boldsymbol B \in \mathbb{R}^{n \times k} $ ，乘积 $ \boldsymbol C = \boldsymbol A \boldsymbol B \in \mathbb{R}^{m \times k} $ 的元素 $ c_{ij} $ 计算自

$$ c_{ij} = \sum_{l=1}^{n}{a_{il}b_{lj}}, i = 1,...,m, \ j = 1,...,k \tag{2.13} $$

注意矩阵的大小。 C = np.einsum('il, lj', A, B)

这意味着，为了计算元素 $ c_{ij} $，我们将 $ \boldsymbol A $ 的第 $ i $ 行的元素与 $ \boldsymbol B $ 的第 $ j $ 列的元素相乘，然后将它们相加。 稍后在第3.2节中，我们将称其为相应行和列的 点积（dot produc） 。 在需要明确表示正在执行乘法的情况下，我们使用符号 $ \boldsymbol A \ · \boldsymbol B $ 来表示乘法（明确显示“·”）。

$ \boldsymbol A $ 中有 $ n $ 列，$ \boldsymbol B $ 中有 $ n $ 行，因此我们可以计算 $ a_{il}b_{lj} $，其中 $ l = 1,...,n $。 通常，两个向量 $ \boldsymbol a, \boldsymbol b $ 之间的点积表示为 $ \boldsymbol a^\top \boldsymbol b $ 或 $ \langle \boldsymbol a, \boldsymbol b \rangle $。

备注 。 只有当它们的“相邻”维度匹配时，矩阵才能相乘。 例如，一个 $ n \times k $ 矩阵 $ \boldsymbol A $ 可以乘以一个 $ k \times m $ 矩阵 $ \boldsymbol B $ ，只能从左侧相乘：

$$ \underbrace{\boldsymbol A}{n \times k} \ \underbrace{\boldsymbol B}{k \times m} = \underbrace{\boldsymbol C}_{n \times m} \tag{2.14} $$

如果 $ m \not= n $，则乘积 $ \boldsymbol {BA} $ 未定义，因为相邻维度不匹配。

备注 。 矩阵乘法并非定义为矩阵逐元素的运算，即 $ c_{ij} \not= a_{ij}b_{ij} $（即使 $ \boldsymbol A、\boldsymbol B $ 的大小相同）。 当我们将（多维）数组彼此相乘时，这种逐元素乘法经常出现在编程语言中，称为 哈达玛乘积（Hadamard product）。

例 2.3 $$ \rm 对于 \ \boldsymbol A = \begin{bmatrix} 1 & 2 & 3 \ 3 & 2 & 1 \end{bmatrix} \in \mathbb{R}^{2 \times 3}, \ \boldsymbol B = \begin{bmatrix} 0 & 2 \ 1 & -1 \ 0 & 1 \end{bmatrix} \in \mathbb{R}^{3 \times 2}, \ \rm 可以获得 $$ $$ \boldsymbol {AB} = \begin{bmatrix} 1 & 2 & 3 \ 3 & 2 & 1 \end{bmatrix} \begin{bmatrix} 0 & 2 \ 1 & -1 \ 0 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 3\ 2 & -5 \end{bmatrix} \in \mathbb{R}^{2 \times 2} \tag{2.15}$$ $$ \boldsymbol {BA} = \begin{bmatrix} 0 & 2 \ 1 & -1 \ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \ 3 & 2 & 1 \end{bmatrix} = \begin{bmatrix} 6 & 4 & 2\ -2 & 0 & 2 \ 3 & 2 & 1 \end{bmatrix} \in \mathbb{R}^{3 \times 3} \tag{2.16} $$

从这个例子中，我们已经可以看出矩阵乘法是不可交换的，即 $ \boldsymbol {AB} \not = \boldsymbol {BA} $； 另请参见图 2.5 中的说明。

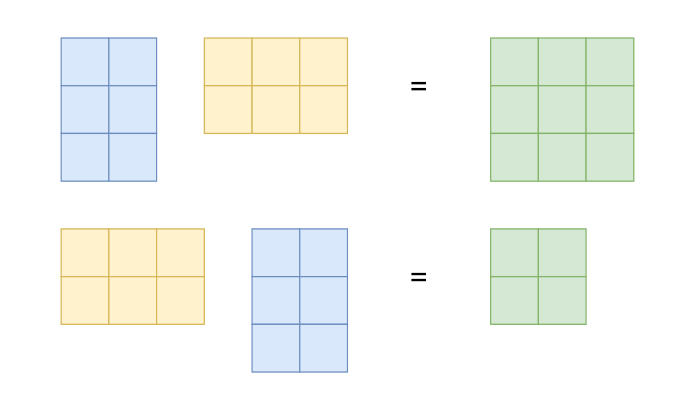
图 2.5 即使矩阵乘法 AB 和 BA 有意义，结果的维度也可能不同。

定义 2.2 （单位矩阵）。 在 $ \mathbb{R}^{n \times n} $ 中，我们将 单位矩阵（identity matrix） 定义为对角线上为 $ 1 $，其他地方为 $ 0 $ 的 $ n \times n $ 矩阵。

$$ \boldsymbol I_n := \begin{bmatrix} 1 & 0 & \cdots & 0 & \cdots & 0 \ 0 & 1 & \cdots & 0 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 1 & \cdots & 0 \ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \ 0 & 0 & \cdots & 0 & \cdots & 1 \end{bmatrix} \in \mathbb{R}^{n \times n} \tag{2.17} $$

到目前我们定义了矩阵乘法、矩阵加法和单位矩阵，让我们看看矩阵的一些性质：

• 结合律： $$ \forall \boldsymbol A \in \mathbb{R}^{m \times n}, \ \boldsymbol B \in \mathbb{R}^{n \times p},\ \boldsymbol C \in \mathbb{R}^{p \times q} :\ (\boldsymbol{AB})\boldsymbol C = \boldsymbol A (\boldsymbol{BC}) \tag{2.18} $$

• 交换律：

$$ \forall \boldsymbol {A,B} \in \mathbb{R}^{m \times n}, \ \boldsymbol {C,D} \in \mathbb{R}^{n \times p}: $$ $$ (\boldsymbol A + \boldsymbol B)\boldsymbol C = \boldsymbol{AC} + \boldsymbol{BC} \tag{2.19a} $$ $$ \boldsymbol A (\boldsymbol C + \boldsymbol D) = \boldsymbol{AC} + \boldsymbol{AD} \tag{2.19b} $$

• 与单位矩阵相乘：

$$ \forall \boldsymbol A \in \mathbb{R}^{m \times n}: \ \boldsymbol {I_m A} = \boldsymbol {A I_n} = \boldsymbol A \tag{2.20} $$

请注意，对于 $ m \not = n $，$ \boldsymbol I_m \not = \boldsymbol I_n $

2.2.2 逆和转置

定义 2.3 （逆）。对于一个方阵 $ \boldsymbol A \in \mathbb{R}^{n \times n} $，令矩阵 $ \boldsymbol B \in \mathbb{R}^{n \times n} $ 具有 $ \boldsymbol {AB} = \boldsymbol I_n = \boldsymbol {BA} $ 的性质。 $ \boldsymbol B $ 称为 $ \boldsymbol A $ 的 逆（inverse） ，用 $ \boldsymbol A^{-1} $ 表示。

方阵具有相同的列数和行数。

不幸的是，并非每个矩阵 $ \boldsymbol A $ 都具有逆 $ \boldsymbol A^{-1} $。 如果这个逆确实存在，则 A 称为 正则/可逆/非奇异（regular/invertible/nonsingular），否则称为 奇异/不可逆（singular/noninvertible）。 当矩阵逆存在时，它是唯一的。 在 2.3 节中，我们将讨论通过求解线性方程组来计算矩阵逆的一般方法。

备注（存在 2 × 2 矩阵的逆矩阵）。 考虑一个矩阵:

$$ \boldsymbol A := \begin{bmatrix} a_{11} & a_{12} \ a_{21} & a_{22} \end{bmatrix} \in \mathbb{R}^{2 \times 2} \tag{2.21} $$

如果我们将 $ \boldsymbol A $ 乘以

$$ \boldsymbol A^{'} := \begin{bmatrix} a_{22} & -a_{12} \ -a_{21} & a_{11} \end{bmatrix} \tag{2.22} $$

我们得到

$$ \boldsymbol {AA^{'}} = \begin{bmatrix} a_{11}a_{22} - a_{12}a_{21} & 0 \ 0 & a_{11}a_{22} - a_{12}a_{21} \end{bmatrix} = a_{11}a_{22} \boldsymbol I \tag{2.23} $$

因此

$$ \boldsymbol A^{-1} = \frac{1}{a_{11}a_{22} - a_{12}a_{21}}\begin{bmatrix} a_{22} & -a_{12} \ -a_{21} & a_{11} \end{bmatrix} \tag{2.24} $$

当且仅当 $ a_{11}a_{22} - a_{12}a_{21} \not= 0 $。在4.1节中，我们将看到 $ a_{11}a_{22} - a_{12}a_{21} $ 是 2×2 矩阵的行列式。 此外，我们通常可以使用行列式来检查矩阵是否可逆。

例 2.4（逆矩阵） 矩阵 $$ \boldsymbol A = \begin{bmatrix} 1 & 2 & 1 \ 4 & 4 & 5 \ 6 & 7 & 7 \end{bmatrix}, \ \boldsymbol B = \begin{bmatrix} -7 & -7 & 6 \ 2 & 1 & -1 \ 4 & 5 & -4 \end{bmatrix} \tag{2.25} $$ 互为逆矩阵，因为 $ \boldsymbol {AB} = \boldsymbol I = \boldsymbol {BA} $ 。

定义 2.4 （转置）。对于 $ \boldsymbol A \in \mathbb{R}^{m \times n} $，矩阵 $ \boldsymbol B \in \mathbb{R}^{n \times m} $ 且 $ b_{ij} = a_{ji} $ 称为 $ \boldsymbol A $ 的 转置（transpose）。 我们写 $ \boldsymbol B = \boldsymbol A^{\top} $。

一般情况下，可以通过将 $ \boldsymbol A $ 的列写为 $ \boldsymbol A^{\top} $ 的行来获得 $ \boldsymbol A^{\top} $ 。以下是逆和转置的重要性质：

$$ \boldsymbol {AA^{-1}} = \boldsymbol I = \boldsymbol {A^{-1}A} \tag{2.26} $$ $$ \boldsymbol {(AB)^{-1}} = \boldsymbol {B^{-1}A^{-1}} \tag{2.27} $$ $$ \boldsymbol {(A + B)^{-1}} \not= \boldsymbol {A^{-1} + B^{-1}} \tag{2.28} $$ $$ (\boldsymbol {A^{\top})^{\top}} = \boldsymbol A \tag{2.29} $$ $$ \boldsymbol {(A + B)^{\top}} = \boldsymbol {A^{\top} + B^{\top}} \tag{2.30} $$ $$ \boldsymbol {(AB)^{\top}} = \boldsymbol {B^{\top}A^{\top}} \tag{2.31} $$

矩阵 $ \boldsymbol A $ 的主对角线是全部 $ A_{ij} $ 的集合，其中 $ i = j $。 (2.28) 的标量情况是 $ \frac{1}{2 + 4} = \frac{1}{6} \not= \frac{1}{2} + \frac{1}{6} $

定义 2.5 （对称矩阵）。如果 $ \boldsymbol A = \boldsymbol A^{\top} $， 则矩阵 $ \boldsymbol A \in \mathbb{R}^{n \times n} $ 是 对称矩阵（symmetric matrix）。

请注意，只有 $ (n, n) $ 矩阵才可以是对称的。通常，我们称 $ (n, n) $ 矩阵也为 方阵（square matrix），因为它们具有相同的行数和列数。此外，如果 $ \boldsymbol A $ 是可逆的，那么 $ \boldsymbol A^{\top} $ 也是可逆的，并且 $ (\boldsymbol A^{-1})^{\top} = (\boldsymbol A^{\top})^{-1} =: \boldsymbol A^{\top} $ 。

备注（对称矩阵的和与乘积）。 对称矩阵 $ \boldsymbol {A,B} \in \mathbb{R}^{n \times n} $ 的总和总是对称的。 然而，虽然他们的乘积有意义，但它通常不是对称的：

$$ \begin{bmatrix} 1 & 0 \ 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \ 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 \ 0 & 0 \end{bmatrix} \tag{2.32} $$

2.2.3 乘以标量

让我们看看当矩阵乘以标量 $ \lambda \in \mathbb{R} $ 时会发生什么。让 $ \boldsymbol A \in \mathbb{R}^{m \times n} $ 和 $ \lambda \in \mathbb{R} $，然后 $ \lambda \boldsymbol A = \boldsymbol K, K_{ij} = \lambda a_{ij} $ 。 实际上， $ \lambda $ 缩放了 $ \boldsymbol A $ 的每个元素。 对于 $ \lambda,\psi \in \mathbb{R} $，以下成立：

• 结合律 $$ (\lambda \psi)\boldsymbol C = \lambda(\psi \boldsymbol C), \ \boldsymbol C \in \mathbb{R}^{m \times n} $$

• $ \lambda (\boldsymbol {BC}) = (\lambda \boldsymbol B) \boldsymbol C = \boldsymbol B (\lambda \boldsymbol C) = (\boldsymbol {BC}) \lambda, \ \boldsymbol B \in \mathbb{R}^{m \times n}, \ \boldsymbol C \in \mathbb{R}^{n \times k} $ 。请注意，这意味着我们可以随意移动标量值。

• $ (\lambda \boldsymbol C)^{\top} = \boldsymbol C^{\top} \lambda^{\top} = \boldsymbol C^{\top} \lambda = \lambda \boldsymbol C^{\top} $ ， 因为对于所有的 $ \lambda \in \mathbb{R}, \ \lambda = \lambda^{\top} $ 。

• 分配律 $$ (\lambda + \psi) \boldsymbol C = \lambda \boldsymbol C + \psi \boldsymbol C, \ \boldsymbol C \in \mathbb{R}^{m \times n} $$ $$ \lambda (\boldsymbol B + \boldsymbol C) = \lambda \boldsymbol B + \lambda \boldsymbol C, \ \boldsymbol {B,C} \in \mathbb{R}^{m \times n} $$

例 2.5（分配律） 如果我们定义 $$ \boldsymbol C := \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}, \tag{2.33} $$ 那么对于任何 $ \lambda, \psi \in \mathbb{R} $ 我们得到 $$ (\lambda + \psi)\boldsymbol C = \begin{bmatrix} (\lambda + \psi)1 & (\lambda + \psi)2 \ (\lambda + \psi)3 & (\lambda + \psi)4 \end{bmatrix} = \begin{bmatrix} \lambda + \psi & 2\lambda + 2\psi \ 3\lambda + 3\psi & 4\lambda + 4\psi \end{bmatrix} \tag{2.34a} $$ $$ = \begin{bmatrix} \lambda & 2\lambda \ 3\lambda & 4\lambda \end{bmatrix} + \begin{bmatrix} \psi & 2\psi \ 3\psi & 4\psi \end{bmatrix} \tag{2.34b} = \lambda \boldsymbol C + \psi \boldsymbol C $$

2.2.4 线性方程组的紧凑表示

如果我们考虑线性方程组

$$ 2x_1 + 3x_2 + 5x_3 = 1 \\ 4x_1 - 2x_2 - 7x_3 = 8 \\ 9x_1 + 5x_2 - 3x_3 = 2 \tag{2.35} $$

并使用矩阵乘法的规则，我们可以将这个方程组写成更紧凑的形式

$$ \begin{bmatrix} 2 & 3 & 5 \ 4 & -2 & -7 \ 9 & 5 & -3 \end{bmatrix} \begin{bmatrix} x_1 \ x_2 \ x_3 \end{bmatrix} = \begin{bmatrix} 1 \ 8 \ 2 \end{bmatrix} \tag{2.36} $$

请注意，$ x_1 $ 缩放第一列，$ x_2 $ 缩放第二列，$ x_3 $ 缩放第三列。

通常，线性方程组可以用其矩阵形式紧凑地表示为 $ \boldsymbol {Ax} = \boldsymbol b $； 见 (2.3)，乘积 $ \boldsymbol {Ax} $ 是 $ \boldsymbol A $ 的列的（线性）组合。 我们将在 2.5 节中更详细地讨论线性组合。