原文:Deep Exploration Into Python: Let's Review The Dict Module
Dictobject.c是Python的dict对象背后的模块。它非常常用,但有一些鲜为人知的秘密,这些秘密对于了解最佳性能非常有用。
本文是旨在深入Python解释器系列的第一篇。Python是一门成熟的语言,它的提交可以追溯到1990年八月份。一路走来,开发者们已经为贡献发展了一系列的流程,从而允许他们对几个错误/问题相对快速地处理推进。
在这个系列中,我们将会看看Python各种各样的模块和功能块。我们将会看到设计选择,它们的影响及其演变。我们还会看到语言本身的设计,了解解释器一路解析语言到主要的eval循环。最后,我们将尝试提供由对该语言的进一步的理解所得到的实际小贴士。
Python的cpython实现 (这是大多数机器上的标准)已经从它的出生地Mercurial移植到了GitHub上。我想,它也在SVN下待过一段时间,但工程师们设法保存(大部分)的提交日志。
如果你之前从未见过,git提供了一个非常赞的特性,可以查看单一文件的提交历史。这篇文章部分来源于下面这条命令:
我检查了Objects/dictobject.c大致十年的提交历史,带来历史考量的有趣花絮,以及dict算法现代实现的概述。(如果你发现任何不准确的地方或者勘误,请给我留言。) (Ele注:翻译过程中有任何不准确或错误,也欢迎提issue,O(∩_∩)O~)
dict接口多年来不断变化。实际上有一段很长的时间"for k in d"是不存在的!看看下面这个易得的时间表。
| .values(), .keys(), .items() | May 19, 1993 |
|---|---|
| .clear() | March 21, 1997 |
| .copy() | May 28, 1997 |
| .merge(), .update() | June 2, 1997 |
| .pop() | October 6, 1997 |
| .first() | November 30, 2000 |
| .popitem() | December 12, 2000 |
| for k in d | April 20, 2001 |
| key in d, key not in d | April 20, 2001 |
| .iterkeys(), .iteritems(), .itervalues() | May 1, 2001 |
| d1 != d2, d1 == d2 | May 8, 2001 |
| dict(['foo', 'bar']) | October 26, 2001 |
dict是mapping类型的泛化。mapping类型已经和我们永别了,但根据官方文档,dict仍然是Python中它们唯一的实例。实际上,你可以找到冲突文档,不过,我倾向于同意这种说法。如果mapping被定义为映射不可变的键到值的对象,那么collections.OrderedDict和collections.defaultdict也符合条件。
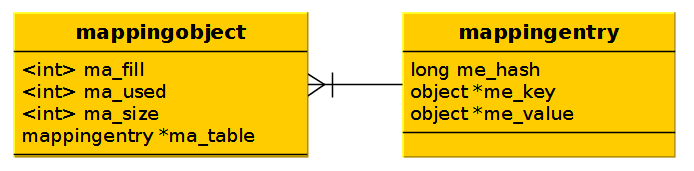
早期,有一个mappingobject.c文件,实际上已经_重命名_为dictobject.c。
无论如何,很高兴知道这些 —— 但让我们看看关于这个模块的设计决定,以了解具体细节。
Python字典的实现中有大量的语义。在接下来的小节中,我们将讨论到字典基本方法的设计选择和实现细节。我们将_几乎_了解到字典现今所知的完整实现。我为将来的文章留下了一些东西没提(例如,分割字典盒指定类型的实现)。
Python使用哈希表来获得随机访问键的O(1)查找。mapping对象的另一个最常见的选择是二叉树查找。Python选择哈希表而不是B树是非常明智的。
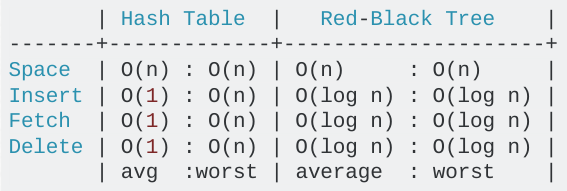
Python的字典作为可调整大小的哈希表实现。与B树相比,在大多数的情况下,对于查找(迄今为止最常见的操作)会获得更好的性能,并且实现更简单。--python.org
事实上,你可以非常清楚的看到性能差异:
@amon 在stackexchange.com上 / 通过programmers.stackexchange.com
冲突的思想是可以创建或打破哈希表实现的一个概念。为你的使用情况妥善处理这些可以让你的方法非常的快。处理不当,则会让操作非常慢。
Python的哈希处理冲突的方法有问题历史,实现一次,然后用于Python 2.7之前的所有版本。检查这些变化集是了解关于解决冲突的不同设计抉择的缺点的一种显著方法。要了解Python处理哈希表的方法,知道一点术语是很重要的:
- 哈希(hash): 通过哈希算法映射到键的一个数值。也就是说,f(key) -> hash
- 槽(slot): 一个字典键值可保存的哈希表中的一个空位置
- 哑键(dummy key): 当删除字典的一个键值时,不留下一个空的_槽_。这将使得不可能找到其他的键(稍后详述)。我们留下一个_哑键_来代替。
- NULL键(NULL key): 在表中的一个_槽_被键值对使用/占据之前,一个键所拥有的值
- 项(entry): 占据一个_槽_的哈希值和键值对
mapping对象是mapping项的容器。它维护了到_ma_fill_ (非NULL键 —— 例如,哑键+项 —— 的数目); ma_used (非NULL键,非哑键的数目); 和_ma_size_(一个表示基础表的大小(分配的内存)的素数)的引用。
Python查找算法的核心是一个名为"lookmapping"的方法。Guido在他的提交中这样描述它:
T所有操作都使用的基础查找函数。这实质上是来自Knuth Vol. 3, Sec. 6.4的算法D。开放寻址优于链接,因为链接的链路开销将是巨大的。
现在我们有了构造块,让我们来了解下开放寻址和链接之间的差别。我会在下面解释,但是鼓励你看看上面链接的维基百科页面。如果你有兴趣,那么Knuth的书也可以在Amazon上找到。
开放寻址
在_开放寻址_中,分配整个地址空间。这包括可以直接插入到空间中的所有项的空间,以及那些通过冲突序列找到它们的槽的项的空间。
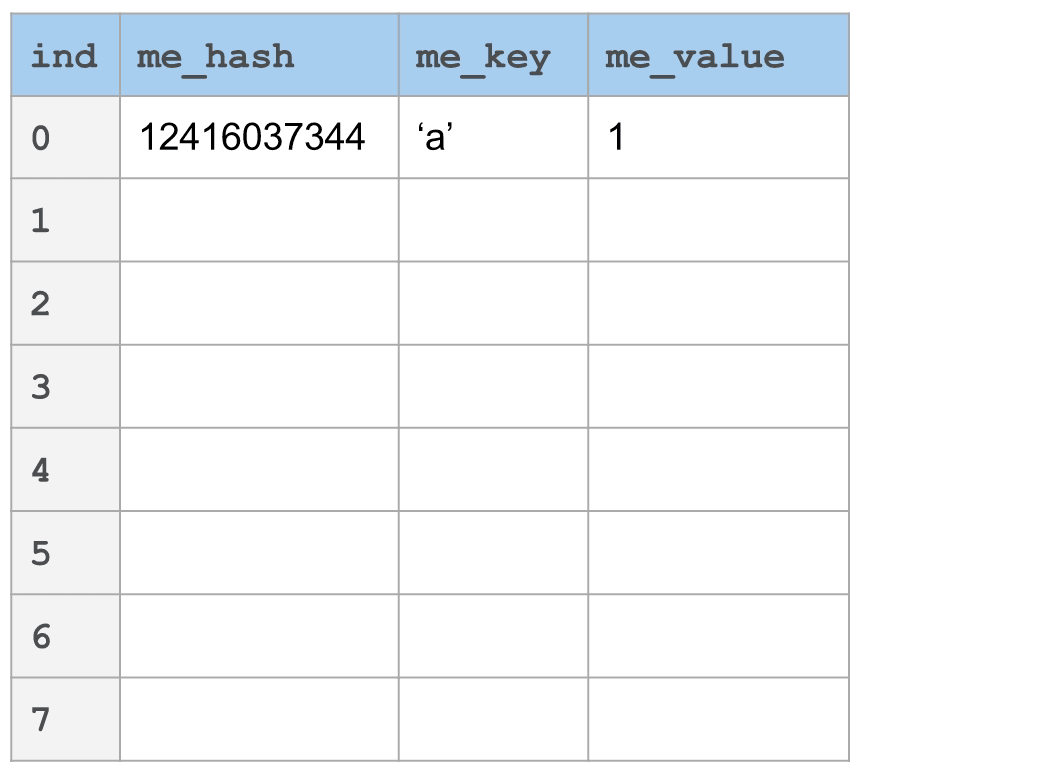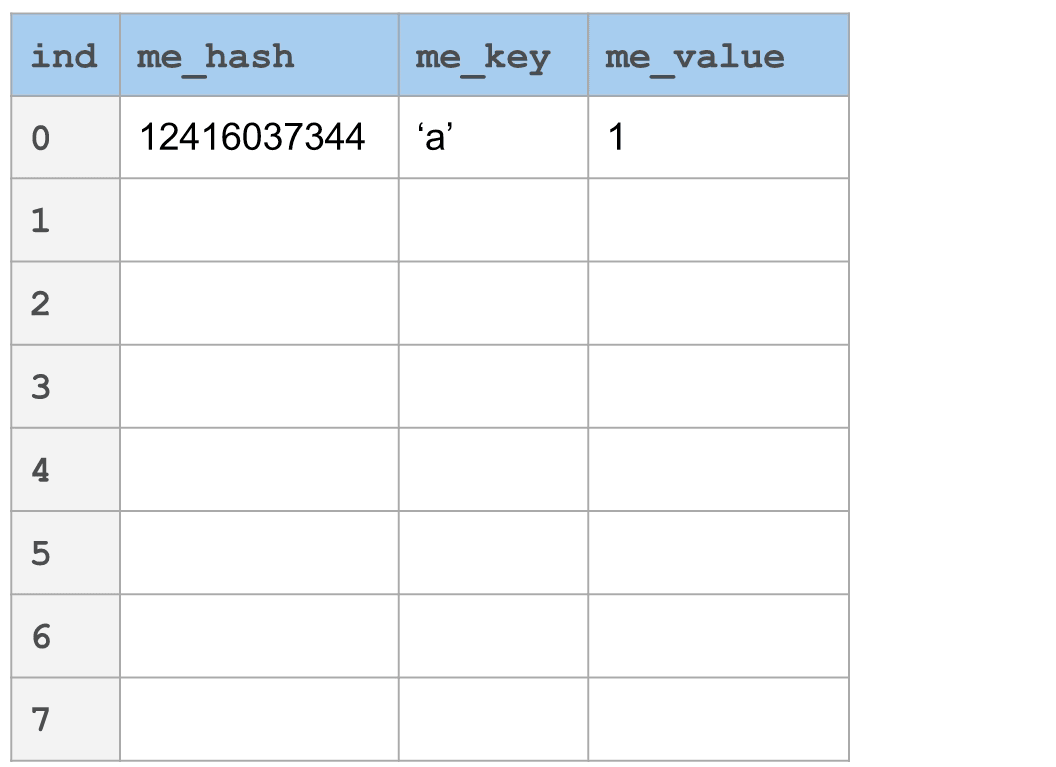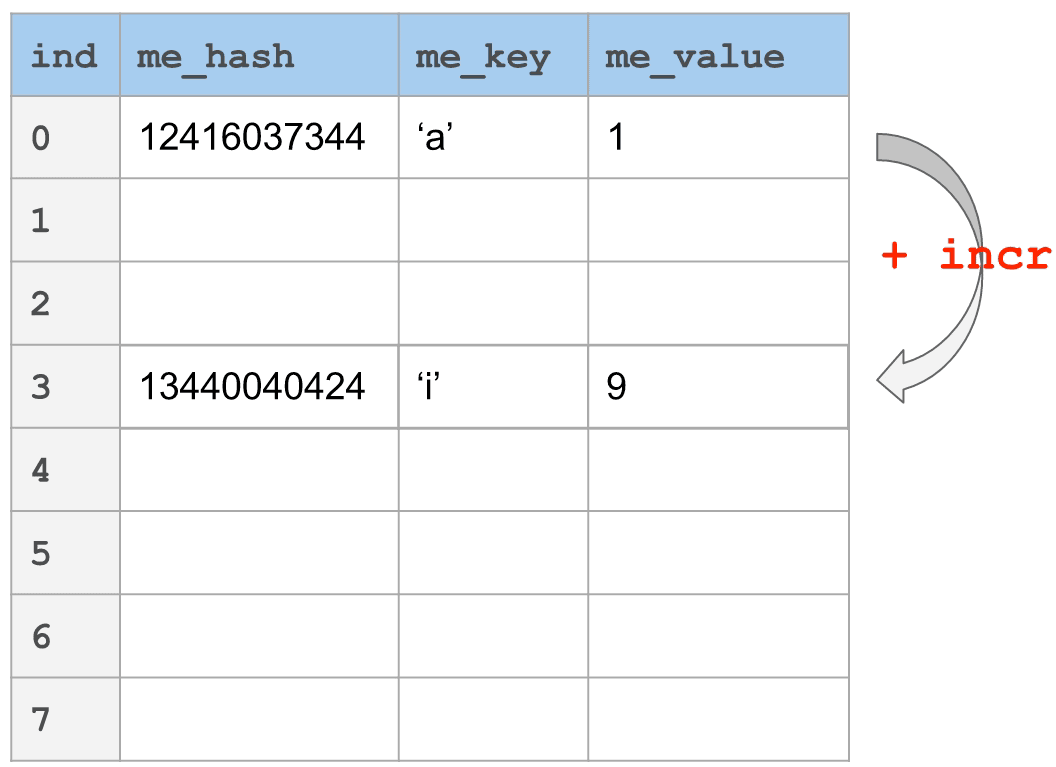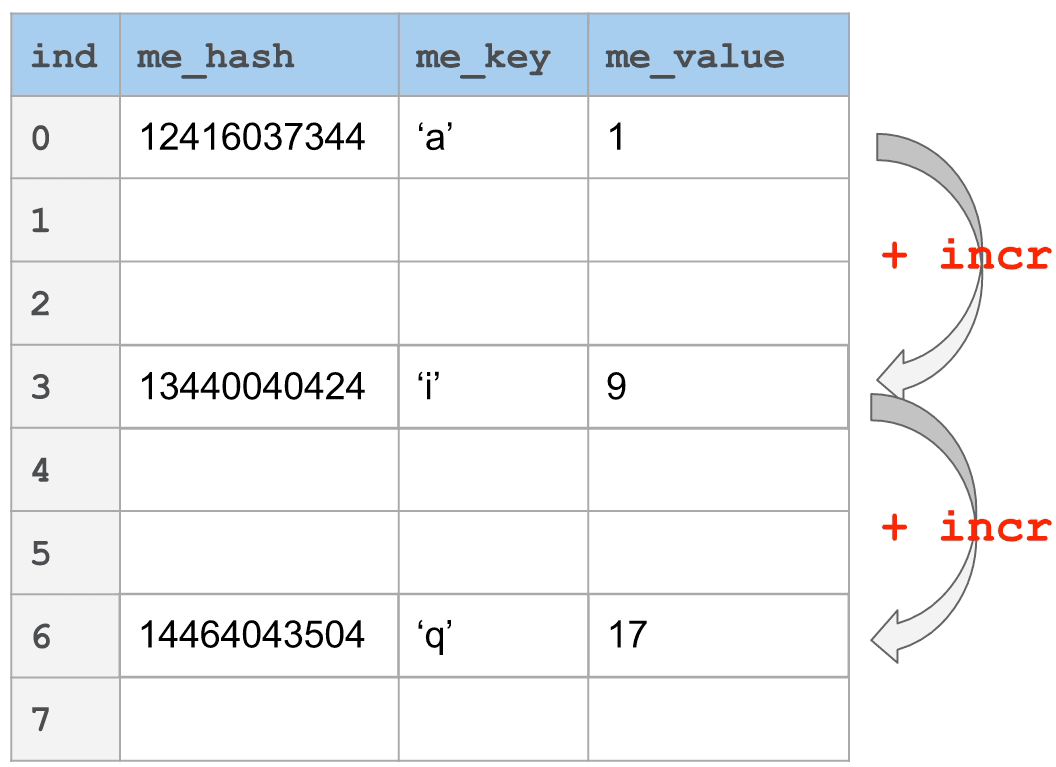
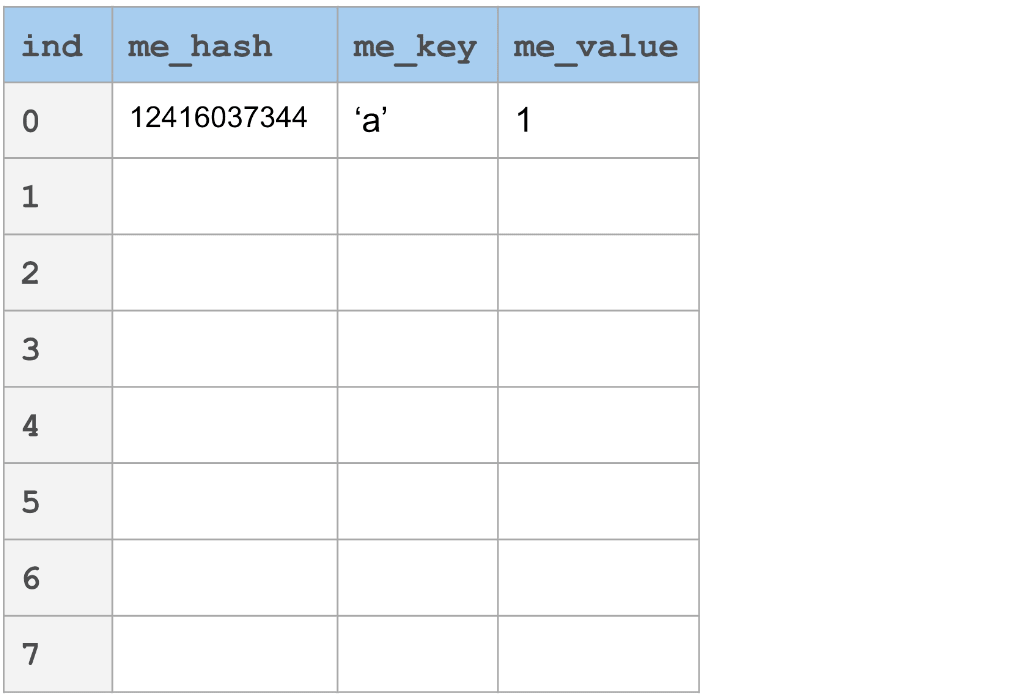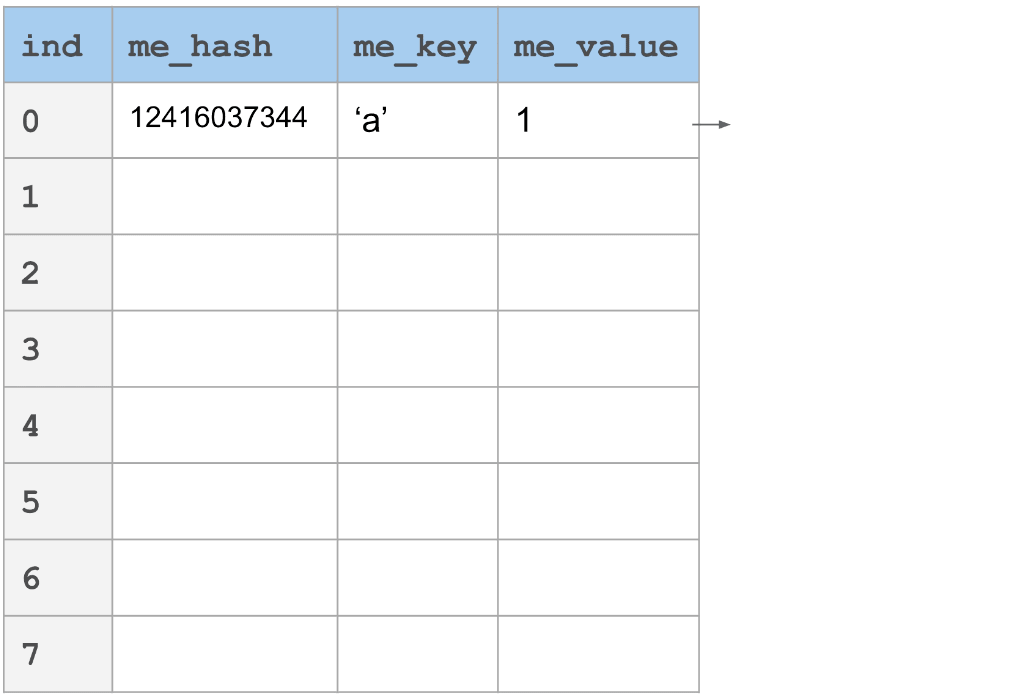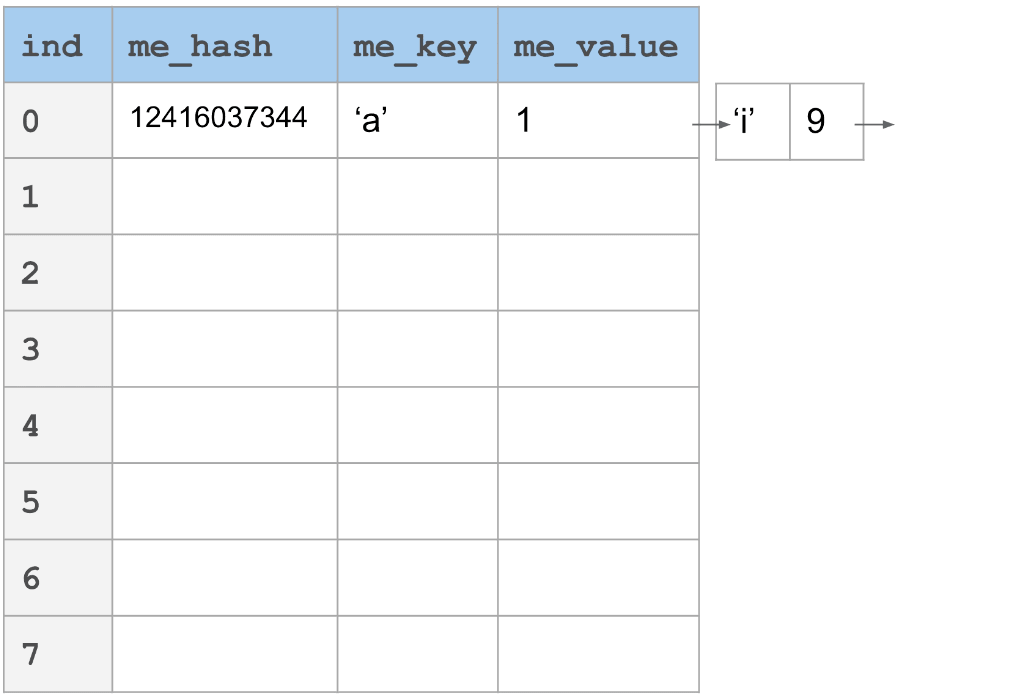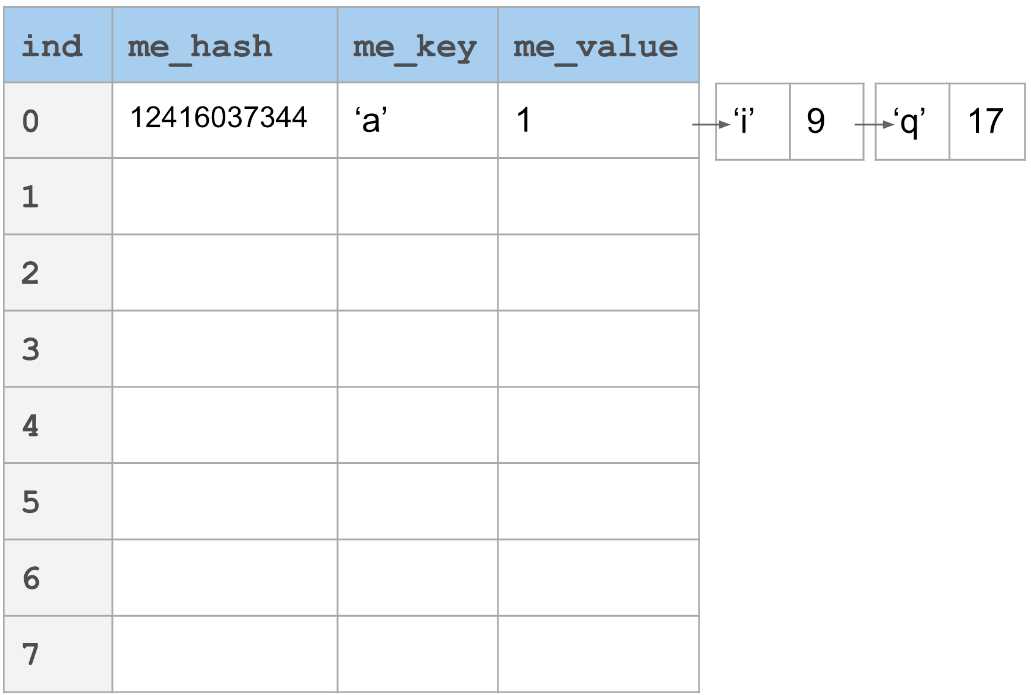
在下图中,你将看到一个_线性探针_的例子。键'a'哈希到12416037344。以表大小(8)为模,我们发现它落到槽0中。如果现在我们想要添加"i",它_也_映射到槽0,那该怎么办呢?只需简单地根据"incr"向前跳过一定数量的槽。在这个情况下,incr设为3。每个会与槽0冲突的键将会通过n倍的incr找到它的位置,其中,n是到那个点发生冲突的数量。
我们在这里描述的场景在最好的情况下是O(1)次查找,最坏的情况下是O(n)次查找。在最坏的情况下,它相当于线性搜索空间。
链接
_开放寻址_与_链接_不同的地方在于内存的分配。冲突发生的时候,不是探索新的槽,而是将其附加到一个链表中。这在最好的情况下也是O(1)次查找,最坏的情况下也是O(n)次查找。而主要的差别是分配开销。在链接中,我们需要为每个在插入操作中发生的冲突进行额外的在堆中分配元素的操作。
聚集
在许多方面,一个哈希表实现的质量归结于它冲突解决机制的质量。如果键在表中变得过于紧密,最终我们会处在称之为“聚集”的处境中。聚集会使得对于一系列的键,比平常的冲突更多,因此,通常不可取。
勘误:如reddit上的用户ggchappell所指出的,这里的incr公式应该是(3 * hash + 1) % 8。
Python开始实际的探测公式如上所示:(3 * hash + 1) % table_size。上面描述的是真实的场景,其中,我们会有一个线性聚集以及非常差的查找性能。
好啦。不过说真的。有什么问题呢?嗯,在1997年1月16日,Guido写了这个,确认dict查找背后的核心算法必须是AFAP。
显然,在这个时候,它并不是。
在GCC和clang的现代实现中,你会发现优化了模运算。但是,曾几何时,它实际上分解成了这个公式:
…其中,一个操作中出现了三种操作。哇!为了摆脱这点,并更进一步使用更少更快的操作,Guido (在其他贡献者的帮助下)提交了一个新的实现了有限域的查找算法用于随机查找。This decreased the collision rate substantially.
作为侧面说明:在Python中,模操作_仍然_比按位操作(提供类似功能)慢一点。
无论如何,有限域之后,lookmapping方法有了一系列的小变化,这导致了100%的速度提升。看看这个提交。真真杀千刀的。
对于那些在找出改了什么有困难的人,他们
- 将"if"语句序列改成了"if/else";
- 延迟计算"哈希值"直到需要;以及
- 将"哈希值"存储在寄存器中,而不是堆栈中。
在这些改动几年内在社区中有了一些时间之后,有人在python-dev列表中提出,当计算一个项应该放在哪个槽的时候,并不是所有的哈希值比特都实际发挥作用。
尤其是一个导致所有的项都落在相同的槽中的集合。这是由[i << 16 for i in range(20000)]定义的集合。考虑下cpython项目下面的提交信息:
如果表大小每次都加倍(对于上面提到的集合),那么每个单一的项都被放在槽0.这非常糟糕。为了解决这个问题,Tim Peters在2001年五月提交了一个特性,它使用多项式除法来将哈希值的更多位数与每个后续的冲突进行合并。
我想团队认为这有点难以理解。不清楚为什么,但是一个月后,也就是2001年6月1日,多项式除法方法被一个很简单的递归函数取而代之。
引用dictobject.c中的注释:此时,冲突解决的前半部分是通过这个递归访问表索引……
j = ((5*j) + 1) mod 2**i
对于range(2i)中的任何初始j,重复i次生成range(2i)中的每个int。
再次来自dictobject.c:该策略的另一半是使用哈希码的其他位。这通过初始化一个(无符号)变量"perturb"为完整的哈希码,并将递归改成下面这样来做到:
j = (5*j) + 1 + perturb;
perturb >>= PERTURB_SHIFT;
The next table index is just j % 2**i
此时,固化了以下规则:
- 表大小是2**n,最小值是8个槽。
- 表索引是使用与表大小中比特相同数目的哈希比特数,根据哈希值计算的。
- 负载因素 (已填充槽的数目) 必须低于2/3表大小,否则表大小调整为2的下一个幂。
好了。我们已经看了很多的实现了。从中获得一些你可以在日常中使用的实用的东西会更好。下面是从我们审查的东西中直接获得的几件事。
默认的表大小是8个元素。由于加载率必须保持低于2/3,因此在增加第5个元素的时候,我们的表将会调整大小。让我们看看实例化两个4元素字典对比一个8元素字典有什么区别。
你可能你期望由于创建两个独立的容器有关的开销,两个4元素的字典花的时间会长点。但情况并非如此。考虑以下代码:
输出显示为
…暗示因避免重新调整大小,有额外30%的性能收益。
现在,用Donald Knuth的话来说,“过早的优化是一切罪恶的根源。”我当然不是主张分裂逻辑相关的字典以获得速度增益。如果你担心这样小的速度提升,那么你应该考虑使用pypy或者完全另一种语言。另一方面,例如,如果你进行数据库查询,那么你可能会考虑将SELECT *替换成所需的元素(如果没有的话)。
我们看到对于那些比特位移了16次的整数集,有500倍的提升。那么32次呢?听上去很疯狂,不是吗?1 << 32处在4B范围内。这很大,但并不是天文数字。事实上,分配用户ID的一些方案就用了这个范围。
考虑下面的代码:
你可能从上下文就可以猜到了,带有大键的dict花了需要大约30%更长的世界来分配,这说明冲突的几率高得多。
由于dict的大小调整计划遵循标准的指数(2**n)过程,因此,比2/3略大的dict在调整大小的时候,会使用相当多的额外空间。
重新调整dict对象大小的代码。
可能有人告诉过你,dict的顺序是无法_保证的_。这是对的!但实际上是……有点儿。cpython中计算字典键放置元素的方法是确定的。这意味着每次传递相同的值将会获得相同的结果。
让元素乱了次序的原因实际上是dict的_历史_。考虑以下。
在这个例子中,我们有两个键:1111和111。由于我们的表大小是8 (新的dict的默认大小),我们知道将一个元素放进表的时候只会考虑三个位(因为对于三个位,只有8种可能的组合)。
知道了这一点,我们可以进行哈希了。每个键的最后三个位是111,这意味着我们一定会有冲突。以一种次序将其添加到dict a,以另一种次序将其添加到dict b,保证了第一个元素获得这个dict中的第一个槽。当我们尝试添加下一个元素,将会有冲突,此时它将会被放在表中另一个槽(在这个例子中,恰好是第一个槽之前)。
当我们打印出这个dict的键时,可以看到,它们的次序乱了。虽然,这种行为是一致的,并且可重现。只要我们以_相同的_次序添加元素,那么对于写这篇文章的时候Python 2.7和3.x的最新版本来说,次序将保持一致。
对那些没试过的人来说,当你试图使用一个可变类型作为dict的键时,会发生以下情况:
这里的问题源于这样的事实:默认情况下,可变类型没有__hash__()方法。对于给定的容器,对这种情况并无_内在_原因,但当你考虑到__hash__()是用来干嘛的,会看到理由很充分。
如果你把一个列表当成字典键,接着改变它,那么哈希值会发生改变。这意味着未来对这个元素的查找将会失败,因为传递该值用于查询将会得到一个不同的哈希值。来看个例子。
首先,必须用一个扩展list的类,它定义了__hash__()方法。这会做的不错。
现在,我们可以将_我们的_列表当成一个可变字典键了!hlist是我们的可哈希列表。hlist2是一个包含相同元素的_单独的_可哈希列表。
设置d[hlist] = 'a',我们可以用hlist或者新的列表hlist2(包含相同次序的相同值)来查找值'a'。
这是因为,根据值,列表是相同的,并且,在__hash__()下,它们有相同的输出。现在,让我们来改变hlist。需要明确的是:生成a的d的键_是_hlist。它不是hlist的_值_,而是hlist本身。
然后,_通过引用_修改hlist将会有一定的不良影响。这将会导致hlist的_值_和_hash_发生改变。虽然,它已经在分配给它的槽里面了,这将很可能不恰当地赋给它新的哈希值和值。
所以,正如你所想的那样,附加4到hlist引发查找错误。在d中,它仍然作为一个键存在,但是现在,它有了一个不同的哈希值和不同的值。
当我们通过原始变量hlist进行查找的时候,计算得到一个错误的哈希值,看起来hlist不再存在在d中。当我们通过原始值hlist2进行查找的时候,根据它的哈希值,找到正确的槽,但值并不匹配,所以看起来hlist2也不在d中。