05.String-Horspool.md

1.1 Horspool 算法介绍

Horspool 算法：是一种在字符串中查找子串的算法，它是由 Nigel Horspool 教授于 1980 年出版的，是首个对 Boyer Moore 算法进行简化的算法。

• Horspool 算法思想：对于给定文本串 $T$ 与模式串 $p$，先对模式串 $p$ 进行预处理。然后在匹配的过程中，当发现文本串 $T$ 的某个字符与模式串 $p$ 不匹配的时候，根据启发策略，能够尽可能的跳过一些无法匹配的情况，将模式串多向后滑动几位。

可以看出，Horspool 算法思想和 Boyer Moore 算法思想是一致的。Horspool 算法是在 Boyer Moore 算法思想基础上改进了「坏字符规则」。当文本串 $T$ 中某个字符跟模式串 $p$ 的某个字符不匹配时，可以模式串 $p$ 快速向右移动。

遇到不匹配字符时，可以根据以下两种情况向右快速进行移动：

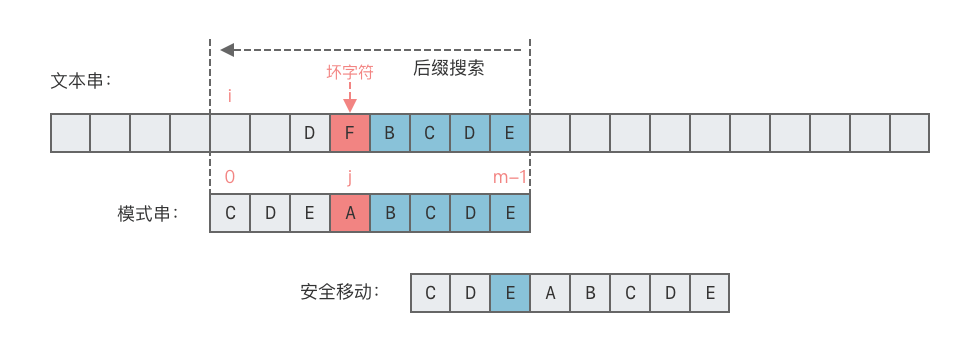
• 情况 1：文本串 $T$ 中与模式串 $p$ 尾部字符 $p[m - 1]$ 对应的字符 $T[i + m - 1]$ 出现在模式串 $p$ 中。
  • 这种情况下，可将 $T[i + m - 1]$ 与模式串中最后一次出现的该字符对齐，如下图所示。
  • 向右移动位数 = 模式串最后一个字符的位置 - T[i + m - 1] 在模式串中最后一次出现的位置。
  • 注意：模式串最后一个字符的位置其实就是「模式串长度 - 1」。

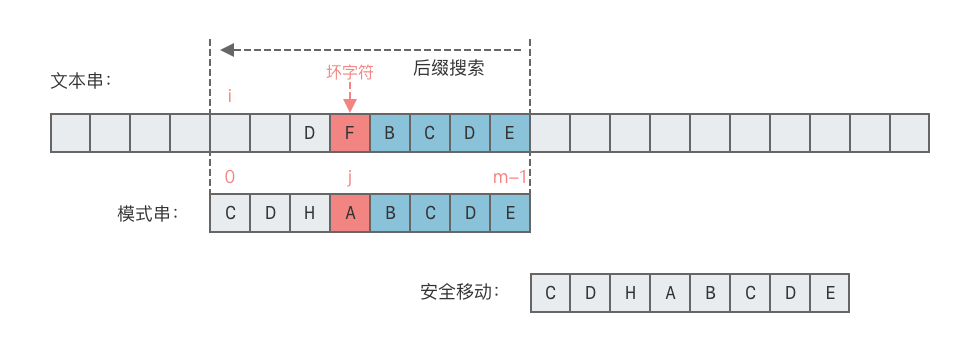
• 情况 2：文本串 $T$ 中与模式串 $p$ 尾部字符 $p[m - 1]$ 对应的字符 $T[i + m - 1]$ 没有出现在模式串 $p$ 中。
  • 这种情况下，可将模式串整个右移，如下图所示。
  • 向右移动位数 = 整个模式串长度。

2. Horspool 算法步骤

整个 Horspool 算法步骤描述如下：

1. 计算出文本串 $T$ 的长度为 $n$，模式串 $p$ 的长度为 $m$。
2. 先对模式串 $p$ 进行预处理，生成后移位数表 $bc\underline{\hspace{0.5em}}table$。
3. 将模式串 $p$ 的头部与文本串 $T$ 对齐，将 $i$ 指向文本串开始位置，即 $i = 0$。$j$ 指向模式串末尾位置，即 $j = m - 1$，然后从模式串末尾位置开始比较。
   1. 如果文本串对应位置的字符 $T[i + j]$ 与模式串对应字符 $p[j]$ 相同，则继续比较前一位字符。
      1. 如果模式串全部匹配完毕，则返回模式串 $p$ 在文本串中的开始位置 $i$。
   2. 如果文本串对应位置的字符 $T[i + j]$ 与模式串对应字符 $p[j]$ 不同，则：
      1. 根据后移位数表 $bc\underline{\hspace{0.5em}}table$ 和模式串末尾位置对应的文本串上的字符 $T[i + m - 1]$ ，计算出可移动距离 $bc\underline{\hspace{0.5em}}table[T[i + m - 1]]$，然后将模式串进行后移。
4. 如果移动到末尾也没有找到匹配情况，则返回 $-1$。

3. Horspool 算法代码实现

3.1 后移位数表代码实现

生成后移位数表的代码实现比较简单，跟 Boyer Moore 算法中生成坏字符位置表的代码差不多。具体步骤如下：

• 使用一个哈希表 $bc\underline{\hspace{0.5em}}table$， $bc\underline{\hspace{0.5em}}table[bad\underline{\hspace{0.5em}}char]$ 表示表示遇到坏字符可以向右移动的距离。
• 遍历模式串，以当前字符 $p[i]$ 为键，可以向右移动的距离（$m - 1 - i$）为值存入字典中。如果出现重复字符，则新的位置下标值会将之前存放的值覆盖掉。这样哈希表中存放的就是该字符在模式串中出现最右侧位置上的可向右移动的距离。

如果在 Horspool 算法的匹配过程中，如果 $T[i + m - 1]$ 不在 $bc\underline{\hspace{0.5em}}table$ 中时，可令其为 $m$，表示可以将模式串整个右移。如果 $T[i + m - 1]$ 在 $bc\underline{\hspace{0.5em}}table$ 中时，可移动距离就是 $bc\underline{\hspace{0.5em}}table[T[i + m - 1]]$ 。这样就能计算出可以向右移动的位数了。

生成后移位数表的代码如下：

# 生成后移位数表
# bc_table[bad_char] 表示遇到坏字符可以向右移动的距离
def generateBadCharTable(p: str):
    m = len(p)
    bc_table = dict()
    
    for i in range(m - 1):                      # 迭代到 m - 2
        bc_table[p[i]] = m - 1 - i              # 更新遇到坏字符可向右移动的距离
    return bc_table

3.2 Horspool 算法整体代码实现

# horspool 算法，T 为文本串，p 为模式串
def horspool(T: str, p: str) -> int:
    n, m = len(T), len(p)
    
    bc_table = generateBadCharTable(p)          # 生成后移位数表
    
    i = 0
    while i <= n - m:
        j = m - 1
        while j > -1 and T[i + j] == p[j]:      # 进行后缀匹配，跳出循环说明出现坏字符
            j -= 1
        if j < 0:
            return i                            # 匹配完成，返回模式串 p 在文本串 T 中的位置
        i += bc_table.get(T[i + m - 1], m)      # 通过后移位数表，向右进行进行快速移动
    return -1                                   # 匹配失败

# 生成后移位数表
# bc_table[bad_char] 表示遇到坏字符可以向右移动的距离
def generateBadCharTable(p: str):
    m = len(p)
    bc_table = dict()
    
    for i in range(m - 1):                      # 迭代到 m - 2
        bc_table[p[i]] = m - 1 - i              # 更新遇到坏字符可向右移动的距离
    return bc_table

print(horspool("abbcfdddbddcaddebc", "aaaaa"))
print(horspool("abbcfdddbddcaddebc", "bcf"))

4. Horspool 算法分析

• Horspool 算法在平均情况下的时间复杂度为 $O(n)$，但是在最坏情况下时间复杂度会退化为 $O(n * m)$。

参考资料

• 【书籍】柔性字符串匹配 - 中科院计算所网络信息安全研究组 译
• 【博文】字符串模式匹配算法：BM、Horspool、Sunday、KMP、KR、AC算法 - schips - 博客园