-
Notifications
You must be signed in to change notification settings - Fork 7
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
improve \adjustlimits #23
Comments
|
I think you could have a look at https://tex.stackexchange.com/a/409671/4427, with a modification I now realize is necessary, namely to add The original version hadn't With I get |
you need to read the TeXbook for that. TeX has some optimizations build in when it comes to use of registers. and that means it can be used as a "dimen" or as a number meaning 0 or 0pt depending on the circumstances. So it is not "usually" that it is "always" that. Box registers are really internally numbers as well so |
|
@FrankMittelbach: Thank you for the explanation, I did not know, that @eg9: You may also want to put a The actual problem with the current implementation is that it does not check the height of the limits. Based on https://tex.stackexchange.com/a/409671 and https://tex.stackexchange.com/a/410052 I made a variant which checks for the smallest needed distance (see last examples in the following). Including something like this would easily allow for a fix of Here is my variant \documentclass[margin=2mm]{standalone}
\usepackage{mathtools}
\usepackage{xparse}
\ExplSyntaxOn
\msg_new:nnnn {multiadjustlimits} {only_lower_limits} {
You~should~only~use~multiadjustlimits~with~lower~limits.
} {}
\NewDocumentCommand{\multiadjustlimits}{m}{
\group_begin:
\multiadjustlimits_measure:n { #1 }
\multiadjustlimits_print:n { #1 }
\group_end:
}
% We will later find the operator/limit pair with the largest sum of
% operator depth and limit height. These vales will be stored here.
\dim_new:N \l__multiadjustlimits_operator_depth_dim
\dim_new:N \l__multiadjustlimits_limit_height_dim
\cs_new_protected:Nn \multiadjustlimits_measure:n
{
\__multiadjustlimits_measure_recursion:nnn #1
\q_recursion_tail \q_recursion_tail \q_recursion_tail \q_recursion_stop
}
% Function to determine the largest sum of operator depth and limit
% height recursively.
\cs_new_protected:Nn \__multiadjustlimits_measure_recursion:nnn {
\quark_if_recursion_tail_stop:n {#1}
\quark_if_recursion_tail_stop:n {#2}
\quark_if_recursion_tail_stop:n {#3}
% Store operator and limit in a box
\hbox_set:Nn \l_tmpa_box { $\displaystyle#1$ }
\hbox_set:Nn \l_tmpb_box { $\scriptstyle\cramped{#3}$ }
% Check if the operator depths and limit height sum is larger than
% the currently stored one and overwrite in that case
\dim_compare:nNnTF {\box_dp:N \l_tmpa_box + \box_ht:N \l_tmpb_box}>{
\dim_use:N \l__multiadjustlimits_operator_depth_dim + \dim_use:N \l__multiadjustlimits_limit_height_dim
}{
\dim_set:Nn \l__multiadjustlimits_operator_depth_dim {
\box_dp:N \l_tmpa_box}
\dim_set:Nn \l__multiadjustlimits_limit_height_dim {
\box_ht:N \l_tmpb_box}
} {}
% Throw a warning if someone uses \multiadjustlimits with upper limits
\str_if_eq:nnTF {#2} {_} {} {
\msg_warning:nn {multiadjustlimits} {only_lower_limits}
}
% Recursion
\__multiadjustlimits_measure_recursion:nnn
}
\cs_new_protected:Nn \multiadjustlimits_print:n {
\__multiadjustlimits_print_recursion:nnn #1
\q_recursion_tail \q_recursion_tail \q_recursion_tail \q_recursion_stop
}
% Function to print the operators/limits recursively
\cs_new_protected:Nn \__multiadjustlimits_print_recursion:nnn {
\quark_if_recursion_tail_stop:n {#1}
\quark_if_recursion_tail_stop_do:nn {#2}{#1}
\quark_if_recursion_tail_stop_do:nn {#3}{#1#2}
\__multiadjustlimits_print:NNn {#1}{#2}{#3}
% Recursion
\__multiadjustlimits_print_recursion:nnn
}
% Function to print one operator with its limit
\cs_new_protected:Nn \__multiadjustlimits_print:NNn {
% Create a box for the operator and adjust the depth
\hbox_set:Nn \l_tmpa_box {$\displaystyle {#1}$}
\box_set_dp:Nn \l_tmpa_box {
\dim_use:N \l__multiadjustlimits_operator_depth_dim
}
% Create a box for the limit and adjust the height
\hbox_set:Nn \l_tmpb_box {$\scriptstyle\cramped{#3}$}
\box_set_ht:Nn \l_tmpb_box {
\dim_use:N \l__multiadjustlimits_limit_height_dim
}
% Print the operator/limit
\mathop { \mathopen{} \box_use:N \l_tmpa_box }
\limits
#2{ {}\box_use:N \l_tmpb_box }
}
\ExplSyntaxOff
\begin{document}
$\begin{aligned}
% It works in all cases where \adjustlimits works (examples from the documentation)
% &\adjustlimits\lim_{n\to\infty} \max_{p \leq n}
% & &\multiadjustlimits{\lim_{n\to\infty} \max_{p \leq n}}\\
% &\adjustlimits\lim_{n\to\infty} \max_{p^2 \leq n}
% & &\multiadjustlimits{\lim_{n\to\infty} \max_{p^2 \leq n}}\\
&\adjustlimits\lim_{n\to\infty} \sup_{p^2 \leq nK}
& &\multiadjustlimits{\lim_{n\to\infty} \sup_{p^2 \leq nK}}\\
&\adjustlimits\limsup_{n\to\infty} \max_{p \leq n}
& &\multiadjustlimits{\limsup_{n\to\infty} \max_{p \leq n}}\\
% And also in the cases, where \adjustlimits fails
&\adjustlimits\lim_{\tilde{N}\to\infty} \lim_{n\to\infty}
& &\multiadjustlimits{\lim_{\tilde{N}\to\infty} \lim_{n\to\infty}}\\
&\adjustlimits\lim_{n\to\infty} \lim_{\tilde{N}\to\infty}
& &\multiadjustlimits{\lim_{n\to\infty} \lim_{\tilde{N}\to\infty}}\\
\\
% Furthermore it also checks the smallest distance, compare
&&&\multiadjustlimits{\sup_{n<a} \max_{p^2\leq \tilde{N}}}\\
% and
&&&\multiadjustlimits{\max_{n<a} \sup_{p^2\leq \tilde{N}}}
\\
% It also allows for multiple operators
&&&\multiadjustlimits{\lim_{\tilde{N}\to\infty} \max_{n\leq\tilde{N}} \sup_{p^2\leq nK}}
\end{aligned}$
\end{document}And the output (left is the usual |
|
Am 14.03.21 um 16:46 schrieb torik42:
@FrankMittelbach <https://github.com/FrankMittelbach>: Thank you for the
explanation, I did not know, that |\z@| is only a register for the box.
no, \z@ is not a box register it is just away to write the number 0. The
box registers (as all TeX registers) are all accessible by number, e.g.
\box 0 \box 1 ...
If you say \newbox\foo then \foo is simply associated with the next free
number so \box\foo is the same as \box 123 (if that happens to be the
number allocated)
So \box\z@ is the same as saying \box 0 only slightly more efficient.
|
|
Thank you for explaining again @FrankMittelbach. This is how I also understood your last comment. I should have written something like “number for the register of the box”. @daleif: I think in the discussion above, which was very helpful for me, the actual issue got lost. The problem is that An easy fix which only sometimes produces a too large spacing is to always have the other operator/limit as a vertical phantom, i.e. something like \newcommand{\adjustlimits}[6]{%
\mathop{\vphantom{#4}\mathopen{}#1}\limits#2{\cramped{#3\vphantom{\cramped{#6}}}}
\mathop{\vphantom{#1}\mathopen{}#4}\limits#5{\cramped{#6\vphantom{\cramped{#3}}}}
}which is similar to the solution you suggested here but only for two limits. |






Initially I wanted to have the ability to also use
\adjustlimitsfor three (or even more) consecutive limits. For that reason I looked into the definition, but I am just learning LaTeX programming. While trying to understand the code, I think there are some mistakes.First thing I noticed is that
\adjustlimitsseems to be intended only for lower limits. However, I don’t currently need it for upper limits.For the other things, here is an example with a possible alternative definition. See the comments in the source.
And the output:
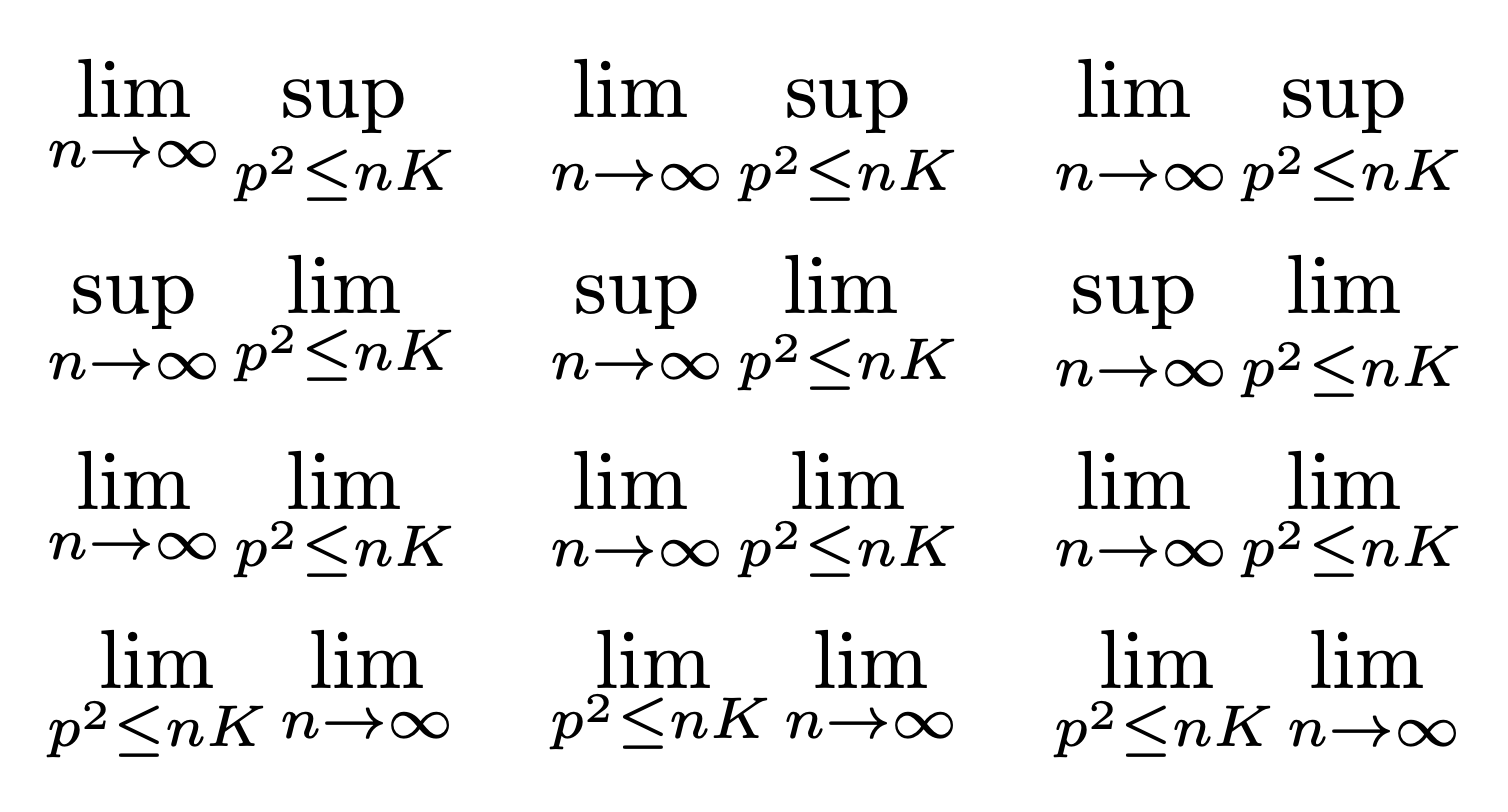
As noted in the source, I don’t exactly know what
\finsm@shand\mathsm@shdo, it is just copied from the source (\finsm@shis used by\mathsm@sh).The above definition is also easily extendable, for example the same for three operators would look like
I am quite sure that someone with more knowledge can expand this to work for any number of operators. Maybe one could add an optional argument to
\adjustlimitsto specify the number of operators that should be taken care of.PS: Independent of that, could someone explain to me the use of
\z@in the default definition? To my knowledge it is usually defined to be0pt. Then, in the default definition it is defined to be a box\sbox\z@{$\m@th \displaystyle #1$}(line 5183) which is used to calculate the difference of the depths of both boxes. Later it is used in\MH_if_dim:w \@tempdima>\z@(line 5196) to compare dimensions again, where I think it should be0ptagain. How is that possible? And what is it expected to be in\def\finsm@sh{\ht\z@\z@ \box\z@}(line 5201)?The text was updated successfully, but these errors were encountered: