Skip to content

Latest commit

 

History

History
326 lines (275 loc) · 17.4 KB

06Advanced_Plotting.md

File metadata and controls

326 lines (275 loc) · 17.4 KB
Raw

@[TOC](matlab绘图-进阶

进阶2D绘图


scatter()散点图

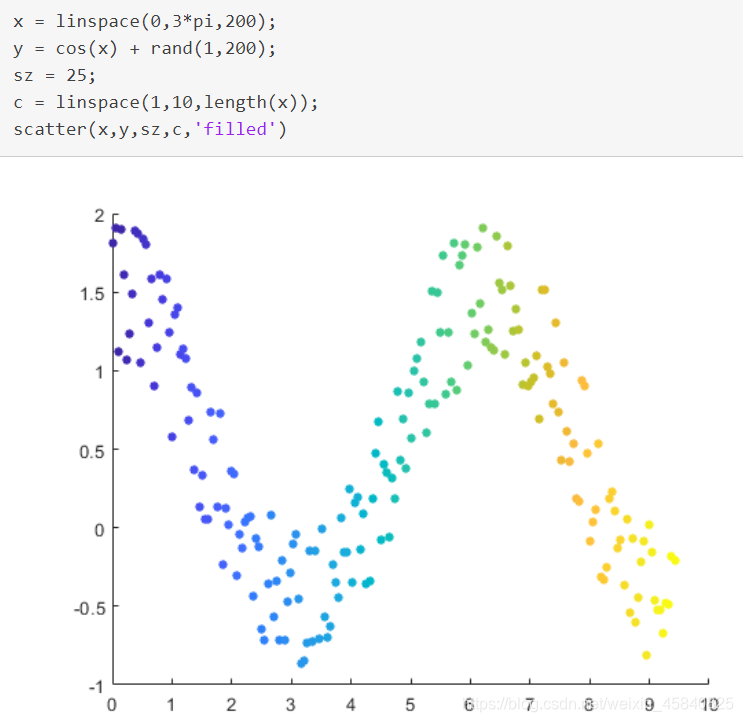
scatter(x,y) 在向量 x 和 y 指定的位置创建一个包含圆形的散点图。该类型的图形也称为气泡图。

scatter(x,y,sz) 指定圆大小。要绘制大小相等的圆圈，请将 sz 指定为标量。要绘制大小不等的圆，请将 sz 指定为长度等于 x 和 y 的长度的向量。 scatter(x,y,sz,c) 指定圆颜色。要以相同的颜色绘制所有圆圈，请将 c 指定为颜色名称或 RGB 三元组。要使用不同的颜色，请将 c 指定为向量或由 RGB 三元组组成的三列矩阵。 scatter(___,'filled') 填充圆形。可以将 'filled' 选项与前面语法中的任何输入参数组合一起使用。

scatter3() 绘制三维散点图。


loglog()对数图

semilogx(x,y)：x轴为对数画图； semilogy(x,y)：y轴为对数画图； loglog(x,y)：x、y轴为对数画图； set(gca,'XGrid','on')：在x轴上加上网格

yyaxis()一图双y轴

plotyy()

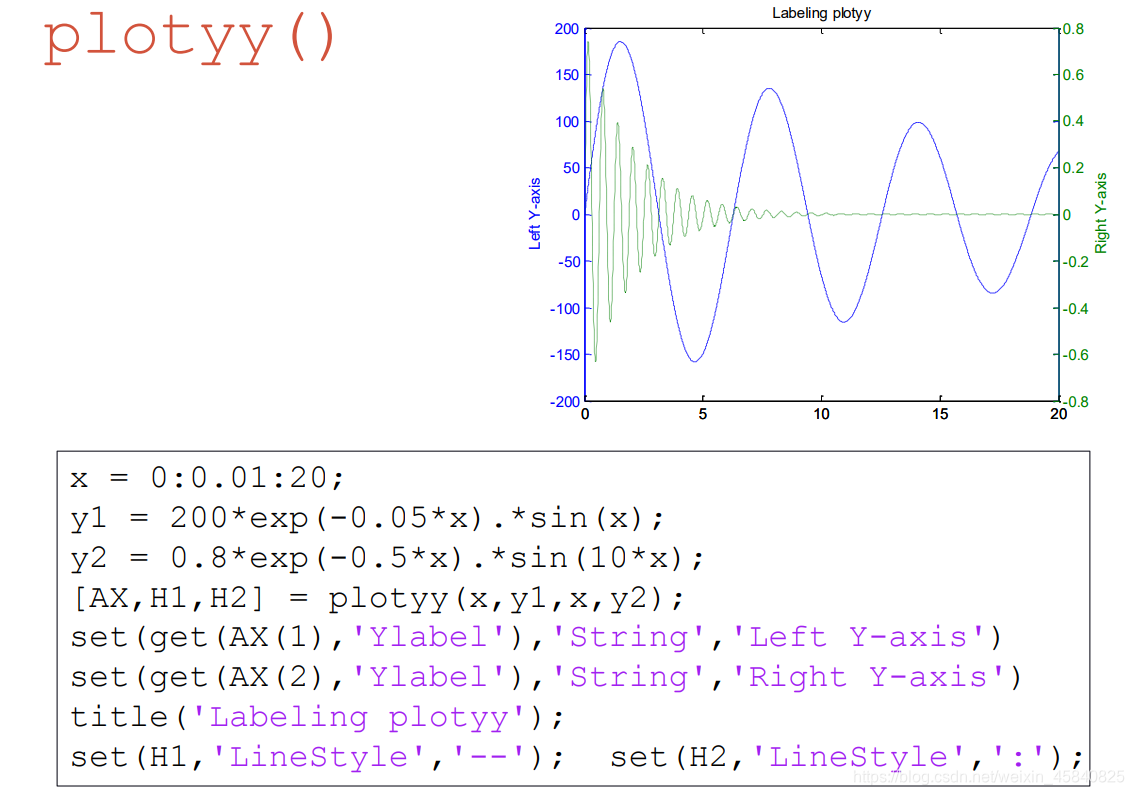
plotyy(X1,Y1,X2,Y2)：绘制 Y1 对 X1 的图，在左侧显示 y 轴标签，并同时绘制 Y2 对 X2 的图，在右侧显示 y 轴标签。 [AX,H1,H2] = plotyy( )：返回给AX两个坐标区(Axes)的句柄(handle)，AX(1)表示左边的坐标区的handle，AX(2) 表示右边的坐标区。返回给 H1 和 H2 每个绘图中Line对象的handle.

yyaxis()

相较于plotyy( )，新版本的matlab(R2016a起)更推荐yyaxis( )： yyaxis left 激活当前坐标区中与左侧 y 轴关联的一侧。后续图形命令的目标为左侧。 yyaxis right 激活当前坐标区中与右侧 y 轴关联的一侧。后续图形命令的目标为右侧。

clear all;
close all;
x=0:0.01:20;
y1=200*exp(-0.05*x).*sin(x);
y2=0.8*exp(-0.5*x).*sin(10*x);

yyaxis left;        %激活左侧
p1=plot(x,y1);
ylabel('Left Y-axis');
title('Labeling yyaxis');
p1.LineStyle='--';

yyaxis right;       %激活右侧
p2=plot(x,y2);
ylabel('Right Y-axis');
p2.LineStyle=':';

如上图所示，执行yyaxis left/right命令后，所有对图像的操作与初阶绘图时基本一致。

一些补充：

  • 若要对左边一侧画多条曲线，使用 hold on 命令。 hold on同时影响左右两侧，若右侧不需要画多条，请及时hold off.

  • 激活左侧，并==使用cla 命令来清除左侧曲线==：

yyaxis left;
cla；

hist()直方图

较新版本推荐使用 histogram() 代替原来的 hist()；

官方文档未明确指出从哪一版开始支持histogram()，我使用的是R2019b，亲测可以。

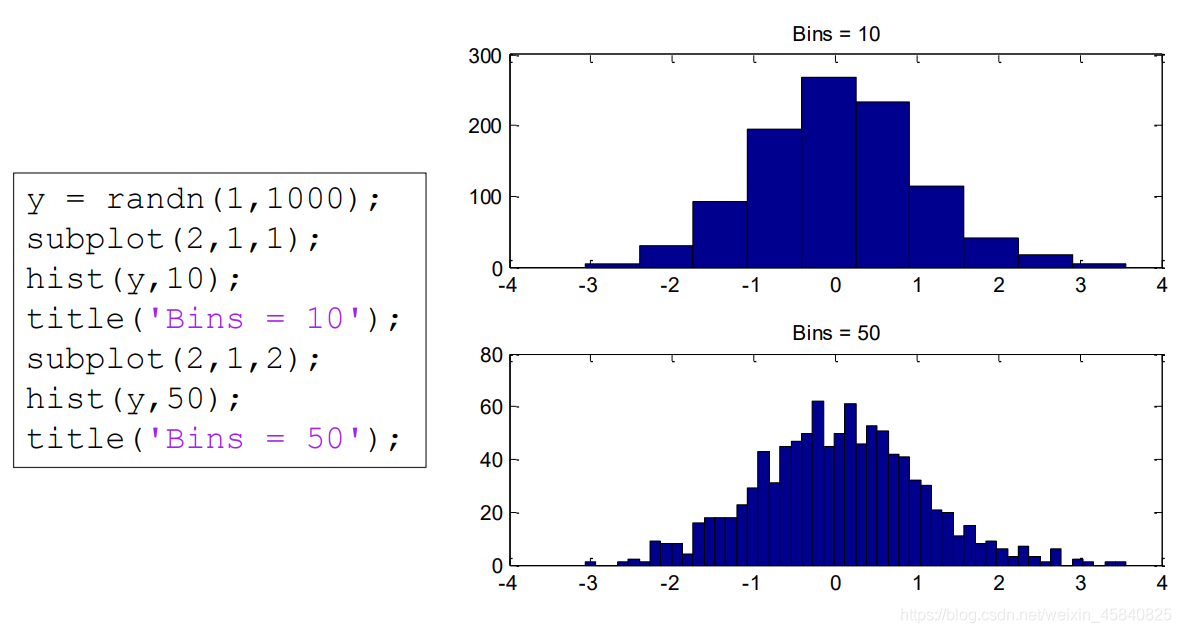
histogram(y) 基于 y 创建直方图。histogram 函数自动划分 bin. histogram(y,nbins) 使用标量 nbins 指定 bin 的数量.

bar()条形图

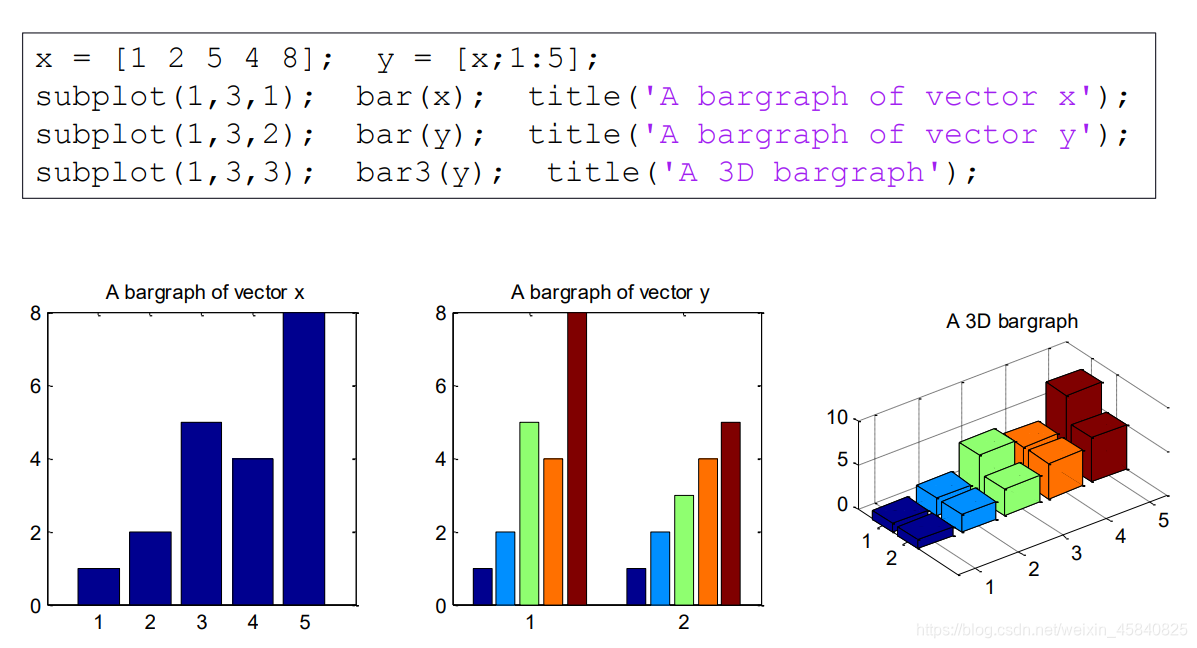
bar(y)：创建一个条形图

  • 如果 y 是向量，则y 中的每个元素对应一个条形，图中第1例；
  • 如果 y 是矩阵，则 bar 根据 y 中的行对条形分组，图中第2例

bar3( )：对应画3D图。 bar(x,y)：在 x 指定的位置绘制条形，x为数值向量

  • 若y为一个向量则长度必须与x相等，一个y值的条形对应于一个x；
  • 若y为一个矩阵，则行数必须与x长度相等，每一行的数据画为一组，每一组对应于一个x；当矩阵y的行数于列数均等于x长度时，x为组号。
  • 也可以使用字符串标注在x轴上，默认按字母顺序显示：
c = categorical({'apples','pears','oranges'});
bar(c,y)

bar(___,width)：设置条形的相对宽度以控制组中各个条形的间隔。 例如bar(y, 0.4)将所有条形的宽度设置为各条形可用总空间的 40%.

bar(___,color)：设置所有条形的颜色。 例如bar(y, 'r')将所有条形设置为红色。 bar(y,'stacked')：如图所示，显示为堆叠条形图。为矩阵中的每一行显示一个条形。每个条形的高度是行中各元素之和

barh() 水平绘制条形图，上文提及的所有对bar()的操作均可直接用于barh()；使用方式一致，将bar()换为barh()即可(bar3()换为bar3h())，效果为原来垂直显示变为水平显示。

pie()饼状图

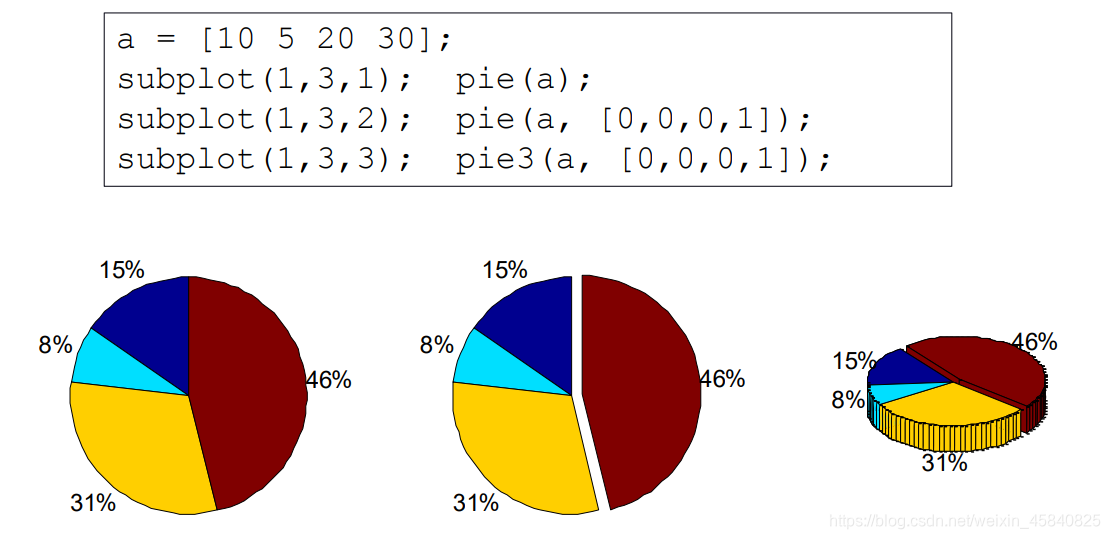
pie(a) 使用 a 中的数据绘制饼图。饼图的每个扇区代表 a 中的一个元素。

  • 若 sum(a) ≥ 0，则按比例绘制饼图；
  • 若 sum(a) < 1，则仅按比例绘制部分饼图

使用pie(a,explode)并将对应的 explode 元素设置为 1 来偏移对应扇区。如图中第2、3例。

使用pie(x,{'Taxes','Expenses','Profit'})来给对应扇区指定文本标签。注意所有文本用{}括起来，而不是[]。

pie3(a)：绘制三维饼状图。

polar()极坐标图

x = 1:100; theta = x/10; r = log10(x);
subplot(1,4,1); polar(theta,r);

theta = linspace(0, 2*pi); r = cos(4*theta); 
subplot(1,4,2); polar(theta, r);

theta = linspace(0, 2*pi, 6); r = ones(1,length(theta));
subplot(1,4,3); polar(theta,r);

theta = linspace(0, 2*pi); r = 1-sin(theta);
subplot(1,4,4); polar(theta , r);

polar(theta,r)：绘制极坐标图。 与plot(x,y)类似，描出所有点之后连线。只不过polar()中的参数对应于极坐标中的极角θ和极径r。

stairs()阶梯图与stem()取样图

stairs(y)/stairs(x,y)：与 plot(y)/plot(x,y) 原理一样，适用于plot()的属性 如指定线条颜色、粗细等，一般也可以直接用于stairs() 。 不同点在于，如上图所示，stairs() 通过平行于x,y轴的线段将所有点连结起来，而不是直接相连。

stem(y)/stem(x,y) 原理上也与plot()类似，但stem()不连结所描出的各点，而是将各点与x轴垂直相连。该函数适用于对曲线上某些特殊点取样。

fill()填充图

fill(x,y,ColorSpec) 填充 x 和 y 指定的二维多边形（颜色由 ColorSpec 指定） 比如上图 fill(x,y,'r') 画出多边形，并以红色填充。

axis square off命令实际上是初阶绘图中提及的axis square(使当前区域为正方形)和axis off(使数轴不可见)两个命令的组合命令。

text()函数在初阶绘图中已有简单介绍，下面是text()函数的部分参数说明：

  • 'Color'-文本颜色(具体颜色与代表符号 初阶绘图中有详细对比)；
  • 'FontSize'-字体大小；
  • ‘FontWeight'-字体粗细，指定为normal(默认)(正常)或bold(加粗)；
  • 'HorizontalAlignment'-相对于指定位置点 水平对齐文本。效果如下：


# 配色

RGB

[R G B]：一种颜色标准，通过对红(R)、绿(G)、蓝(B)三个颜色相互之间的叠加来得到各式各样的颜色。 通常使用0~255(十进制)之间的数来表示各成分占比。上图中右边的颜色对照板，则为对应颜色的十六进制表示。比如白色 [255 255 255] 十六进制为 [FF FF FF]，记作 #FFFFFF

数据可视化为图像

前面四行画出图中第一个立体图形，第五行的imagesc(z)命令将数据可视化为图像，而后对图像做一些修正。

使用colorbar指令调出如图所示的颜色条； 使用colormap()来改变可视化图像的颜色； colormap()的参数可以是以下这些： 这些参数实际上都是一个256x3的矩阵，每一行都对应一种颜色的[R G B]; 因此我们也可以人为地自定义一个表示颜色的矩阵来作为colormap()的参数。

三维绘图


plot3()三维线图

plot3(X,Y,Z) 描点连线，绘制三维点或线图。

  • 要绘制一条线图，请将 X、Y、Z 指定为相同长度的向量。
  • 要在同一组坐标轴上绘制多条线图，请将 X、Y 或 Z 中的至少一个指定为矩阵，其他指定为向量。

原理上于plot()一致，在使用上，各参数也基本与 plot() 对应相同。

surf()三维网图

[X,Y]=meshgrid(x,y)：基于向量 x 和 y 中包含的坐标返回二维网格坐标。也就是说前面给出的x、y只是一个向量，而画网图需要x、y两个范围围出来的面上的所有点，meshgrid(x,y)则给出这个面上所有的点。 mesh()：绘制网格图； surf()：绘制网格图并为网格填充颜色。

事实上，从R2016b开始，并不总是需要先用meshgrid()创建网格然后才能绘制图像；比如该例，直接使用 surf(x,y,x.*exp(-x.^2-(y').^2)) 也能得到以上效果。



习题

close all;
clear all;
x=[1 2 5 4 8];
y=[x;1:5];
subplot(1,2,1);
bar(y,'stacked');   %绘制竖直堆叠图
title('竖直堆叠图');

subplot(1,2,2);     %绘制水平堆叠图
barh(y,'stacked');
title('水平堆叠图');

效果如下： 

clear all;
close all;
a = [10 5 20 30];
pie(a,[1 1 1 1]);	%分开所有扇区

clear all;
close all;
theta = linspace(0, 2*pi, 7);   %把2π划分为6块
r = ones(1,length(theta));
polar(theta,r);                 %画一个六边形


clear all;
close all;
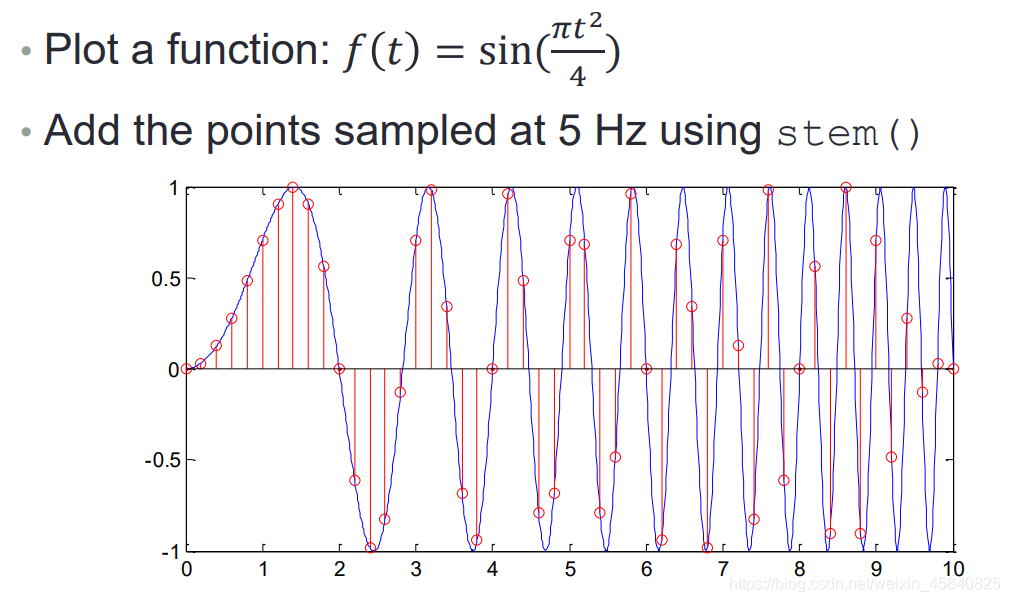
t=linspace(0,10,1000);
f=sin(pi*(t.^2)/4);
plot(t,f);      %第一步，画出蓝色的曲线
hold on;

x=linspace(0,10,50);
y=sin(pi*(x.^2)/4);
stem(x,y);      %第二步，1秒取五次样


close all;
clear all;
t=(0:4)*pi/2;
x=sin(t);y=cos(t);
h=fill(x,y,'y');        %绘制一个以黄色填充的多边形
h.LineWidth=5;          %将填充多边形的边界曲线设置粗度
axis square off;        %把显示区域变为正方形，并隐藏数轴

% 在填充的多边形中加上'WAIT'字样
text(0,0,'WAIT','color','k','FontSize',65, ...
    'FontWeight','bold','HorizontalAlignment','center');

对于这道题，在绘制填充多边形时，我使用了h=fill()，从而获得边界曲线的handle，进而在下一步设置边界曲线的粗度。


要指定条形图某些条形的颜色，可以使用 Bar 对象的 CData 属性来控制单个条形的颜色。 在这之前，需要先将 Bar 对象的 FaceColor 属性设置为 'flat'；可以在画图时直接设置bar(....,'FaceColor','flat')，或者后期单独指定b.FaceColor = 'flat'。

G = [46 38 29 24 13]; 
S = [29 27 17 26 8];
B = [29 23 19 32 7]; 
% 指定字符串标记x轴
str=categorical({'USA','CHN','GBR','RUS','KOR'}); 
% 画图的同时将各条形的handle赋给h，并将FaceColor属性设置为flat
h = bar(str, [G' S' B'],'FaceColor','flat');

for i=1:size(G',1)      % 将每组第一个条形设置为金色
    h(1).CData(i,:)=[1,0.843,0];        
end
for i=1:size(G',1)      % 将每组第二个条形设置为银色
    h(2).CData(i,:)=[0.753 0.753 0.753];
end
for i=1:size(G',1)      % 将每组第三个条形设置为铜色
    h(3).CData(i,:)=[.545,.27,.0745];
end
title('Medal count for top 5 countries in 2012 Olympics');
ylabel('Number of medals'); xlabel('Country');
legend('Gold', 'Silver', 'Bronze')  % 加上图例

该例中几个需要注意的点：

  1. G、S、B三个向量需要先转置再串联起来，因为bar()是将矩阵的每一行分为一组，分别画出条形；
  2. 将条形的handle赋给h时，实际上是G、S、B三个列的handle，h是一个1x3的bar数组，因此使用时分别对h(1),h(2),h(3)进行操作；
  3. 在进行颜色设置时，matlab似乎不支持使用0~255的数组来表示[R G B],将0~255的数组每一项均除以255转换为0~1来表示即可。

x = [1:10; 3:12; 5:14];
imagesc(x);
colorbar;
map = zeros(256,3);
map(:,2) = (0:255)/255;	%除以255，转换为0~1表示
colormap(map);



以上内容为个人笔记，部分图片来源于郭老师课件或课程截图。 笔记汇总：MATLAB基础教程 课程视频：https://www.bilibili.com/video/BV1DA411Y7bN 课件下载：MATLAB教程 郭彦甫老师的YouTube主页：@Yanfu Kuo 原视频：https://www.youtube.com/watch?v=KHFZLkm9qs0&t=8s