notes from 2022-02-01 meeting with Khachik

[ghost]

notes

sparse quadrature

can different sampling methods per-variable improve the accuracy / efficiency of the surrogate?

• sparse quadrature
  • build with projection instead of regression
  • “quadrature usually doesn’t work for physical models because of noise or whatever”

here's an example of a sparse sampling method that the authors call "Smolyak sparse grid from the extrema of Chebyshev polynomials (Clenshaw-Curtis quadrature)"

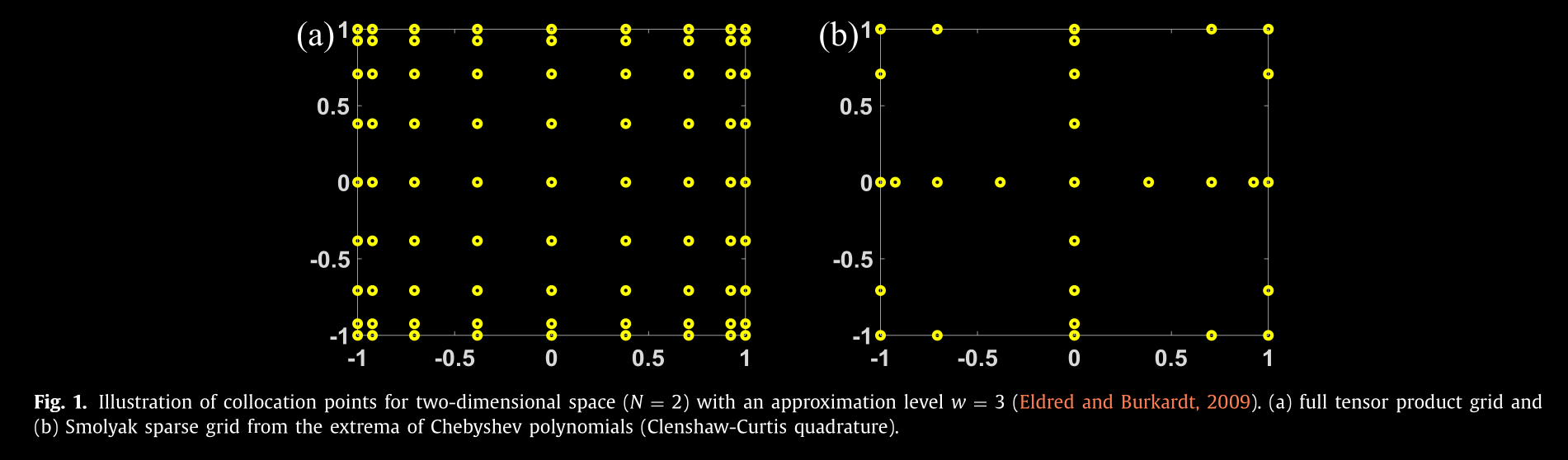
from https://www.sciencedirect.com/science/article/pii/S0098135419310026

methods and constraints

method	regularization	penalty parameter?
Bayesian Compressed Sensing	L1	✔️
Lasso-Type Regularization	L1	✔️
Bayesian Ridge	L2	✔️

regularization	constraint
L1	sparsity
L2	smoothness

• UQTk uses “Bayesian compressed sensing”
• the “penalty parameter” needs to be played around with to get good results

polynomial order / count determination

the number of expanded polynomials M can be found by

M + 1 = (N + P)! / (N! * P!)

where N is the number of variables and P is the highest order.

This is equation 5 from https://www.sciencedirect.com/science/article/pii/S0098135419310026:

Therefore, a 3rd order polynomial with 4 variables expands to 34 polynomials (plus a zeroth order polynomial)

as a rule of thumb, with an L2 constraint the number of data points D should be approx

D ~= 10 * M

However, Lasso-Type Regularization and Bayesian Compressed Sensing can both fit against a large fraction of polynomials vs data points less than 10 * M

mesh perturbation

• mesh size is a “hyperparameter”
  • numerical and not physical
  • Khachik is unsure if we can use this methodology to get sensitivity

next steps

• look into the possibility of building a sparse quadrature #73
• attempt to plot comparison plot with color values along some spatial axis
  • perhaps along the northeast line, or distance from the storm centerline?
• see if the problem with negative polynomial values is a problem
  • solution 1: model logarithm of water elevation and attempt to build surrogate
  • solution 2: model water depth instead of water elevation
• build an ensemble with a number of data points (ensemble members) greater than or equal to the number of polynomials #72