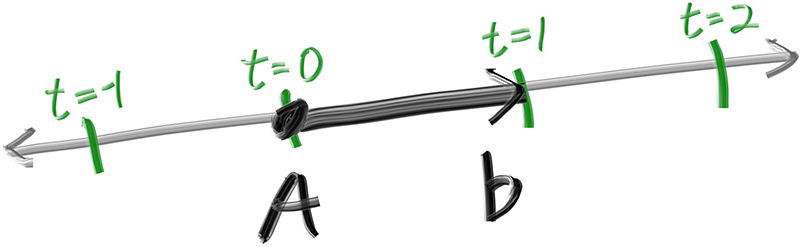Skip to content

Latest commit

 

History

History
154 lines (106 loc) · 7.84 KB

ch_4_Rays, a Simple Camera, and Background.md

File metadata and controls

154 lines (106 loc) · 7.84 KB
Raw

이 글은 Peter Shirley의 Ray Tracing in One Weekend를 번역한 것입니다. Ray Tracing in One Weekend를 공부하면서 다시 한번 복습하는 느낌으로 번역을 해보려고 합니다. 영어가 서툴러 번역이 잘못되었을 수도 있으므로 잘못된 부분을 발견하신다면 지적해 주시면 감사하겠습니다.

4.1 The ray Class

모든 레이 트레이서는 광선(ray)을 따라서 어떤 색이 보이는지 계산하는 ray 클래스를 가지고 있습니다. 광선을 함수 P(t) = A + tb라고 생각해봅시다. P는 3D 공간에서 한 직선상의 위치입니다. A는 광선의 원점이고 b는 광선의 방향입니다. 파라미터 t는 실수(real number)입니다(코드 상에서는 double형). 함수 P(t)에 t의 값을 변화시키며 대입하면 P(t)는 광선을 따라 이동합니다. 음수 t 값을 더하면 3D 직선의 어디든지 갈 수가 있습니다. 양수 t 값으로는 오직 A(광선의 원점)의 앞쪽(b방향)으로만 이동할 수 있으며 이것을 반직선(half-line) 또는 광선(ray)라고 합니다.

Figure 2: Linear interpolation

더 자세한 코드 상에서 함수 P(t)는 ray::at(t)라고 하겠습니다.

#ifndef RAY_H
#define RAY_H

#include "vec3.h"

class ray {
  public:
    ray() {}
    ray(const point3& origin, const vec3& direction)
      : orig(origin), dir(direction)
    {}

    point3 origin() const { return orig; }
    vec3 direction() const { return dir; }

    point3 at(double t) const {
      return orig + t * dir;
    }

  public:
    point3 orig;
    vec3 dir;
};

#endif

Listing 8: [ray.h] The ray class

4.2 Sending Rays Into the Scene

이제 한 고비 넘기고 레이 트레이서를 만들 준비가 되었습니다. 광선이 카메라 위치에서 스크린의 픽셀을 통과하도록 보내고 이 광선들의 방향에서 보이는 색을 계산하는 것이 레이 트레이서의 핵심입니다. 해당 단계들은 다음과 같습니다.

  1. 눈(카메라)에서 픽셀까지의 광선을 계산한다.
  2. 광선이 부딪치는 오브젝트들을 결정한다.
  3. 광선이 부딪친 위치의 색을 계산한다.

레이 트레이서를 처음 만들 경우, 저는 코드 실행을 위해서 항상 간단한 카메라를 사용합니다. 또한 배경 색(단순한 그라디언트)을 반환하는 간단한 ray_color(ray) 함수를 만듭니다.

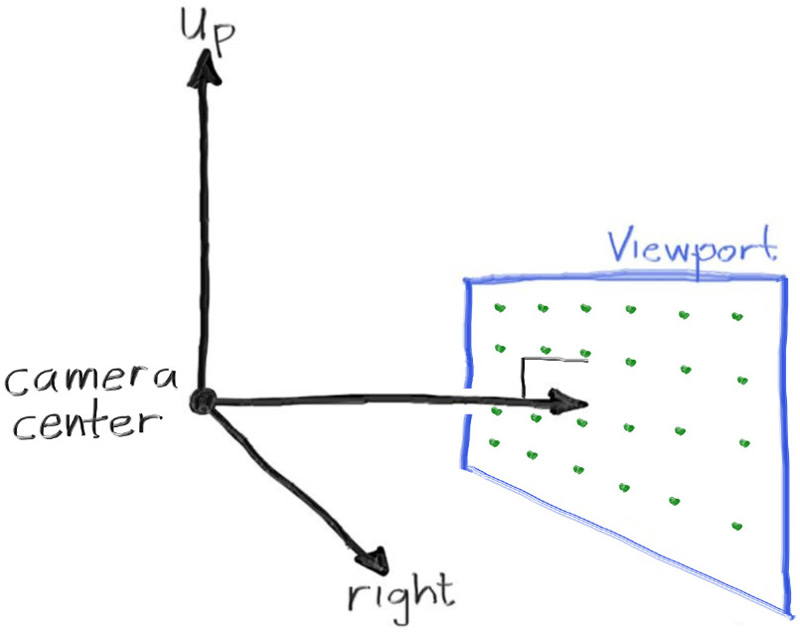
x 축 좌표와 y 축 좌표를 자주 바꾸는 경우, 정사각형 이미지를 디버깅하는 것은 어렵습니다. 그러므로 정사각형 이미지는 사용하지 않을 것입니다. 이제부터 아주 일반적인 16:9 비율 이미지를 사용하겠습니다. 렌더링 된 이미지의 픽셀 치수(pixel dimensions)를 설정하는 것 이외에 광선들을 통과하는 가상 뷰포트(view port)를 설정해야 합니다. 표준 정사각형 픽셀 간격의 뷰포트의 종횡비는 렌더링 된 이미지와 같아야 합니다. 높이가 단위 길이 2인 뷰포트를 사용하겠습니다. 투영 평면(projection plane)과 투영점(projection point) 사이의 거리는 단위 길이 1로 설정합니다. 이 값을 초점 길이(focal length)라고 합니다. 나중에 다룰 초점 거리(focus distance)와 혼동하지 마십시오.

❗projection plane은 view port를 projection point는 카메라(눈)이 위치하고 있는 원점을 의미하는 것 같습니다. ❗focal length와 focus distance는 어떻게 번역해야할지 몰라서 일단 각각 초점길이와 초점거리로 번역했습니다.

원점 (0, 0, 0)에 눈(또는 카메라)를 위치시킵니다. y 축 방향은 위를 향하고, x 축 방향은 오른쪽을 향합니다. 오른손 좌표계에서 z 축 방향은 스크린에서 밖으로 나오는 방향입니다. 스크린의 왼쪽 하단에서부터 순회를 할 것입니다. 그리고 스크린을 교차하는 광선의 끝점을 움직이기 위해 두 오프셋 벡터를 사용합니다. 광선 방향을 단위 벡터로 만들지 않을 것입니다. 단위 벡터로 만들지 않으면 코드가 더 간단해지고 약간 더 빨라지기 때문입니다.

Figure 3: Camera geometry

❗위 그림 상에서 뷰포트의 너비는 4이지만 아래 코드에서는 종횡비 x 뷰포트 높이 = 16.0 / 9.0 x 2 이므로 약 3.5555입니다.

아래의 코드에서 광선 r은 픽셀 중심을 근접하게 지나갑니다(나중에 안티엘리어싱(anti-aliasing)을 추가할 것이기 때문에 정확성은 걱정하지 않아도 됩니다.):

#include "color.h"
#include "ray.h"    // 추가
#include "vec3.h"

#include <iostream>

/* ************* 추가 ************ */
color ray_color(const ray& r) {
  vec3 unit_direction = unit_vector(r.direction());
  auto t = 0.5 * (unit_direction.y() + 1.0);
  return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}
/* ******************************* */

int main() {

  // Image
/* ************* 추가 ************ */
  const auto aspect_ratio = 16.0 / 9.0;
  const int image_width = 400;
  const int image_height = static_cast<int>(image_width / aspect_ratio);

  // Camera
  auto viewport_height = 2.0;
  auto viewport_width = aspect_ratio * viewport_height;
  auto focal_length = 1.0;

  auto origin = point3(0, 0, 0);
  auto horizontal = vec3(viewport_width, 0, 0);
  auto vertical = vec3(0, viewport_height, 0);
  auto lower_left_corner = origin - horizontal / 2 - vertical / 2
  			   - vec3(0, 0, focal_length);
/* ******************************* */

  // Render

  std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";

  for (int j = image_height - 1; j >= 0; --j) {
    std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
    for (int i = 0; i < image_width; ++i) {
/* ************* 추가 ************ */
      auto u = double(i) / (image_width - 1);
      auto v = double(j) / (image_height - 1);
      ray r(origin, lower_left_corner + u * horizontal + v * vertical
      		- origin);
      color pixel_color = ray_color(r);
/* ******************************* */
      write_color(std::cout, pixel_color);
    }
  }

  std::cerr << "\nDone.\n";
}

Listing 9: [main.cc] Rendering a blue-to-white gradient

ray_color(ray) 함수는 광선 방향을 단위 길이로 스케일링 한 후에 y 좌표의 높이에 따라 선형적으로 파란색과 흰색을 섞습니다(-1.0 < y < 1.0). 벡터를 정규화 한 후에 y 높이를 보기 때문에, 결과 이미지에서 수직 그라디언트뿐만 아니라 수평 그라디언트도 확인할 수 있습니다.

여기서는 0.0 <= t <= 1.0으로 스케일링하는 표준 그래픽스 트릭을 사용했습니다. t = 1.0일 때는 파란색, t = 0.0일 때는 흰색이 표현되어야 하고 그 사이 지점에서는 두 색을 혼합합니다. 이런 방법을 선형 블렌딩(linear blend), 선형 보간(linear interpolation), 짧게 "lerp"라고 합니다. lerp는 항상 t가 0부터 1까지 변화하는 다음의 형태를 따릅니다.

              blendedValue = (1 − t) ⋅ startValue + t ⋅ endValue

코드를 실행하면 다음과 같은 결과를 얻을 수 있습니다.

Image 2: A blue-to-white gradient depeding on ray Y coordinate

출처

Ray Tracing in One Weekend - Peter Shirley https://raytracing.github.io/books/RayTracingInOneWeekend.html#rays,asimplecamera,andbackground