The Boyer Moore Algorithm was established by Robert Boyer and J Strother Moore in 1977. The Boyer Moore (B-M) String search algorithm is a particularly efficient algorithm and has served as a standard benchmark for string search algorithm ever since.The algorithm takes a 'backward' approach: the pattern string (P) is aligned with the start of the text string (T), and then compares the characters of a pattern from right to left, beginning with rightmost character.If a character is compared that is not within the pattern, no match can be found by analyzing any further aspects at this position so the pattern can be changed entirely past the mismatching character.
The B-M algorithm ,for deciding the possible shifts, uses two preprocessing strategies simultaneously. Whenever a mismatch occurs, the algorithm calculates a variation using both approaches and selects the more significant shift thus, if make use of the most effective strategy for each case. The two strategies are called heuristics of B - M as they are used to reduce the search. They are:
- Bad Character Heuristics
- Good Suffix Heuristics
Bad Character Heuristic The idea of bad character heuristic is simple. The character of the text which doesn’t match with the current character of the pattern is called the Bad Character. Upon mismatch, we shift the pattern until –
- The mismatch becomes a match
- Pattern P move past the mismatched character.
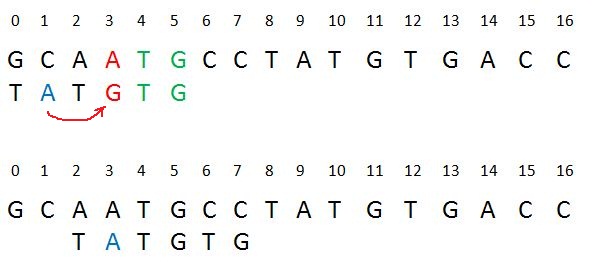
- Case 1 – Mismatch become match
We will lookup the position of last occurrence of mismatching character in pattern and if mismatching character exist in pattern then we’ll shift the pattern such that it get aligned to the mismatching character in text T.
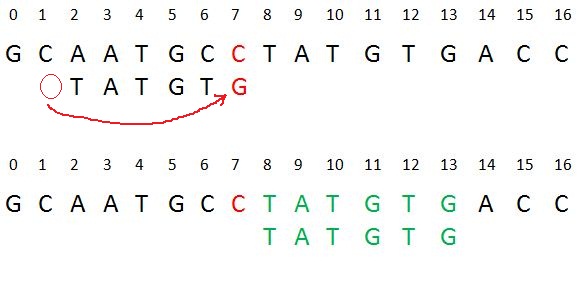
- Case 2 – Pattern move past the mismatch character
We’ll lookup the position of last occurrence of mismatching character in pattern and if character does not exist we will shift pattern past the mismatching character.
Good Suffix Heuristic
Let t be substring of text T which is matched with substring of pattern P. Now we shift pattern until :
- Another occurrence of t in P matched with t in T.
- A prefix of P, which matches with suffix of t
- P moves past t
- Case 1: Another occurrence of t in P matched with t in T
Pattern P might contain few more occurrences of t. In such case, we will try to shift the pattern to align that occurrence with t in text T. For example-
- Case 2: A prefix of P, which matches with suffix of t in T
It is not always likely that we will find the occurrence of t in P. Sometimes there is no occurrence at all, in such cases sometimes we can search for some suffix of t matching with some prefix of P and try to align them by shifting P. For example –
- Case 3: P moves past t
If the above two cases are not satisfied, we will shift the pattern past the t. For example –
fullSuffixMatch(shiftArray, borderArray, pattern)
Input: Array to store shift locations, the border array and the pattern to search
Output: Fill the shift array and the border array
Begin
n := pattern length
j := n
j := n + 1
borderArray[i] := j
while i > 0, do
while j <= n AND pattern[i - 1] ≠ pattern[j - 1], do
if shiftArray[j] = 0, then
shiftArray[j] := j - i;
j := borderArray[j];
done
decrease i and j by 1
borderArray[i] := j
done
End
partialSuffixMatch(shiftArray, borderArray, pattern)
Input: Array to store shift locations, the border array and the pattern to search
Output: Fill the shift array and the border array
Begin
n := pattern length
j := borderArray[0]
for index of all characters ‘i’ of pattern, do
if shiftArray[i] = 0, then
shiftArray[i] := j
if i = j then
j := borderArray[j]
done
End
searchPattern(text, pattern)
Input: The main text and the pattern, that will be searched
Output: The indexes where the pattern is found
Begin
patLen := pattern length
strLen := text size
for all entries of shiftArray, do
set all entries to 0
done
call fullSuffixMatch(shiftArray, borderArray, pattern)
call partialSuffixMatch(shiftArray, borderArray, pattern)
shift := 0
while shift <= (strLen - patLen), do
j := patLen -1
while j >= 0 and pattern[j] = text[shift + j], do
decrease j by 1
done
if j < 0, then
print the shift as, there is a match
shift := shift + shiftArray[0]
else
shift := shift + shiftArray[j + 1]
done
End
Input: txt[] = "THIS IS A TEST TEXT"
pat[] = "TEST"
Output: Pattern found at index 10
Input: txt[] = "AABAACAADAABAABA"
pat[] = "AABA"
Output: Pattern found at index 0
Pattern found at index 9
Pattern found at index 12
Preprocessing Time Complexity: O(|∑|)
Matching Time Complexity: (O ((n - m + 1) + |∑|))