-
Notifications
You must be signed in to change notification settings - Fork 4
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Large-scale dissipation vs. lateral entrainment question #10
Comments
|
@amrapallig @qingli411 Do you have any thoughts on this? I noticed that Qing's version of the code has removed the dissipation tendency equation so that it is always estimated using the TKE/length scale closure. |
|
So the u'2 and v'2 have been a tough one to think about for me. It is not clear those quantities are plume scale quantities to me. the MFC framework does not hold for momentum. Also at plume scale I would expect w'2 >> u'2 or v'2. I'm not sure we should cast dissipation as with the lateral entrainment detrainment terms. In my mind those should be a traditional HOC formulation. This is consistent with Lappen (1999) -- the dissertation where the 2001(a)-(c) papers stem from. However, you could then question if the model is energetically consistent. Perhaps plume scale KE should be something like w'2 / 2 instead of the summation. Regarding your second question, I think in Lappen and Randall (2001b) they argue the lateral entrainment/detrainment takes on the role of -2/3 epsilon. If that argument is to believed than think the model is consistent as is. So I'm not convinced eps_ls should be 1/6 or 1/2 of the entrainment/detrainment term Finally the dissipation tendency equation was a thought on how to get rid of the Bogeault closure which is not feasible for global ocean simulations given how expensive the buoyancy calculation will be with a nonlinear EOS. The TKE/length closure simply follows Cara-lynn's Dissertation. It is probably not the greatest idea given the source sink choices made in the model, unless we believe the lateral entrainment term takes on the role of -2/3 epsilon. If that is to be assumed though there seems no reason to use that formulation in the u2 and v2 budgets, even though those equations really aren't MFC applicable. I guess I need to think about this more. Thanks for raising the issue. |
@vanroekel I have two questions about the large-scale dissipation rate ($\epsilon_{ls}$ ) in the current ADC code:
epstend) or through a simple $\epsilon_{ls}\propto KE^{3/2}/L$ closure, rather than by coupling it to the lateral entrainment/detrainment term (which Lappen and Randall say represents the transfer of energy from plume-scale to sub-plume scale turbulence)?The Lappen & Randall 2001 papers are not very clear about how they define the large-scale dissipation rate ($\epsilon_{ls}$ ; equivalent to the rate of energy transfer/cascade from plume-scale to sub-plume-scale motions). This dissipation rate appears in the sub-plume scale TKE budgets in their second paper (calculated separately for upwelling and downwelling plumes):
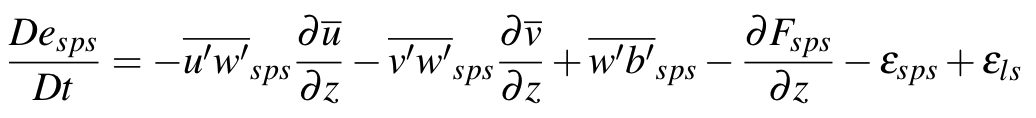
$\epsilon_{ls}$ should be equal to the entrainment/detrainment term in the w2 budget multiplied by 1/2 to convert to kinetic energy (or perhaps 1/6 if it is assumed to act equally on u2 and v2 as well). With $\epsilon_{ls}$ partitioned between upwelling and downwelling sub-plume TKE budgets as,
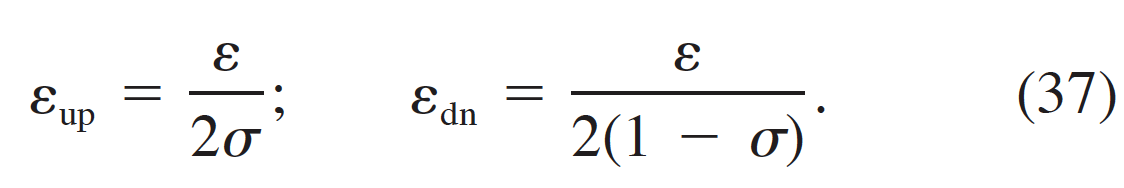
Despite not explicitly defining this dissipation rate, they discuss in the first paper that the entrainment/detrainment term represents the transfer of plume-scale TKE to sub-plume scale TKE. This suggests that
The text was updated successfully, but these errors were encountered: