Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1, and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).
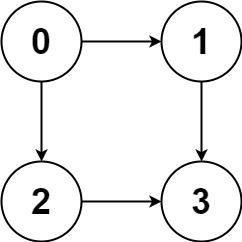
Example 1:
Input: graph = [[1,2],[3],[3],[]] Output: [[0,1,3],[0,2,3]] Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
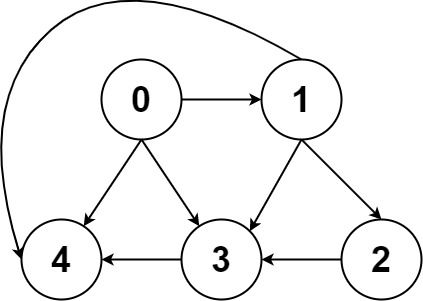
Example 2:
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]] Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Example 3:
Input: graph = [[1],[]] Output: [[0,1]]
Example 4:
Input: graph = [[1,2,3],[2],[3],[]] Output: [[0,1,2,3],[0,2,3],[0,3]]
Example 5:
Input: graph = [[1,3],[2],[3],[]] Output: [[0,1,2,3],[0,3]]
Constraints:
n == graph.length2 <= n <= 150 <= graph[i][j] < ngraph[i][j] != i(i.e., there will be no self-loops).- The input graph is guaranteed to be a DAG.