We read every piece of feedback, and take your input very seriously.
To see all available qualifiers, see our documentation.
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
通常在评价一个算法的时候,要做两项分析。第一是分析算法的正确性,如果一个算法没有通过正确性验证,那就是无意义的;第二是算法复杂度的分析,算法复杂度能很大程度上反应算法的优劣。
算法的复杂度又分为时间复杂度和空间复杂度。
时间复杂度是指执行算法所需要的计算工作量。 空间复杂度是指算法执行所需要的内存空间。
大多数的情况下,更多的是考虑时间复杂度。
在计算机科学中,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大 O 符号表述,不包括这个函数的低阶项和首项系数。
时间复杂度是以算法输入值规模 n 为自变量的函数:。
时间复杂度的表达方式一共有3种,分别为:
通常的情况下,我们用 O 来表达算法的时间复杂度
当我们得到一个算法时间复杂度的函数表达式时,需要对其常数项和次要项进行舍弃,以得到最终的时间复杂度表达式。
当我们得到下面这个时间复杂度的函数表达式时
我们需进行常数项和次要项的舍弃,最终结果为:
接下看一张图。
图中增长速度越快的表达式的级别越高,当算法时间复杂度的函数表达式同时拥有图中多种表达式时,只保留级别最高的表达式,其余的当做次要项舍弃。
例如:
在计算时间复杂度的时候,一般要考虑以下几点:
看几个例子:
function demo1(array) { let max = array[0]; for (let i = 1; i < array.length; i++) { if (max < array[i]) { max = array[i]; } } return max; }
从上面的代码可以知道,基本操作就是if操作,时间复杂度为1;当我们假设n = array.length时,基本操作被执行的次数就是n-1次,所以其时间复杂度为,去除常数项和次要项,算法时间复杂度为。
if
1
n = array.length
n-1
再来看看复合操作的例子。
function demo2(arrA, arrB) { for (let i = 0; i < arrA.length; i++) { console.log('[' + arrA[i] + ']'); } for (let j = 0; j < arrB.length; j++) { console.log('[' + arrB[j] + ']'); } } function demo3(arrA, arrB) { for (let i = 0; i < arrA.length; i++) { for (let j = 0; j < arrB.length; j++) { console.log('[' + arrA[i] + ',' + arrB[j] + ']'); } } }
demo2 中,先遍历 arrA,再遍历 arrB,所以其时间复杂度应该是相加的,为。而在 demo3 中,每进行一次 arrA 的取值,都要将 arrB 遍历一遍,所以其时间复杂度应该是相乘的,为。
arrA
arrB
来看一个 demo3 的变种:
function demo4(arr) { for (let i = 0; i < arr.length; i++) { for (let j = i; j < arr.length; j++) { console.log('[' + arr[i] + ',' + arr[j] + ']'); } } }
假设 arr.length = n,那么我们可以推导出,外侧for循环第一次执行时,内侧for循环里面的代码会被执行n次;外侧循环第二次自执行时,内侧循环的代码会被执行n-1次;依次类推,内侧循环代码会依次被执行n-2、n-3、……、2、1,这是一个等差数列,对其进行求和,得到算法时间复杂度的函数表达式为,经过去除常数项和次要项,最终得到时间复杂度为。
arr.length = n
for
n
n-2、n-3、……、2、1
什么是递归?
递归,又译为递回,在数学与计算机科学中,是指在函数的定义中使用函数自身的方法。递归一词还较常用于描述以自相似方法重复事物的过程。例如,当两面镜子相互之间近似平行时,镜中嵌套的图像是以无限递归的形式出现的。也可以理解为自我复制的过程。
比如说阶乘就可以用递归来求,看代码。
function demo4(n) { if (n === 1) { return 1; } else { return n * demo4(n - 1); } }
当我们求n的阶乘时,demo(n) = n * demo(n-1),需要先求n-1的阶乘。推导下去,需要依次计算(n-1)、(n-2)、……、2、1阶乘,且每次只做一次乘法运算,最后一次直接赋值,所以需要做n次运算,所以时间复杂度为 。
demo(n) = n * demo(n-1)
(n-1)、(n-2)、……、2、1
再看一个代码。
function demo5(n) { if (n === 1) { return 1; } else { return demo5(n - 1) * demo5(n - 1); } }
当要计算demo5(n)时,就需要先去计算demo5(n-1) + demo5(n-1);依次类推,最后需要计算个demo5(1)。将所有需要计算的项用下图来表示:
demo5(n)
demo5(n-1) + demo5(n-1)
demo5(1)
那么需要进行计算的次数为1、2、4、……、2^(n-1),为一个等比数列,每次基本操作计算的时间复杂度为1,那么整个时间复杂度的函数表达式为,经过计算之后去除常数项和次要项,最终时间复杂度为。
1、2、4、……、2^(n-1)
结论
对于递归问题的时间复杂度,有一个经验性结论:递归问题的时间复杂度通常是(并不总是)形如,的形式,其中branches是指递归分支数,depth是指递归深度。
branches
depth
以上面的代码及图为例:每次递归计算总往下分成 2 个分支,因此branches = 2,而递归的层数一共有 n 层,所以depth = n,综合起来,即可得时间复杂度为。
branches = 2
depth = n
我们再看一个例子,斐波拉契数列。
求第 n 个斐波拉契数列的值可以用以下算法。
function fib(n) { if (n === 0) { return 0; } else if (n === 1) { return 1; } else { return fib(n - 1) + fib(n - 2); } }
同样的,这个算法的分支为 2,递归深度为 n,所以其时间复杂度也为。
如果一个算法的时间复杂度的函数表达式可以写成下面的这种形式:
那么可以通过比较 与 的大小来确定时间复杂度。
比如说二分搜索,它的时间复杂度的函数表达式可写成的形式,即,计算可得,符合第二种情况,所以其时间复杂度为。
算法的空间复杂度是指算法需要消耗的空间资源。其计算和表示方法与时间复杂度类似,一般都用复杂度的渐近性来表示。
例如创建一个长度为n的数组,需要的空间,创建一个的二维数组,需要的空间。
我们在评价一个算法时,需要结合时间复杂度和空间复杂度来综合判断,不过大多数的情况下,只分析算法的时间复杂度,空间复杂度的成本比时间复杂度低。
在空间复杂度成本在可接受范围内时,通常倾向于拿空间换时间,用空间复杂度的增加来减少时间复杂度。
如有错误之处,欢迎指出。
The text was updated successfully, but these errors were encountered:
No branches or pull requests
算法复杂度的概念
通常在评价一个算法的时候,要做两项分析。第一是分析算法的正确性,如果一个算法没有通过正确性验证,那就是无意义的;第二是算法复杂度的分析,算法复杂度能很大程度上反应算法的优劣。
算法的复杂度又分为时间复杂度和空间复杂度。
大多数的情况下,更多的是考虑时间复杂度。
时间复杂度
在计算机科学中,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大 O 符号表述,不包括这个函数的低阶项和首项系数。
时间复杂度是以算法输入值规模 n 为自变量的函数: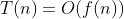 。
。
时间复杂度的表达
表达符号
时间复杂度的表达方式一共有3种,分别为:
通常的情况下,我们用 O 来表达算法的时间复杂度
时间复杂度函数的舍弃项
当我们得到一个算法时间复杂度的函数表达式时,需要对其常数项和次要项进行舍弃,以得到最终的时间复杂度表达式。
当我们得到下面这个时间复杂度的函数表达式时
我们需进行常数项和次要项的舍弃,最终结果为:
接下看一张图。
图中增长速度越快的表达式的级别越高,当算法时间复杂度的函数表达式同时拥有图中多种表达式时,只保留级别最高的表达式,其余的当做次要项舍弃。
例如:
计算时间复杂度(一般问题)
在计算时间复杂度的时候,一般要考虑以下几点:
看几个例子:
从上面的代码可以知道,基本操作就是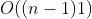 ,去除常数项和次要项,算法时间复杂度为
,去除常数项和次要项,算法时间复杂度为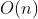 。
。
if操作,时间复杂度为1;当我们假设n = array.length时,基本操作被执行的次数就是n-1次,所以其时间复杂度为再来看看复合操作的例子。
demo2 中,先遍历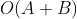 。而在 demo3 中,每进行一次
。而在 demo3 中,每进行一次 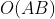 。
。
arrA,再遍历arrB,所以其时间复杂度应该是相加的,为arrA的取值,都要将arrB遍历一遍,所以其时间复杂度应该是相乘的,为来看一个 demo3 的变种:
假设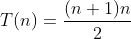 ,经过去除常数项和次要项,最终得到时间复杂度为
,经过去除常数项和次要项,最终得到时间复杂度为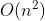 。
。
arr.length = n,那么我们可以推导出,外侧for循环第一次执行时,内侧for循环里面的代码会被执行n次;外侧循环第二次自执行时,内侧循环的代码会被执行n-1次;依次类推,内侧循环代码会依次被执行n-2、n-3、……、2、1,这是一个等差数列,对其进行求和,得到算法时间复杂度的函数表达式为时间复杂度(递归问题)
什么是递归?
递归,又译为递回,在数学与计算机科学中,是指在函数的定义中使用函数自身的方法。递归一词还较常用于描述以自相似方法重复事物的过程。例如,当两面镜子相互之间近似平行时,镜中嵌套的图像是以无限递归的形式出现的。也可以理解为自我复制的过程。
比如说阶乘就可以用递归来求,看代码。
当我们求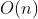 。
。
n的阶乘时,demo(n) = n * demo(n-1),需要先求n-1的阶乘。推导下去,需要依次计算(n-1)、(n-2)、……、2、1阶乘,且每次只做一次乘法运算,最后一次直接赋值,所以需要做n次运算,所以时间复杂度为再看一个代码。
当要计算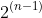 个
个
demo5(n)时,就需要先去计算demo5(n-1) + demo5(n-1);依次类推,最后需要计算demo5(1)。将所有需要计算的项用下图来表示:那么需要进行计算的次数为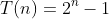 ,经过计算之后去除常数项和次要项,最终时间复杂度为
,经过计算之后去除常数项和次要项,最终时间复杂度为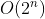 。
。
1、2、4、……、2^(n-1),为一个等比数列,每次基本操作计算的时间复杂度为1,那么整个时间复杂度的函数表达式为结论
对于递归问题的时间复杂度,有一个经验性结论:递归问题的时间复杂度通常是(并不总是)形如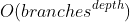 ,的形式,其中
,的形式,其中
branches是指递归分支数,depth是指递归深度。以上面的代码及图为例:每次递归计算总往下分成 2 个分支,因此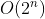 。
。
branches = 2,而递归的层数一共有 n 层,所以depth = n,综合起来,即可得时间复杂度为我们再看一个例子,斐波拉契数列。
求第 n 个斐波拉契数列的值可以用以下算法。
同样的,这个算法的分支为 2,递归深度为 n,所以其时间复杂度也为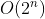 。
。
时间复杂度主定理
如果一个算法的时间复杂度的函数表达式可以写成下面的这种形式:
那么可以通过比较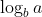 与
与  的大小来确定时间复杂度。
的大小来确定时间复杂度。
比如说二分搜索,它的时间复杂度的函数表达式可写成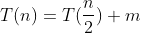 的形式,即
的形式,即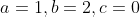 ,计算可得
,计算可得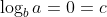 ,符合第二种情况,所以其时间复杂度为
,符合第二种情况,所以其时间复杂度为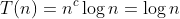 。
。
空间复杂度
算法的空间复杂度是指算法需要消耗的空间资源。其计算和表示方法与时间复杂度类似,一般都用复杂度的渐近性来表示。
例如创建一个长度为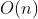 的空间,创建一个
的空间,创建一个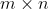 的二维数组,需要
的二维数组,需要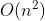 的空间。
的空间。
n的数组,需要结语
我们在评价一个算法时,需要结合时间复杂度和空间复杂度来综合判断,不过大多数的情况下,只分析算法的时间复杂度,空间复杂度的成本比时间复杂度低。
在空间复杂度成本在可接受范围内时,通常倾向于拿空间换时间,用空间复杂度的增加来减少时间复杂度。
如有错误之处,欢迎指出。
The text was updated successfully, but these errors were encountered: