noj实验10报告.md

noj实验10报告

0.0 题目//需求分析

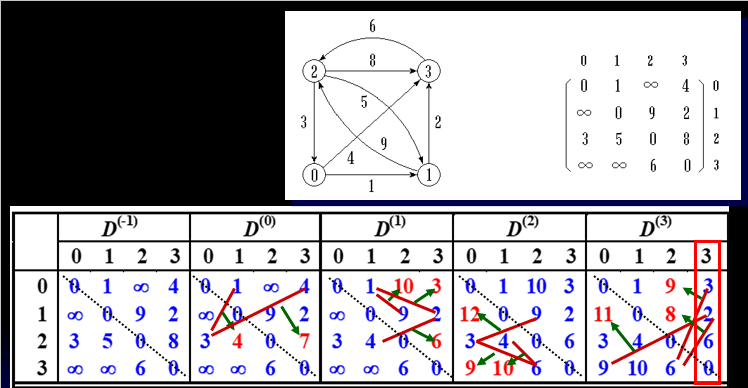
需求分析：用弗洛伊德算法构建每个结点间的最短路径。

1.0 实验思路

存储结构和以前的都一样。

就是一个起始点一列一列从上到下遍历，中点随起始点的遍历更新终点步数，终点就是起点和中点在矩阵中的交叉点，最后按需输出就可以。

2.0 代码

#include <stdio.h>
#include <stdlib.h>
 
struct graphList
{
    int vexNum;
    int graph[120][120];
};
 
void createNewGraphList (struct graphList *gList);
void floydAlgorithm(struct graphList *gList);
void putOut(struct graphList *gList);
 
int main()
{
    struct graphList gList;
    createNewGraphList (&gList);//创建图
    floydAlgorithm (&gList);//计算路径
    putOut (&gList);//按需输出
    return 0;
}
 

void createNewGraphList(struct graphList *gList)
{
    int i,j;
    scanf ("%d", &(gList -> vexNum));//结点数
    for (i=0;i < gList->vexNum; i++)
    {
        for (j = 0; j < gList -> vexNum; j++)
        {
            scanf ("%d", &(gList -> graph[i][j]));//遍历输入权重
        }
    }
}
 
void floydAlgorithm(struct graphList *gList)
{
    int maxVexNum = gList -> vexNum;
    int startI, startJ;
    int midI, midJ;
    int endI, endJ, endStep;
    for (startJ = 0; startJ < maxVexNum; startJ++)//起点按列
    {
        for (startI = 0; startI < maxVexNum; startI++)//起点按行
        {
            if (gList -> graph[startI][startJ] > 0 && gList -> graph[startI][startJ] < 10000)//若有权值（有路走）
            {
                midI = startJ;//中点坐标
                for (midJ = 0; midJ < maxVexNum; midJ++)//中点按列
                {
                    if (gList -> graph[midI][midJ] > 0 && gList -> graph[midI][midJ] < 10000)//若有权值（有路走）
                    {
                        endI = startI;//终点为交叉点
                        endJ = midJ;
                        endStep = gList -> graph[startI][startJ] + gList -> graph[midI][midJ];
                        if (endStep < gList -> graph[endI][endJ])//若新路步数较少，就更新
                        {
                            gList -> graph[endI][endJ] = endStep;
                        }
                    }
                }
            }
        }
    }
}
void putOut(struct graphList *gList)
{
    int n;
    int i, j;
    scanf ("%d", &n);//需输出的个数
    while (n--)
    {
        scanf ("%d%d", &i, &j);
        printf ("%d\n", gList -> graph[i][j]);//输出
    }
}

3.0 心得

掌握了弗洛伊德算法。

解决了一些指针问题。