1572.md

title	description	keywords
1572. 矩阵对角线元素的和	LeetCode 1572. 矩阵对角线元素的和题解，Matrix Diagonal Sum，包含解题思路、复杂度分析以及完整的 JavaScript 代码实现。	LeetCode 1572. 矩阵对角线元素的和 矩阵对角线元素的和 Matrix Diagonal Sum 解题思路 数组 矩阵

1572. 矩阵对角线元素的和

🟢 Easy  🔖  数组 矩阵  🔗 力扣 LeetCode

题目

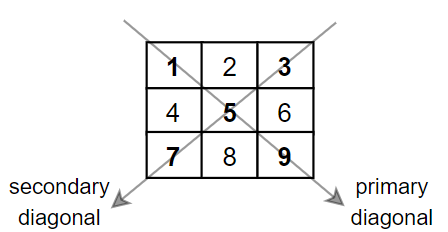
Given a square matrix mat, return the sum of the matrix diagonals.

Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.

Example 1:

Input:

mat = [
  [1, 2, 3],

  [4, 5, 6],

  [7, 8, 9]]

Output: 25

Explanation: Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25

Notice that element mat[1][1] = 5 is counted only once.

Example 2:

Input:

mat = [
	[1, 1, 1, 1],

	[1, 1, 1, 1],

	[1, 1, 1, 1],

	[1, 1, 1, 1]
];

Output: 8;

Example 3:

Input: mat = [[5]]

Output: 5

Constraints:

• n == mat.length == mat[i].length
• 1 <= n <= 100
• 1 <= mat[i][j] <= 100

题目大意

给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

示例 1：

输入：

mat = [
  [1, 2, 3],

  [4, 5, 6],

  [7, 8, 9]]

输出： 25

解释： 对角线的和为：1 + 5 + 9 + 3 + 7 = 25

请注意，元素 mat[1][1] = 5 只会被计算一次。

示例 2：

输入：

mat = [
	[1, 1, 1, 1],

	[1, 1, 1, 1],

	[1, 1, 1, 1],

	[1, 1, 1, 1]
];

输出： 8

示例 3：

输入： mat = [[5]]

输出： 5

提示：

• n == mat.length == mat[i].length
• 1 <= n <= 100
• 1 <= mat[i][j] <= 100

解题思路

1. 定义变量：

   • n：矩阵的大小。
   • j1 和 j2：分别指向矩阵对角线的列索引，初始值为 0 和 n - 1。
   • sum：用于存储对角线元素的累加和。

2. 遍历矩阵：

   • 通过循环，从第 0 行到第 n-1 行：
     • 累加主对角线 (mat[i][j1]) 和次对角线 (mat[i][j2]) 元素到 sum。
     • 更新 j1 和 j2，使其分别向右下和左下移动。

3. 处理奇数维矩阵重复计算的情况：

   • 如果矩阵维度 n 为奇数，主对角线和次对角线在中心位置会重复计算一次。
   • 找到中心点的索引 mid = Math.floor(n / 2)，并从 sum 中减去该元素 mat[mid][mid]。

4. 返回最终的和：

   • 返回 sum，即对角线的总和。

复杂度分析

• 时间复杂度： O(n)，矩阵的行数决定了循环次数。
• 空间复杂度： O(1)，只使用了常量级额外空间。

代码

/**
 * @param {number[][]} mat
 * @return {number}
 */
var diagonalSum = function (mat) {
	const n = mat.length;
	let sum = 0;

	// 遍历矩阵，累加主对角线和次对角线的值
	for (let i = 0; i < n; i++) {
		sum += mat[i][i] + mat[i][n - 1 - i];
	}

	// 如果矩阵维度为奇数，减去重复的中心值
	if (n % 2 === 1) {
		const mid = Math.floor(n / 2);
		sum -= mat[mid][mid];
	}

	return sum;
};

相关题目

题号	标题	题解	标签	难度	力扣
2133	检查是否每一行每一列都包含全部整数	[✓]	数组 哈希表 矩阵	🟢	🀄️ 🔗
2319	判断矩阵是否是一个 X 矩阵	[✓]	数组 矩阵	🟢	🀄️ 🔗