This is a C-library for linear algebra which is meant to be used for embedded systems such as AVR, PIC, ARM etc. The library is built easily and follows the MATLAB/Octave "standard" as much as it can when computing and solving matrices. This C-library uses Lapack subroutines from Lapack version 3.2.1 and I have changed this Lapack library so it does not require a specific CPU/computer or asking for an operating system. I want this library to have 100% portability.
- Easy to use in the editor
- Basic easy code to read if needed
- Follows MATLAB commands as much as it can
- Can be used with a compiler as low as C99 standard, default is C11
- Simple use for most common matrix algebra
- Using minimal but necessary Lapack subroutines as possible due to the small amout of flash memory it will be loaded into.
If you are looking for an even smaller library that performs the same job (except for imaginary eigenvectors), then CControl will be a good alternative. CControl is more applied and contains lots of examples such as system identification, path finding, linear algebra, filtering, control engineering, optimization etc. CControl does not use LAPACK therefore it fits even on smaller microcontrollers. Please fork and star so more people can see CControl.
2023-07-31: This library is now supporting LAPACK for embedded systems. https://github.com/DanielMartensson/CControl
Support for this project is ongoing and is subject to found bugs or when new features are added otherwise everything on the main branch is currently functional.
- Windows 7 MinGW 64 bit
- Ubuntu Linux GCC 64 bit
- Raspberry Pi B+/Zero W GCC-ARM 32 bit
- STM32 GCC-ARM-Atollic 32 bit
Step 1: Download EmbeddedLapack folder
Step 2: Open EmbeddedLapack and go to Debug folder
Step 3: Execute this to compile
make clean
make
Step 1: Download EmbeddedLapack folder
Step 2: Move the folders "Lapack" and "LinearAlgebra" from the folder EmbeddedLapack -> src, to the same folder as your main.c file is located.
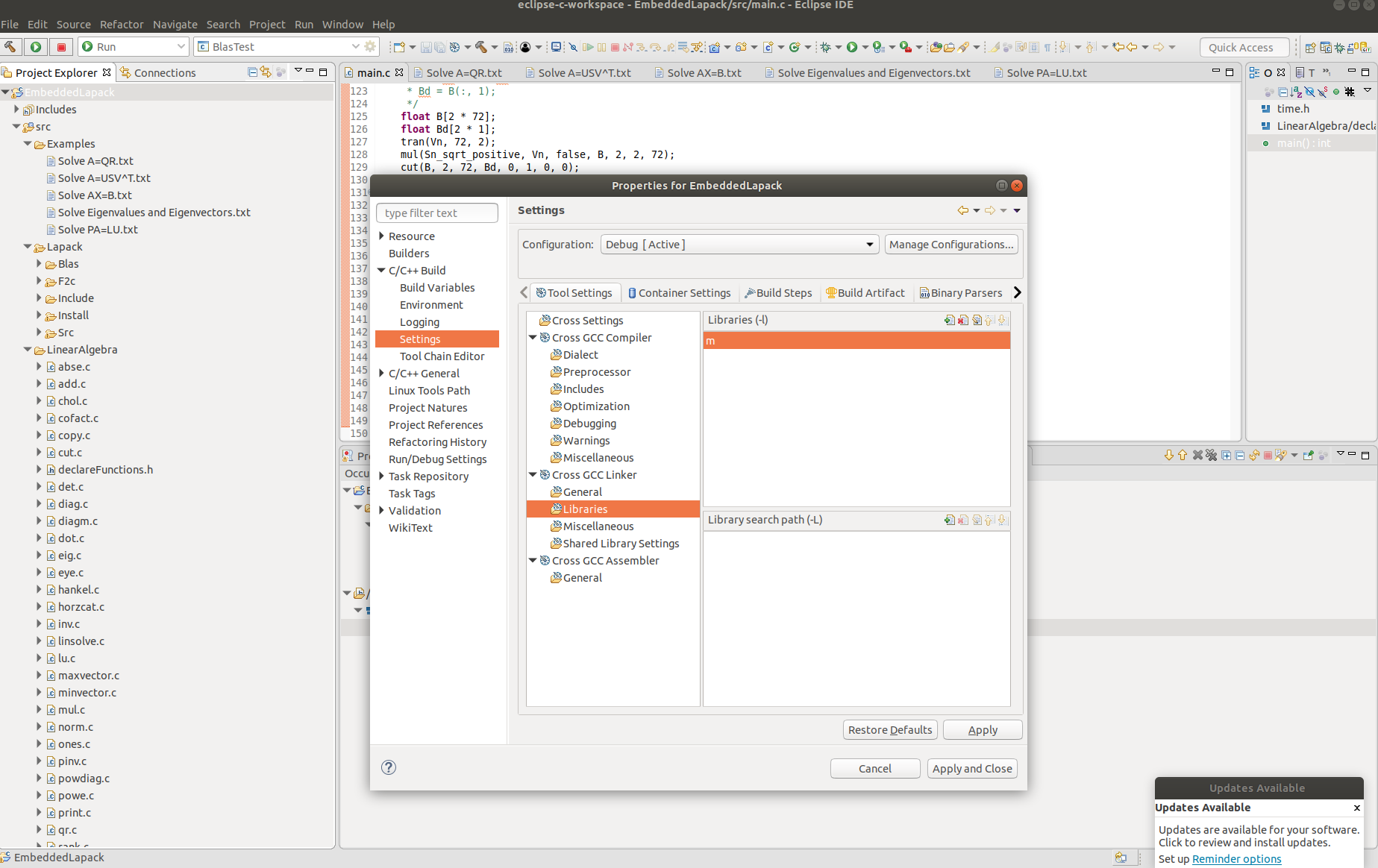
Step 3: Link "-lm" like this.
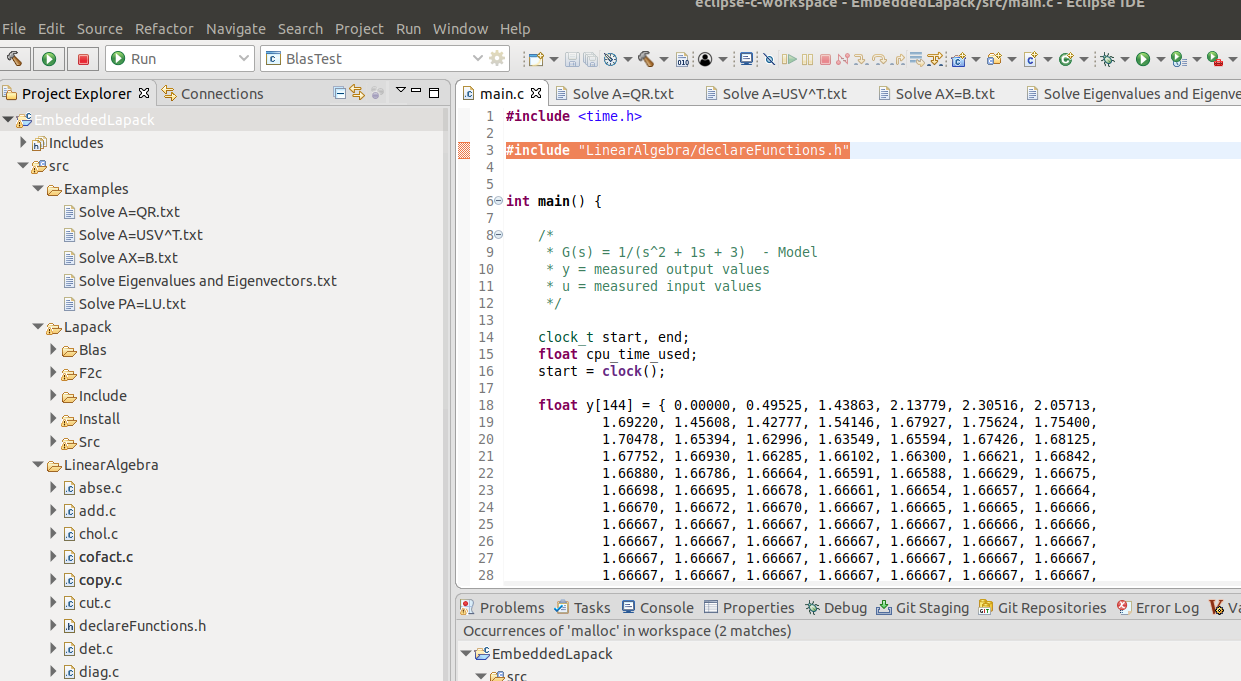
Step 4: Paste in "#include "LinearAlgebra/declareFunctions.h"" in top of your main.c file
Done! Now you can compile.
void tran(double* A, int row, int column);
void print(double* A, int row, int column);
void linsolve(double* A, double* X, double* B, int row, int column_b);
void svd(double* A, double* U, double* S, double* V, int row, int column);
void diag(double* A, double* B, int row_b, int column_b);
void qr(double* A, double* Q, double* R, int row, int column);
void triu(double* A, double* B, int shift, int row, int column);
void eye(double* A, int row, int column);
void mul(double* A, double* B, bool elementWise, double* C, int row_a, int column_a, int column_b);
void scale(double* A, double scalar, int row, int column);
void sub(double* A, double* B, double* C, int row_a, int column_a, int column_b);
void lu(double* A, double* L, double* U, double* P, int row, int column);
void tril(double* A, double* B, int shift, int row, int column);
void inv(double* A, int row);
void chol(double* A, double* L, int row);
double det(double *A, int row);
void toeplitz(double* A, double* B, int length);
void hankel(double* A, double* H, int length, int step);
void cut(double* A, int row, int column, double* B, int start_row, int stop_row, int start_column, int stop_column);
void diagpower(double* A, double p, int row, int column);
void eabs(double* A, int row, int column);
void add(double* A, double* B, double* C, int row_a, int column_a, int column_b);
void copy(double* A, double* B, int row, int column);
void cofact(double* A, double* CO, int row, int column);
void mdiag(double* A, double* B, int row, int column);
double dot(double* A, double* B, int row);
void horzcat(double* A, double* B, double* C, int row_a, int column_a, int column_b);
void maxvector(double* A, int row, double* val, int* index);
void minvector(double* A, int row, double* val, int* index);
double norm(double* A, int row, char* P);
void ones(double* A, int row, int column);
void pinv(double* A, int row, int column);
void power(double* A, int row, int column, double value);
void repmat(double* A, int row, int column, int horz, int vert, double* B);
void sqrte(double* A, int row, int column);
void sumrows(double* A, double* B, int row, int column);
void vec(double* A, double* B, int row, int column);
void vertcat(double* A, double* B, double* C, int row_a, int column_a, int row_b);
void zeros(double* A, int row, int column);
int rank(double* A, int row);
void eig(double* A, double* Ereal, double* Eimag, double* Vreal_left, double* Vimag_left, double* Vreal_right, double* Vimag_right, int row);
void mpower(double* A, int row, int n);
void insert(double* A, double* B, int row_a, int column_a, int column_b, int startRow_b, int startColumn_b);
void move(double* A, int row, int column, int down, int right);
void quadprog(double* H, double* g, double* A, double* ulb_vec, double* uub_vec, double* ylb_vec, double* yub_vec, int* nWSR, double* u, int columnH, int rowA);
void linprog(double* c, double* A, double* b, double* x, int row_a, int column_a, uint8_t max_or_min, int iteration_limit);
When you compile this, you need to take respect on this.
#include <math.h> // Need be linked with "-lm" when compiling this code
Also you need to link the folder "Include" located inside EmbeddedLapack -> src -> Lapack.
If you declare a matrix or a vector and you use that with this library, but you getting garbage values back. Try to sett all values of the matrix or vector to zeros by using:
zeros(A, row, column);
Most of my functions have this algorithm included in the beginning of the functions.
Here is some examples how to use
#include <time.h>
#include "LinearAlgebra/declareFunctions.h"
int main() {
clock_t start, end;
float cpu_time_used;
start = clock();
// A matrix with size 6 x 4
double A[6*4] = {0.674878, 0.151285, 0.875139, 0.150518,
0.828102, 0.150747, 0.934674, 0.474325,
0.476510, 0.914686, 0.740681, 0.060455,
0.792594, 0.471488, 0.529343, 0.743405,
0.084739, 0.475160, 0.419307, 0.628999,
0.674878, 0.151285, 0.875139, 0.150518};
double Q[6*6];
double R[6*4];
// Solve
qr(A, Q, R, 6, 4);
// Print
print(A, 6,4);
print(Q, 6,6);
print(R, 6,4);
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
#include <time.h>
#include "LinearAlgebra/declareFunctions.h"
#define row 17
#define column 15
int main( )
{
clock_t start, end;
float cpu_time_used;
start = clock();
double A[row*column] = {
0.84245, 0.23405 , 0.69751 , 0.27905 , 0.18851 , 0.61018 , 0.62182 , 0.71839 , 0.79161 ,0.56156 , 0.83395 , 0.092388 , 0.8511 , 0.44826 , 0.82158,
0.84614 , 0.15947 , 0.096336 , 0.80793 , 0.35114 , 0.42583 , 0.2134 , 0.75324 , 0.31391 , 0.22892 , 0.94773 , 0.81204 , 0.62554 , 0.28367 , 0.26637,
0.26509 , 0.91429 , 0.14222 , 0.28321 , 0.11607 , 0.41188 , 0.10071 , 0.18224 , 0.75723 , 0.89125 , 0.62494 , 0.83016 , 0.46448 , 0.73119 , 0.10982,
0.45197 , 0.44562 , 0.27909 , 0.76019 , 0.014571 , 0.42705 , 0.70214 , 0.64936 , 0.98451 , 0.59632 , 0.07654 , 0.95633 , 0.18574 , 0.92716 , 0.65401,
0.48034 , 0.38327 , 0.32906 , 0.34794 , 0.68673 , 0.54113 , 0.34142 , 0.48561 , 0.37221 , 0.16097 , 0.15569 , 0.63287 , 0.17518 , 0.055447 , 0.44536,
0.54119 , 0.34478 , 0.53297 , 0.2796 , 0.95212 , 0.5353 , 0.8202 , 0.32707 , 0.0062771 , 0.64993 , 0.057361 , 0.59959 , 0.16867 , 0.67892 , 0.52882,
0.082573 , 0.96676 , 0.080315 , 0.48813 , 0.33496 , 0.4436 , 0.01436 , 0.89664 , 0.49167 , 0.37092 , 0.31586 , 0.54683 , 0.65159 , 0.38531 , 0.20697,
0.35775 , 0.42437 , 0.79392 , 0.49724 , 0.01319 , 0.0074932 , 0.66462 , 0.6506 , 0.9889 , 0.27213 , 0.99607 , 0.68418 , 0.70238 , 0.81493 , 0.46062,
0.22609 , 0.59924 , 0.74631 , 0.81566 , 0.92784 , 0.47376 , 0.83531 , 0.47031 , 0.97093 , 0.44778 , 0.42997 , 0.71882 , 0.36504 , 0.34216 , 0.95187,
0.87475 , 0.22003 , 0.71901 , 0.90968 , 0.27265 , 0.16106 , 0.21283 , 0.14918 , 0.16776 , 0.83038 , 0.43605 , 0.85075 , 0.54771 , 0.77479 , 0.24739,
0.21203 , 0.65616 , 0.63534 , 0.57569 , 0.22113 , 0.48063 , 0.24207 , 0.54873 , 0.25042 , 0.82671 , 0.88986 , 0.41674 , 0.95235 , 0.89875 , 0.15004,
0.86164 , 0.89058 , 0.66423 , 0.60958 , 0.47708 , 0.18674 , 0.66359 , 0.92383 , 0.48073 , 0.79466 , 0.64519 , 0.69876 , 0.0066587 , 0.55114 , 0.10979,
0.35586 , 0.94772 , 0.28888 , 0.63119 , 0.42774 , 0.82597 , 0.90274 , 0.40152 , 0.96414 , 0.84376 , 0.028355 , 0.040771 , 0.85359 , 0.92875 , 0.32352,
0.39274 , 0.27788 , 0.41549 , 0.90884 , 0.042767 , 0.64168 , 0.086933 , 0.47941 , 0.91491 , 0.26425 , 0.11667 , 0.49996 , 0.12644 , 0.87136 , 0.30768,
0.86527 , 0.92393 , 0.47957 , 0.32175 , 0.87965 , 0.13719 , 0.4014 , 0.25277 , 0.83936 , 0.73476 , 0.97174 , 0.65243 , 0.85813 , 0.62705 , 0.0013063,
0.34355 , 0.43424 , 0.34352 , 0.34341 , 0.94343 , 0.45452 , 0.343 , 0.1243 , 0.12522 , 0.214343 , 0.12432 , 0.54534 , 0.12442 , 0.12467 , 0.9988,
0.84245, 0.23405 , 0.69751 , 0.27905 , 0.18851 , 0.61018 , 0.62182 , 0.71839 , 0.79161 ,0.56156 , 0.83395 , 0.092388 , 0.8511 , 0.44826 , 0.82158};
double U[row*row];
double S[row*column];
double V[column*column];
// Solve
svd(A, U, S, V, row, column);
// print
print(U, row, row);
print(S, row, column);
print(V, column, column);
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
#include <time.h>
#include "LinearAlgebra/declareFunctions.h"
int main( )
{
clock_t start, end;
float cpu_time_used;
start = clock();
/*
* A matrix 3x3 - Need to be square
*/
double A[3*3] = {3, 4, 1,
6, 10, 2,
5, 3, 2
};
/*
* Solution 3x4
*/
double X[3*4];
/*
* B matrix 3x4
*/
double B[3*4] = {4, 3, 22, 5,
5, 3, 2, 5,
3, 4, 5, 3};
/*
* Solve
*/
linsolve(A, X, B, 3, 4); // 3 = A row, 4 = B column
/*
* Print solution
*/
print(X, 3, 4);
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
#include <time.h>
#include "LinearAlgebra/declareFunctions.h"
int main( ) {
clock_t start, end;
float cpu_time_used;
start = clock();
// Need to be square
double A[6*6] = {4,3,1,4,2,23,
6,3,-2,3,5,8,
1,3,6,2,3,2,
2,5,6,7,4,4,
4,6,-88,6,4,6,
2,1,44,54,3,2
};
double Ereal[6]; // Eigenvalues real
double Eimag[6]; // Eigenvalues imag part
double Vreal_left[6*6]; // Eigenvectors real left
double Vimag_left[6*6]; // Eigenvectors imag left
double Vreal_right[6*6]; // Eigenvectors real right
double Vimag_right[6*6]; // Eigenvectors imag right
// Solve
eig(A,Ereal,Eimag,Vreal_left,Vimag_left,Vreal_right,Vimag_right,6);
// Print
print(A, 6, 6);
print(Ereal, 6, 1);
print(Eimag, 6, 1);
print(Vreal_left, 6,6);
print(Vimag_left, 6,6);
print(Vreal_right, 6,6);
print(Vimag_right, 6,6);
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
#include <time.h>
#include "LinearAlgebra/declareFunctions.h"
int main( ) {
clock_t start, end;
float cpu_time_used;
start = clock();
double A[5*4] = {2, 7, 6, 2,
9, 5, 1, 3,
4, 3, 8, 4,
5, 6, 7, 8,
2, 2, -3,-1
};
double U[4*4];
double L[5*4];
double P[5*5];
// Solve
lu(A, L, U, P, 5, 4);
// Print
print(A, 5,4);
print(U, 4,4);
print(L, 5,4);
print(P, 5,5);
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
This will estimate a 2x2 state space model from measurement data
#include <time.h>
#include "LinearAlgebra/declareFunctions.h"
int main() {
/*
* G(s) = 1/(s^2 + 1s + 3) - Model
* y = measured output values
* u = measured input values
*/
clock_t start, end;
float cpu_time_used;
start = clock();
double y[144] = { 0.00000, 0.49525, 1.43863, 2.13779, 2.30516, 2.05713,
1.69220, 1.45608, 1.42777, 1.54146, 1.67927, 1.75624, 1.75400,
1.70478, 1.65394, 1.62996, 1.63549, 1.65594, 1.67426, 1.68125,
1.67752, 1.66930, 1.66285, 1.66102, 1.66300, 1.66621, 1.66842,
1.66880, 1.66786, 1.66664, 1.66591, 1.66588, 1.66629, 1.66675,
1.66698, 1.66695, 1.66678, 1.66661, 1.66654, 1.66657, 1.66664,
1.66670, 1.66672, 1.66670, 1.66667, 1.66665, 1.66665, 1.66666,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66666, 1.66666,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667 };
double u[144] = { 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5 };
// Toeplitz matrix
double toe[144 * 144];
toeplitz(u, toe, 144);
// Upper triangular
double tru[144 * 144];
triu(toe, tru, 0, 144, 144);
// inverse
inv(tru, 144);
// Multiplication
double g[144];
mul(y, tru, false, g, 1, 144, 144);
// Create hankel
double H0[144 * 144];
hankel(g, H0, 144, 1);
double H1[144 * 144];
hankel(g, H1, 144, 2);
// Cut hankel into half
double H0_half[72 * 72];
double H1_half[72 * 72];
cut(H0, 144, 144, H0_half, 0, 71, 0, 71);
cut(H1, 144, 144, H1_half, 0, 71, 0, 71);
// Do SVD
double U[72 * 72];
double S[72 * 72];
double V[72 * 72];
svd(H0_half, U, S, V, 72, 72);
// Model reduction to second order model
double Un[72 * 2];
double Sn[2 * 2];
double Vn[72 * 2];
cut(U, 72, 72, Un, 0, 71, 0, 1);
cut(S, 72, 72, Sn, 0, 1, 0, 1);
cut(V, 72, 72, Vn, 0, 71, 0, 1);
// Create A, B, C
double Sn_sqrt_negative[2 * 2];
double Sn_sqrt_positive[2 * 2];
copy(Sn, Sn_sqrt_negative, 2,2);
copy(Sn, Sn_sqrt_positive, 2,2);
diagpower(Sn_sqrt_negative, -0.5, 2, 2);
diagpower(Sn_sqrt_positive, 0.5, 2, 2);
/*
* C = Un*Sn^(1/2);
* Cd = C(1, 1:2)
*/
double C[72 * 2];
double Cd[1 * 2];
mul(Un, Sn_sqrt_positive, false, C, 72, 2, 2);
cut(C, 72, 2, Cd, 0, 0, 0, 1);
/*
* Ad = Sn^(-1/2)*Un'*H1*Vn*Sn^(-1/2);
*/
double A[72 * 2];
double A1[72 * 2];
double Ad[2 * 2];
double Ad1[2 * 2];
mul(Vn, Sn_sqrt_negative, false, A, 72, 2, 2);
mul(H1_half, A, false, A1, 72, 72, 2);
tran(Un, 72, 2);
mul(Un, A1, false, Ad1, 2, 72, 2);
mul(Sn_sqrt_negative, Ad1, false, Ad, 2, 2, 2);
/*
* B = Sn^(1/2)*Vn'
* Bd = B(:, 1);
*/
double B[2 * 72];
double Bd[2 * 1];
tran(Vn, 72, 2);
mul(Sn_sqrt_positive, Vn, false, B, 2, 2, 72);
cut(B, 2, 72, Bd, 0, 1, 0, 0);
/*
* Print A, B, C
*/
printf("A Matrix: \n");
print(Ad, 2, 2);
printf("B Matrix: \n");
print(Bd, 2, 1);
printf("C Matrix: \n");
print(Cd, 1, 2);
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
Given a state space model and a reference point, this example can compute your best input signals U depending on how you set your control- and predictive horizons column_o and column_h
#include <time.h>
#include "LinearAlgebra/declareFunctions.h"
/*
* Here you can set the sizes for the matrices
*/
#define row_a 2 // A row
#define column_a 2 // A column
#define row_b 2 // B row, the same row as A.
#define column_b 1 // B column, the same column as D
#define row_c 1 // C row, the same row as D
#define column_c 2 // C column, the same column as A
/*
* Create a state space model - discrete
*/
double A[row_a * column_a] = { -0.099272, 0.029481,
-0.088444, -0.158234};
double B[row_b * column_b] = { 0.366424,
0.029481
};
double C[row_c * column_c] = {1, 0};
double D[row_c * column_b] = {0};
double X[row_a] = {0, 0};
double R = 6;
// Create the length of the observability matrix, notice it will have the dimension (row_o * row_c + row_c) x column_b
#define row_o 20
// Create the widt of the lower triangular toeplitz H matrix, notice that it will have the dimension (row_o * row_c + row_c) x (column_h * column_b)
#define column_h 19 // column_h < row_o - always!
// Define the column of the reference vector - Standard is 1
#define column_ry 1
int main() {
/*
* Model predictive control
*/
clock_t start, end;
float cpu_time_used;
start = clock();
/*
* Create the Observabillity matrix and the
*/
double O[(row_o * row_c) * row_a];
double O_[(row_o * row_c) * row_a]; // This is for the lower triangular toeplitz matrix
double A_[row_a * column_a];
double C_[row_c * column_c];
for (int i = 1; i <= row_o; i++) {
copy(A, A_, row_a, column_a); // Copy A -> A_
mpower(A_, row_a, i); // Power A_^i
mul(C, A_, false, C_, row_c, column_c, column_a); // C_ = C*A_
insert(C_, O, row_c, column_c, row_a, (i-1)*row_c, 0); // Insert O = [CA^1; CA^2; CA^3; ... ; CA^row_o];
copy(A, A_, row_a, column_a); // Copy A -> A_
mpower(A_, row_a, i - 1); // Power A_^(i-1)
mul(C, A_, false, C_, row_c, column_c, column_a); // C_ = C*A_
insert(C_, O_, row_c, column_c, row_a, (i-1)*row_c, 0); // Insert O_ = [CA^0; CA^1; CA^2; ... ; CA^(row_o-1)];
}
//print(O, row_o * row_c, row_a);
/*
* Create the lower triangular toeplitz matrix
*/
double H[(row_o * row_c) * (column_h * column_b)];
zeros(H, row_o * row_c, column_h * column_b);
// T = O_*B - Observabillity matrix times B
double T[(row_o * row_c) * column_b];
mul(O_, B, false, T, row_o * row_c, row_a, column_b);
// Lower triangular toeplitz matrix of T = [C*A^0*B; C*A^1*B; C*A^2*B; C*A^3*B; ...; C*A^(row_o-1)*B]
for (int j = 0; j < column_h; j++){
insert(T, H, row_o * row_c, column_b, column_h * column_b, 0, j*column_b);
move(T, row_o * row_c, column_b, row_c , 0);
}
//print(H, row_o * row_c, column_h * column_b); // H matrix
/*
* Compute U = pinv(H)*(Ry*R - O*X), where R is our reference vector, X is our initial state vector
*/
pinv(H, row_o * row_c, column_h * column_b); // Pseudo inverse of H. Using the SVD method
double Ry[(row_o * row_c)*column_ry];
ones(Ry, row_o * row_c, column_ry);
scale(Ry, R, row_o * row_c, column_ry); // Ry*R = Ry
double OX[(row_o * row_c)*column_ry];
mul(O, X, false, OX, row_o * row_c, row_a, column_ry); // O*X
double Ry_OX[(row_o * row_c)*column_ry];
sub(Ry, OX, Ry_OX, row_o * row_c, column_ry, column_ry); // Ry-O*X
double U[(column_h * column_b)*column_ry];
mul(H, Ry_OX, false, U, column_h * column_b, row_o * row_c, column_ry); // U = pinv(H)*(Ry-O*X);
/*
* Our best input values
*/
print(U, column_h * column_b, column_ry);
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
Here is a simulation of a step response that turning into an impulse response. Then we take the SVD of that impulse response.
13:15:53 **** Incremental Build of configuration Debug for project EmbeddedLapack ****
make all
Building file: ../src/main.c
Invoking: Cross GCC Compiler
gcc -std=c11 -O2 -g3 -Wall -c -fmessage-length=0 -MMD -MP -MF"src/main.d" -MT"src/main.o" -o "src/main.o" "../src/main.c"
Finished building: ../src/main.c
Building target: EmbeddedLapack
Invoking: Cross GCC Linker
gcc -o "EmbeddedLapack" ./src/LinearAlgebra/add.o ./src/LinearAlgebra/chol.o ./src/LinearAlgebra/cofact.o ./src/LinearAlgebra/copy.o ./src/LinearAlgebra/cut.o ./src/LinearAlgebra/det.o ./src/LinearAlgebra/diag.o ./src/LinearAlgebra/diagpower.o ./src/LinearAlgebra/dot.o ./src/LinearAlgebra/eabs.o ./src/LinearAlgebra/eig.o ./src/LinearAlgebra/eye.o ./src/LinearAlgebra/hankel.o ./src/LinearAlgebra/horzcat.o ./src/LinearAlgebra/insert.o ./src/LinearAlgebra/inv.o ./src/LinearAlgebra/linsolve.o ./src/LinearAlgebra/lu.o ./src/LinearAlgebra/maxvector.o ./src/LinearAlgebra/mdiag.o ./src/LinearAlgebra/minvector.o ./src/LinearAlgebra/move.o ./src/LinearAlgebra/mpower.o ./src/LinearAlgebra/mul.o ./src/LinearAlgebra/norm.o ./src/LinearAlgebra/ones.o ./src/LinearAlgebra/pinv.o ./src/LinearAlgebra/power.o ./src/LinearAlgebra/print.o ./src/LinearAlgebra/qr.o ./src/LinearAlgebra/rank.o ./src/LinearAlgebra/repmat.o ./src/LinearAlgebra/scale.o ./src/LinearAlgebra/sqrte.o ./src/LinearAlgebra/sub.o ./src/LinearAlgebra/sumrows.o ./src/LinearAlgebra/svd.o ./src/LinearAlgebra/toeplitz.o ./src/LinearAlgebra/tran.o ./src/LinearAlgebra/tril.o ./src/LinearAlgebra/triu.o ./src/LinearAlgebra/vec.o ./src/LinearAlgebra/vertcat.o ./src/LinearAlgebra/zeros.o ./src/Lapack/Scr/dbdsqr.o ./src/Lapack/Scr/dgebak.o ./src/Lapack/Scr/dgebal.o ./src/Lapack/Scr/dgebd2.o ./src/Lapack/Scr/dgebrd.o ./src/Lapack/Scr/dgeev.o ./src/Lapack/Scr/dgehd2.o ./src/Lapack/Scr/dgehrd.o ./src/Lapack/Scr/dgelq2.o ./src/Lapack/Scr/dgelqf.o ./src/Lapack/Scr/dgeqr2.o ./src/Lapack/Scr/dgeqrf.o ./src/Lapack/Scr/dgesv.o ./src/Lapack/Scr/dgesvd.o ./src/Lapack/Scr/dgetf2.o ./src/Lapack/Scr/dgetrf.o ./src/Lapack/Scr/dgetrs.o ./src/Lapack/Scr/dhseqr.o ./src/Lapack/Scr/disnan.o ./src/Lapack/Scr/dlabad.o ./src/Lapack/Scr/dlabrd.o ./src/Lapack/Scr/dlacpy.o ./src/Lapack/Scr/dladiv.o ./src/Lapack/Scr/dlaexc.o ./src/Lapack/Scr/dlahqr.o ./src/Lapack/Scr/dlahr2.o ./src/Lapack/Scr/dlaisnan.o ./src/Lapack/Scr/dlaln2.o ./src/Lapack/Scr/dlange.o ./src/Lapack/Scr/dlanv2.o ./src/Lapack/Scr/dlapy2.o ./src/Lapack/Scr/dlaqr0.o ./src/Lapack/Scr/dlaqr1.o ./src/Lapack/Scr/dlaqr2.o ./src/Lapack/Scr/dlaqr3.o ./src/Lapack/Scr/dlaqr4.o ./src/Lapack/Scr/dlaqr5.o ./src/Lapack/Scr/dlarf.o ./src/Lapack/Scr/dlarfb.o ./src/Lapack/Scr/dlarfg.o ./src/Lapack/Scr/dlarfp.o ./src/Lapack/Scr/dlarft.o ./src/Lapack/Scr/dlarfx.o ./src/Lapack/Scr/dlartg.o ./src/Lapack/Scr/dlas2.o ./src/Lapack/Scr/dlascl.o ./src/Lapack/Scr/dlaset.o ./src/Lapack/Scr/dlasq1.o ./src/Lapack/Scr/dlasq2.o ./src/Lapack/Scr/dlasq3.o ./src/Lapack/Scr/dlasq4.o ./src/Lapack/Scr/dlasq5.o ./src/Lapack/Scr/dlasq6.o ./src/Lapack/Scr/dlasr.o ./src/Lapack/Scr/dlasrt.o ./src/Lapack/Scr/dlassq.o ./src/Lapack/Scr/dlasv2.o ./src/Lapack/Scr/dlaswp.o ./src/Lapack/Scr/dlasy2.o ./src/Lapack/Scr/dorg2r.o ./src/Lapack/Scr/dorgbr.o ./src/Lapack/Scr/dorghr.o ./src/Lapack/Scr/dorgl2.o ./src/Lapack/Scr/dorglq.o ./src/Lapack/Scr/dorgqr.o ./src/Lapack/Scr/dorm2r.o ./src/Lapack/Scr/dormbr.o ./src/Lapack/Scr/dormhr.o ./src/Lapack/Scr/dorml2.o ./src/Lapack/Scr/dormlq.o ./src/Lapack/Scr/dormqr.o ./src/Lapack/Scr/dtrevc.o ./src/Lapack/Scr/dtrexc.o ./src/Lapack/Scr/ieeeck.o ./src/Lapack/Scr/iladlc.o ./src/Lapack/Scr/iladlr.o ./src/Lapack/Scr/ilaenv.o ./src/Lapack/Scr/ilaslc.o ./src/Lapack/Scr/ilaslr.o ./src/Lapack/Scr/iparmq.o ./src/Lapack/Scr/sgebak.o ./src/Lapack/Scr/sgebal.o ./src/Lapack/Scr/sgeev.o ./src/Lapack/Scr/sgehd2.o ./src/Lapack/Scr/sgehrd.o ./src/Lapack/Scr/sgeqr2.o ./src/Lapack/Scr/sgetf2.o ./src/Lapack/Scr/sgetrf.o ./src/Lapack/Scr/shseqr.o ./src/Lapack/Scr/sisnan.o ./src/Lapack/Scr/slabad.o ./src/Lapack/Scr/slacpy.o ./src/Lapack/Scr/sladiv.o ./src/Lapack/Scr/slaexc.o ./src/Lapack/Scr/slahqr.o ./src/Lapack/Scr/slahr2.o ./src/Lapack/Scr/slaisnan.o ./src/Lapack/Scr/slaln2.o ./src/Lapack/Scr/slange.o ./src/Lapack/Scr/slanv2.o ./src/Lapack/Scr/slapy2.o ./src/Lapack/Scr/slaqr0.o ./src/Lapack/Scr/slaqr1.o ./src/Lapack/Scr/slaqr2.o ./src/Lapack/Scr/slaqr3.o ./src/Lapack/Scr/slaqr4.o ./src/Lapack/Scr/slaqr5.o ./src/Lapack/Scr/slarf.o ./src/Lapack/Scr/slarfb.o ./src/Lapack/Scr/slarfg.o ./src/Lapack/Scr/slarfp.o ./src/Lapack/Scr/slarft.o ./src/Lapack/Scr/slarfx.o ./src/Lapack/Scr/slartg.o ./src/Lapack/Scr/slascl.o ./src/Lapack/Scr/slaset.o ./src/Lapack/Scr/slassq.o ./src/Lapack/Scr/slaswp.o ./src/Lapack/Scr/slasy2.o ./src/Lapack/Scr/sorg2r.o ./src/Lapack/Scr/sorghr.o ./src/Lapack/Scr/sorgqr.o ./src/Lapack/Scr/sorm2r.o ./src/Lapack/Scr/sormhr.o ./src/Lapack/Scr/sormqr.o ./src/Lapack/Scr/strevc.o ./src/Lapack/Scr/strexc.o ./src/Lapack/Install/dlamch.o ./src/Lapack/Install/slamch.o ./src/Lapack/F2c/d_lg10.o ./src/Lapack/F2c/d_sign.o ./src/Lapack/F2c/exit_.o ./src/Lapack/F2c/f77_aloc.o ./src/Lapack/F2c/i_nint.o ./src/Lapack/F2c/pow_dd.o ./src/Lapack/F2c/pow_di.o ./src/Lapack/F2c/pow_ri.o ./src/Lapack/F2c/r_lg10.o ./src/Lapack/F2c/r_sign.o ./src/Lapack/F2c/s_cat.o ./src/Lapack/F2c/s_cmp.o ./src/Lapack/F2c/s_copy.o ./src/Lapack/Blas/daxpy.o ./src/Lapack/Blas/dcopy.o ./src/Lapack/Blas/ddot.o ./src/Lapack/Blas/dgemm.o ./src/Lapack/Blas/dgemv.o ./src/Lapack/Blas/dger.o ./src/Lapack/Blas/dnrm2.o ./src/Lapack/Blas/drot.o ./src/Lapack/Blas/dscal.o ./src/Lapack/Blas/dswap.o ./src/Lapack/Blas/dtrmm.o ./src/Lapack/Blas/dtrmv.o ./src/Lapack/Blas/dtrsm.o ./src/Lapack/Blas/idamax.o ./src/Lapack/Blas/isamax.o ./src/Lapack/Blas/lsame.o ./src/Lapack/Blas/saxpy.o ./src/Lapack/Blas/scopy.o ./src/Lapack/Blas/sdot.o ./src/Lapack/Blas/sgemm.o ./src/Lapack/Blas/sgemv.o ./src/Lapack/Blas/sger.o ./src/Lapack/Blas/snrm2.o ./src/Lapack/Blas/srot.o ./src/Lapack/Blas/sscal.o ./src/Lapack/Blas/sswap.o ./src/Lapack/Blas/strmm.o ./src/Lapack/Blas/strmv.o ./src/Lapack/Blas/strsm.o ./src/Lapack/Blas/xerbla.o ./src/main.o -lm
Finished building target: EmbeddedLapack
13:15:54 Build Finished. 0 errors, 0 warnings. (took 563ms)
-------------------------------------------------------------------------------------------------
#include <time.h>
#include "LinearAlgebra/declareFunctions.h"
int main() {
/*
* y = measured output values
* u = measured input values
*/
clock_t start, end;
float cpu_time_used;
start = clock();
double y[144] = { 0.00000, 0.49525, 1.43863, 2.13779, 2.30516, 2.05713,
1.69220, 1.45608, 1.42777, 1.54146, 1.67927, 1.75624, 1.75400,
1.70478, 1.65394, 1.62996, 1.63549, 1.65594, 1.67426, 1.68125,
1.67752, 1.66930, 1.66285, 1.66102, 1.66300, 1.66621, 1.66842,
1.66880, 1.66786, 1.66664, 1.66591, 1.66588, 1.66629, 1.66675,
1.66698, 1.66695, 1.66678, 1.66661, 1.66654, 1.66657, 1.66664,
1.66670, 1.66672, 1.66670, 1.66667, 1.66665, 1.66665, 1.66666,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66666, 1.66666,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667 };
double u[144] = { 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5 };
// Toeplitz matrix
double toe[144 * 144];
toeplitz(u, toe, 144);
// Upper triangular
double tru[144 * 144];
triu(toe, tru, 0, 144, 144);
// inverse
inv(tru, 144);
// Multiplication
double g[144];
mul(y, tru, false, g, 1, 144, 144);
// Create hankel
double H0[144 * 144];
hankel(g, H0, 144, 1);
double H1[144 * 144];
hankel(g, H1, 144, 2);
// Cut hankel into half
double H0_half[72 * 72];
double H1_half[72 * 72];
cut(H0, 144, 144, H0_half, 0, 71, 0, 71);
cut(H1, 144, 144, H1_half, 0, 71, 0, 71);
// Do SVD
double U[72 * 72];
double S[72 * 72];
double V[72 * 72];
svd(H0_half, U, S, V, 72, 72);
/*
* Collect all singular values
*/
double B[72*1];
mdiag(S, B, 72, 72);
print(B, 72, 1);
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
-----------------------------------------------------------------------------------------
0.407681034422245847
0.238123608303610790
0.000011845213482911
0.000011666082457162
0.000008883438909084
0.000008631689698976
0.000007734962524526
0.000007511490842174
0.000007488406152694
0.000007407380025140
0.000006121475748177
0.000005522531730072
0.000005116007541059
0.000004797631110215
0.000004784509561686
0.000004473545605918
0.000004342577631107
0.000004064797343488
0.000004063644188412
0.000003865877590879
0.000003653037790875
0.000003637842419990
0.000003386516594547
0.000003130366457631
0.000002977246663017
0.000002882530710919
0.000002538497184049
0.000002505827486202
0.000002309697235112
0.000001808839531249
0.000001797106897059
0.000001565211931281
0.000001555312183134
0.000001408267510825
0.000001365907202482
0.000001302339916052
0.000001237594241464
0.000001108041144894
0.000001061571017183
0.000000937397714155
0.000000871167733055
0.000000834535321843
0.000000760280816693
0.000000676935925759
0.000000657762114094
0.000000612476643054
0.000000541625110851
0.000000514281053563
0.000000439069844454
0.000000370412162418
0.000000023499011157
0.000000018764254299
0.000000001444867446
0.000000001262488202
0.000000000836084418
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
0.000000000000000000
Total speed was 0.005488,
13:11:58 **** Incremental Build of configuration Debug for project TestSVD ****
make all
Building file: ../src/TestSVD.cpp
Invoking: Cross G++ Compiler
g++ -O2 -g3 -Wall -c -fmessage-length=0 -MMD -MP -MF"src/TestSVD.d" -MT"src/TestSVD.o" -o "src/TestSVD.o" "../src/TestSVD.cpp"
Finished building: ../src/TestSVD.cpp
Building target: TestSVD
Invoking: Cross G++ Linker
g++ -o "TestSVD" ./src/TestSVD.o -larmadillo
Finished building target: TestSVD
13:12:04 Build Finished. 0 errors, 0 warnings. (took 6s.452ms)
------------------------------------------------------------------------------
/*
* Simulation with Armadillo C++
*/
#include <iostream>
#include <armadillo>
#include <time.h>
using namespace std;
using namespace arma;
int main() {
clock_t start, end;
float cpu_time_used;
start = clock();
/*
* Declare vector and matrix
*/
mat u(1, 144);
mat y(1, 144);
mat toe(144, 144);
mat triup(144, 144);
mat inverse(144, 144);
mat g(1, 144); // markov parameters
vec g_v; // Impulse vector
mat H1(144, 144); // Hankel 1 of markov parameters
mat H1_half(72, 72);
/*
* Step singal
*/
double output[144] = { 0.00000, 0.49525, 1.43863, 2.13779, 2.30516, 2.05713,
1.69220, 1.45608, 1.42777, 1.54146, 1.67927, 1.75624, 1.75400,
1.70478, 1.65394, 1.62996, 1.63549, 1.65594, 1.67426, 1.68125,
1.67752, 1.66930, 1.66285, 1.66102, 1.66300, 1.66621, 1.66842,
1.66880, 1.66786, 1.66664, 1.66591, 1.66588, 1.66629, 1.66675,
1.66698, 1.66695, 1.66678, 1.66661, 1.66654, 1.66657, 1.66664,
1.66670, 1.66672, 1.66670, 1.66667, 1.66665, 1.66665, 1.66666,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66666, 1.66666,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667, 1.66667,
1.66667, 1.66667, 1.66667, 1.66667, 1.66667 };
double input[144] = { 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5 };
// Insert
for (int i = 0; i < 144; i++) {
u(0, i) = input[i];
y(0, i) = output[i];
}
// Toeplitz
toe = toeplitz(u);
// Triangular upper
triup = trimatu(toe);
// inverse
inverse = inv(triup);
// impulse
g = y * inverse;
// Turn it to a vector
g_v = trans(g);
// Create a initial matrix
int length = g_v.n_rows;
for (int i = 0; i < length; i++) {
for (int j = 0; j < length; j++) {
if (j + i + 1 >= length) {
H1(i, j) = 0;
} else {
H1(i, j) = g_v(j + i + 1);
}
}
}
// cut
H1_half = H1(span(0, 71), span(0, 71));
mat U;
vec s;
mat V;
svd(U, s, V, H1_half);
s.print("s-matrix: ");
end = clock();
cpu_time_used = ((float) (end - start)) / CLOCKS_PER_SEC;
printf("\nTotal speed was %f,", cpu_time_used);
return 0;
}
-------------------------------------------------------------------------------------
s-matrix:
4.0768e-01
2.3812e-01
1.1845e-05
1.1666e-05
8.8834e-06
8.6317e-06
7.7350e-06
7.5115e-06
7.4884e-06
7.4074e-06
6.1215e-06
5.5225e-06
5.1160e-06
4.7976e-06
4.7845e-06
4.4735e-06
4.3426e-06
4.0648e-06
4.0636e-06
3.8659e-06
3.6530e-06
3.6378e-06
3.3865e-06
3.1304e-06
2.9772e-06
2.8825e-06
2.5385e-06
2.5058e-06
2.3097e-06
1.8088e-06
1.7971e-06
1.5652e-06
1.5553e-06
1.4083e-06
1.3659e-06
1.3023e-06
1.2376e-06
1.1080e-06
1.0616e-06
9.3740e-07
8.7117e-07
8.3454e-07
7.6028e-07
6.7694e-07
6.5776e-07
6.1248e-07
5.4163e-07
5.1428e-07
4.3907e-07
3.7041e-07
2.3499e-08
1.8764e-08
1.4449e-09
1.2625e-09
8.3608e-10
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
2.7890e-17
Total speed was 0.031486,
function simu()
tic
% Input signals
y = [0.000000000000000000
0.495250000000000024
1.438630000000000075
2.137789999999999857
2.305159999999999876
2.057129999999999903
1.692199999999999926
1.456080000000000041
1.427769999999999984
1.541460000000000052
1.679270000000000040
1.756240000000000023
1.754000000000000004
1.704779999999999962
1.653939999999999966
1.629960000000000075
1.635490000000000110
1.655939999999999968
1.674260000000000081
1.681249999999999911
1.677519999999999900
1.669300000000000006
1.662849999999999939
1.661019999999999941
1.663000000000000034
1.666209999999999969
1.668420000000000014
1.668800000000000061
1.667859999999999898
1.666639999999999899
1.665910000000000002
1.665880000000000027
1.666290000000000049
1.666749999999999954
1.666979999999999906
1.666949999999999932
1.666779999999999928
1.666609999999999925
1.666539999999999910
1.666570000000000107
1.666639999999999899
1.666700000000000070
1.666719999999999979
1.666700000000000070
1.666670000000000096
1.666649999999999965
1.666649999999999965
1.666660000000000030
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666660000000000030
1.666660000000000030
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096
1.666670000000000096];
% Output signals
u = linspace(5,5, 144);
% Find impulse response
g = y'*pinv(triu(toeplitz(u)));
% Create hankel matricies
H0 = hank(g, 1);
% SVD
[U,S,V] = svd(H0);
diag(S)
toc
end
% Create the hankel matrix
function [H] = hank(g, k)
H = hankel(g)(1:length(g)/2,1+k:length(g)/2+k);
endfunction
-----------------------------------------------------------------------------------------
>> simu
ans =
4.0768e-01
2.3812e-01
1.1845e-05
1.1666e-05
8.8834e-06
8.6317e-06
7.7350e-06
7.5115e-06
7.4884e-06
7.4074e-06
6.1215e-06
5.5225e-06
5.1160e-06
4.7976e-06
4.7845e-06
4.4735e-06
4.3426e-06
4.0648e-06
4.0636e-06
3.8659e-06
3.6530e-06
3.6378e-06
3.3865e-06
3.1304e-06
2.9772e-06
2.8825e-06
2.5385e-06
2.5058e-06
2.3097e-06
1.8088e-06
1.7971e-06
1.5652e-06
1.5553e-06
1.4083e-06
1.3659e-06
1.3023e-06
1.2376e-06
1.1080e-06
1.0616e-06
9.3740e-07
8.7117e-07
8.3454e-07
7.6028e-07
6.7694e-07
6.5776e-07
6.1248e-07
5.4163e-07
5.1428e-07
4.3907e-07
3.7041e-07
2.3499e-08
1.8764e-08
1.4449e-09
1.2625e-09
8.3608e-10
3.9554e-15
3.5735e-15
3.2392e-15
3.0822e-15
2.8466e-15
2.8323e-15
2.4565e-15
1.6915e-15
1.5164e-15
1.2658e-15
1.0899e-15
1.0884e-15
7.1103e-16
5.1639e-16
4.4834e-16
3.3557e-16
1.8073e-16
Elapsed time is 0.038156 seconds.
>>
EmbeddedLapack is about 6 times faster than Armadillo in this case and EmbeddedLapack is about 7 times faster than GNU Octave
>> 0.031486/0.005488
ans = 5.7372
>> 0.038156/0.005488
ans = 6.9526
If you don't know how to use the function, you can read the .c file of that function that you want to use. It will always be a comment above the function name that describe what you should have as argument, what size and what data type and what it will return. Here is an example.
#include "declareFunctions.h"
/*
* Cut a matrix A with size row x columns into a matrix B with size (stop_row - start_row + 1) x (stop_column - start_column + 1).
* Remember! Indexing start and stop are from zero!
*
* Example:
* If you have a matrix A 5 x 6 and you want to cut the values from A to matrix B with size 3 x 3 and you want to start at 0,0 and end at 3,3
* Code: cut(A, 5, 6, B, 0, 2, 0, 2); // Because indexing from zero
*/
void cut(double* A, int row, int column, double* B, int start_row, int stop_row, int start_column, int stop_column) {
int in_columns = column;
double* data = A + start_row * in_columns + start_column;
// Create the output
//double* ptr = B;
int out_columns = stop_column - start_column + 1;
// Instead of having two for loops, we just copy the whole row at once.
for (int i = start_row; i < stop_row + 1; i++) {
memcpy(B, data, sizeof(double) * out_columns);
B += out_columns;
data += in_columns;
}
}
Download the clapack.tgz file above, or from here http://www.netlib.org/clapack/. Extract it. Then you can copy and paste the files into the subfolders of folder "Lapack" from the EmbeddedLapack -> src folder, so you can have your desire Lapack subroutine to work. You can see how I have done. Just do the same. I just include the Lapack routine I want to use, and then I got lots of errors in the compiling and those errors asking for functions from other .c files located from clapack.tgz file. I copy and paste functions until all errors where gone.