In statistics, canonical-correlation analysis (CCA) is a way of inferring information from cross-covariance matrices. If we have two vectors X = (X_1, ..., X_n) and Y = (Y_1, ..., Y_m) of random variables, and there are correlations among the variables, then canonical-correlation analysis will find linear combinations of the X_i and Y_j which have maximum correlation with each other.
This repository contains a group of study material of CCA related algorithm.
The Notebook contains topics:
- CCA: Implementation in Numpy
- KCCA
- DCCA
- DCCAE
- VCCA: Derivation of the variational lower bound
- VCCA-P
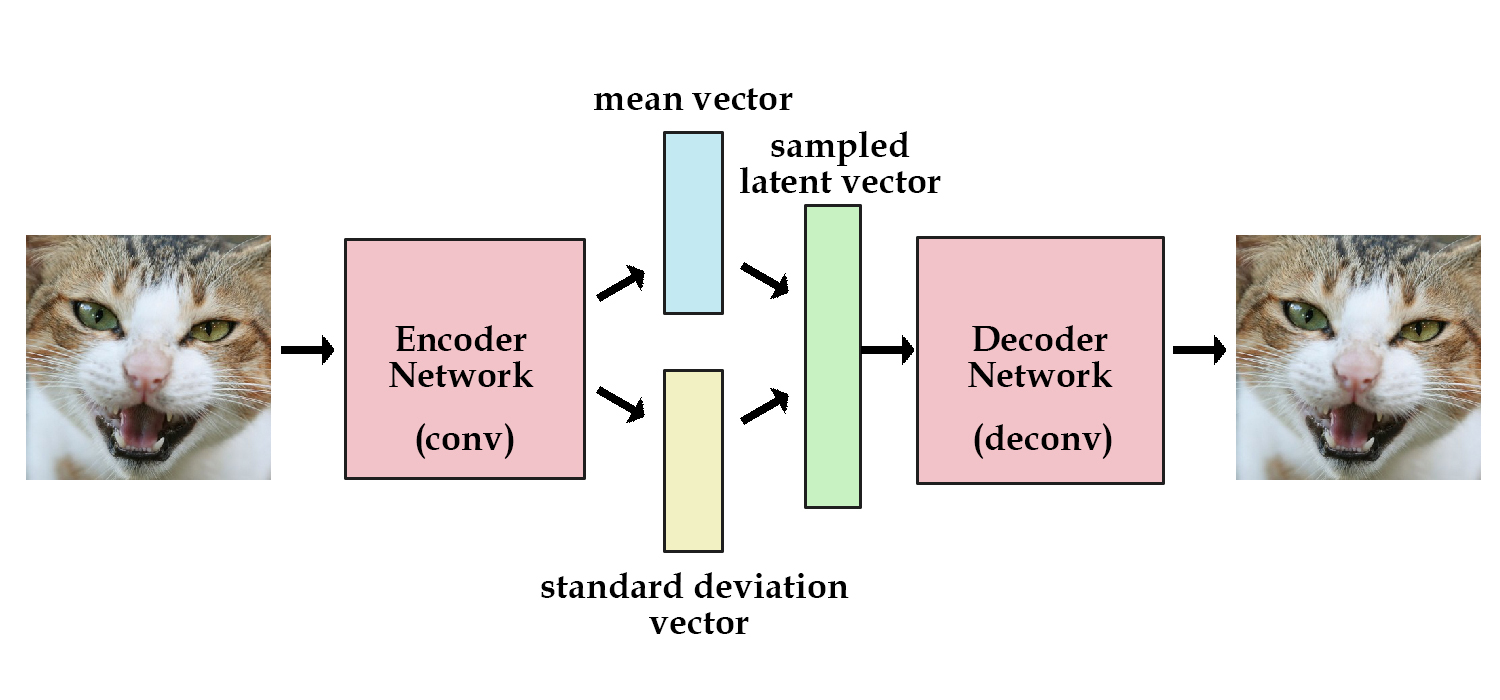
- VAE: ELBO derivation
- CTC
CCA slides 1 CCA slides 2 CCA notes
Multi-view clustering via canonical correlation analysis
Canonical Correlation Analysis: An Overview with application to learning methods
Deep Canonical Correlation Analysis
On Deep Multi-View Representation learning DCCAE
Deep Variational Canonical Correlation Analysis
Acoustic Feature Learning via Deep Variational Canonical Correlation Analysis
[Tutorial on Variational Autoencoders](https://github.com/edchengg/VCCA-StudyNotes/blob/master/paper/VAE.pdf)NIPS 2016 Tutorial: Generative Adversarial Networks
CTC slides 60/100
50/100