Very Fast Simulated Anneling (VFSA)
The image above is a schematic representation of a zero offset Common Reflection Surface (CRS) (in green). This is a traveltime approximation used to approximate the reflection data (in blue) in the neighborhood of a central Common Mid Point (CMP) P0. This approximation surface is determined by 3 parameters (RN, RNIP, and BETA) associated with a normal ray (in red) and with a CMP location in the acquisition surface (P0 point).
The Very Fast Simulated Annealing (VFSA) algorithm optimizes the global search of these CRS parameters. It uses the semblance between a CRS approximation surface and the reflection surface in the seismic data as a convergence criterion. The main assumption of this algorithm is that the CRS parameters that produce the best fit between these surfaces will be the optimized ones.
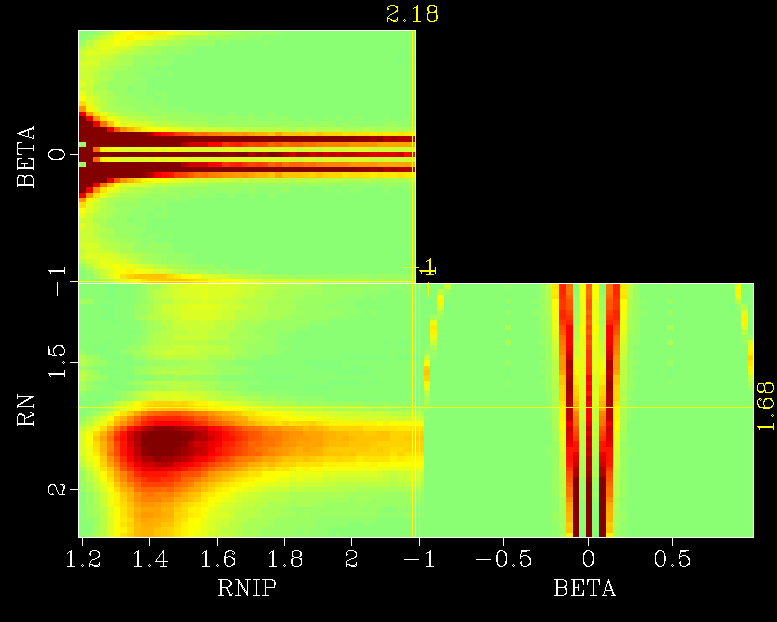
In the image bellow we have the semblance between an approximation surface and a reflection seismic data in function of RN, RNIP and BETA parameters. The values in red are the major values of the semblance function (it varies from 0 to 1). We can see a red region with the best semblance values for a set of the parameters. The purpose of the VFSA algorithm is to find these region precisely and faster ("faster" mean as quick as possible with less computational effort).
The concept of Simulated Annealing (SA) methods is to find the optimal (minimum or maximum) of an energy function E(m) for a set of model parameters values m. These algorithms simulate a physical system that slowly evolves to a state (each configuration of the particles) of minimum energy. The description of the annealing process (Sen and Stoffa, 1995):
"A physical annealing process occurs when a solid in a heat bath is initially
heated by increasing the temperature such that all the particles
are distributed randomly in a liquid phase. This is followed by
slow cooling such that all the particles arrange themselves in the low energy
ground state where crystallization occurs."
We adapt the VFSA algorithm to be used in zero-offset Common Reflection Surface (CRS) parameters optimization. The error function E(m) is the Semblance function between a CRS traveltime approximation and the seismic data. Because the CRS traveltime approximation is a function of the model parameters, m={RN,RNIP,BETA}, the model parameters that produce the best fit will be the optimized ones.
"In optimization problems such as those that occur in geophysical inverse problems,
the energy function is defined with the error function
E(m). The error is a function of the possible geophysical models and takes
on different configurations or models. We are interested in
finding the state (or model) m for which this error is minimum.
Simulated Annealing (SA) is implemented using a computer algorithm
that mimics the physical annealing process to find the global
minimum energy state." (Sen and Stoffa, 1995)
ALGORITHM: A pseudo code of the Very Fast Simulated Annealing (VFSA) algorithm.
INPUT: Arbitrary initial value of parameters vector m=m0 in a search window. Initial temperature T0.
OUTPUT: Optimized parameters opt={m1,m2,...,mi,...,mN}.
LOOP {Annealing of the temperature T0 em q iterations}
| {Obtain temperature Tq of the q iteration for M parameters}
| Tq = T0 * exp(−C0 * q^(M −1));
| LOOP {Update each model parameter mi = 1, ..., M}
| | {Obtain a random number ui}
| | ui ∈ U [0, 1]
| | {Obtain parameter pertubation yi}
| | yi = sgn(ui − 12 )Ti ′ [(1 + Ti ′)2ui −1 − 1];
| | {Distub parameter inside the search window}
| | mnew = mold + yi (mmax − mmin);
| | mmin <= mnew ≤ mmax;
| END LOOP
| {Calculate energy function for new parameters (mnew)}
| ΔE = E(mnew) − E(m0);
| IF E(mnew) > E(m0) THEN
| | {Keep current parameters (mnew)}
| | opt = mnew
| END IF
| {Update parameters using using Metropolis criteria}
| P = exp(−ΔE/T)
| IF ΔE ≤ 0 THEN
| | {Update parameters}
| | m0 = mnew ;
| | E(m0) = E(mnew);
| END IF
| IF ΔE > 0 THEN
| | {Write a random number}
| | r = U [0, 1];
| | IF P > r THEN
| | | {Update parameters}
| | | m0 = mnew;
| | | E(m0) = E(mnew);
| | END IF
| END IF
END LOOP
The input parameters T0 (initial temperature) and C0 (damping factor) are control parameters to tune the algorithm for specific problems, and they are chosen arbitrarily. The mmin and mmax are values to define the parameters search window and they should be specified for each model parameter.
For more details, please refer to:
- Global optimization methods in geophysical inversion, M. Sen, P.L. Stoffa, 1995.
- Non-hyperbolic common reflection surface, S. Fomel, R. Kazinnik, 2013 available in Madagascar reproducible documents: Non-hyperbolic common reflection surface