BinPy

• About
• Installation
• Available Resources
• Documentation
• Contribute

What is BinPy?

It is a library which will serve as a base to develop circuit based applications and educational software on top of it. BinPy is a clear representation of fundamentals. Everything has been written from scratch such as gates, logical operations, etc. This package does not depend on any external library other than pure Python. It aims to extend the hardware programming concepts to Python.

How to use

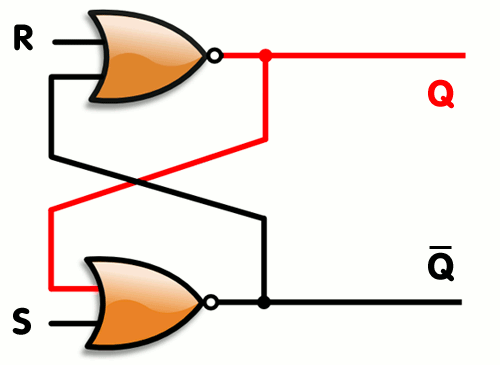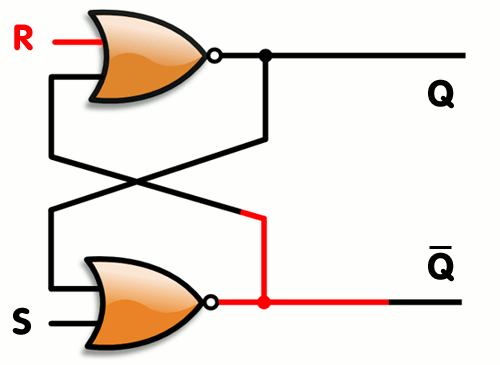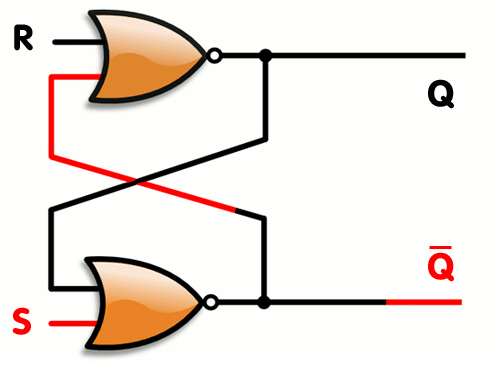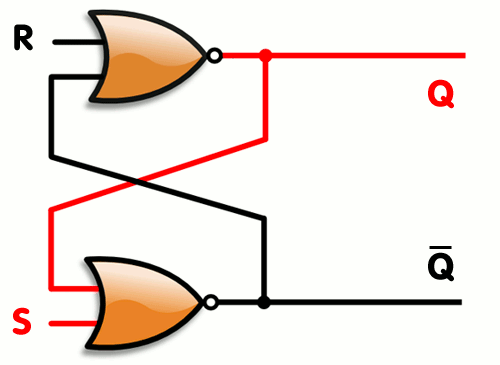
Here's an example of SR latch constructed from a pair of cross-coupled NOR gates

from BinPy import *

a = Connector()
b = Connector()

g1 = NOR(R,b)
g1.setOutput(a)    # SET OUTPUT as a

g2 = NOR(S,a) 
g2.setOutput(b)    # SET OUTPUT as b

print [g1.output(),g2.output]

Output

Q:  True 	Q':  False
Q:  False 	Q':  True
Q:  False 	Q':  True
Q:  False 	Q':  False	#Invalid State

Operations, Combinatonal Logic and Algorithms

from BinPy import *

#Operations
operator = Operations()
operator.ADD(1011,11)
operator.SUB(1011,11)
operator.COMP('0011',1) #Second argument chooses betweem 1's or 2's Compliment


#Combinational Logic
d = Decoder([1,1,0,1])
print "Decoder Out: ", d.output('01')

#Sequential Circuits
a = DFlipFlop(1,0)
print "DFlipFlop Out: ", a.output()

#IC
myIC = IC_7400()
p = {1:1,2:0,4:0,5:0,7:0,10:1,9:1,13:0,12:0,14:1}
myIC.setIC(p)
print "IC_7400 Out: ", myIC.run()

myIC1 = IC_7401()
p = {2:0,3:1,5:0,6:0,7:0,8:1,9:1,11:0,12:0,14:1}
myIC1.setIC(p)
print "IC_7401 Out: ", myIC1.run()

#Algorithms 
#Includes the Quine-McCluskey algorithm for solving K-Maps
FinalEquation = QM(['A','B'])
print "Minimized Boolean Equation : " , FinalEquation.get_function(qm.solve([0,1,2],[])[1])

Output

{'carry': 0, 'sum': [1, 1, 1, 0]}
{'carry': 1, 'difference': [1, 0, 0, 0]}
Decoder Out:  1
DFlipFlop Out: [1,0]
IC_7400 Out:  {8: 0, 11: 1, 3: 1, 6: 1}
IC_7401 Out:  {1: 1, 10: 0, 4: 1, 13: 1}
Minimized Boolean Equation : ((NOT B) OR (NOT A))

Available Resources

• All basic logic gates (NOT, OR, NOR, AND, NAND, XOR, XNOR)

• Combinational logics

  • Adder
  • Subtractor
  • Multiplier
  • MUX (2:1, 4:1, 8:1, 16:1)
  • DEMUX (1:2, 1:4, 1:8, 1:16)
  • Encoder

• IC

  • 7400
  • 7401
  • 7402
  • 7403
  • 7404
  • 7405
  • 7408
  • 7410
  • 7411
  • 7412
  • 7413
  • 7415
  • 7416
  • 7417
  • 7418
  • 7419
  • 7420
  • 7421
  • 7422
  • 7424
  • 7425
  • 7426
  • 7427
  • 7428
  • 7430
  • 7432
  • 7433
  • 7437
  • 7440
  • 7451
  • 7454
  • 7455
  • 7458
  • 7464
  • 7486
  • 741G00
  • 741G02
  • 741G03
  • 741G04
  • 741G05
  • 741G08
  • 7431
  • 7442
  • 7443
  • 7444
  • 7445
  • 74133
  • 74260

• Algorithms

  • Quine-McCluskey Algorithm (To find minimized Boolean Equation)
  • Moore Machine Optimizer

Documentation

Auto-generated documentation is available for reference at BinPy docs

Installation

Linux

Install with pip

sudo apt-get install pip setuptools ipython
sudo pip install https://github.com/BinPy/BinPy/zipball/master

Install using git

sudo apt-get install git setuptools ipython
git clone https://github.com/BinPy/BinPy.git
cd BinPy/
sudo python setup.py install

Future Work

• Introduction of all ICs
• Introduction of problem solving algorithms
• Addition of Microprocessors and Analog Devices
• Graphical representation of the circuit
• ...

How To Contribute

• Report Bugs and Issues
• Solve Bugs and Issues
• Write Tutorials, Examples and Documentation