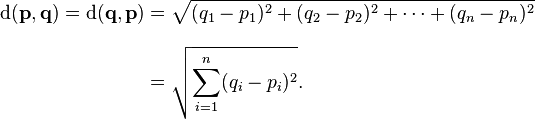K-Means kümeleme mantığını kavrayabilmemiz için öncelikle kümelemenin tanımını yapmamız gerekir.
Kümeleme analizi, bir veri kümesindeki bilgileri belirli yakınlık kriterlerine göre gruplara ayırma işlemidir.
Bu grupların her birine küme denir. Kümeleme ise en basit tanımıyla
benzer özellik gösteren veri elemanlarının kendi aralarında gruplara ayrılmasıdır. [1]
Aynı küme içindeki elemanların benzerliği fazla, kümeler arası benzerlik ise az olmalıdır. Bu tanımlara göre her küme temsil ettiği nesneleri en iyi ifade edecek şekilde düzenlenir.
Burada temel amaç , yeni gelecek ve henüz hangi sınıfta olduğu bilinmeyen verilerin var olan sınıflardan en uygun olanına yerleştirilmesidir.
Kümeleme analizi istatistik, biyoloji, uzaysal veri madenciliği ve makine öğrenmesi, örüntü tanıma ve resim tanıma alanlarında kullanılmaktadır. İstatistik dünyasında k-means ve k-medoids kümeleme yöntemlerini kullanan S-Plus, SPSS ve SAS gibi paket programlar yoğunlukla kullanılmaktadır. Biyolojide genetik yapıların sınıflandırılması ve yeni yapıların keşfinde, uzaysal/düzlemsel veri madenciliğinde coğrafi konuma göre yerleşim yerlerine götürülecek mal ve hizmetler için ideal yer belirlemede, yapay zekâ alanında makine öğrenmesi için gözetimsiz öğrenme metodu olarak kullanılmaktadır.
En eski kümeleme yöntemlerinden biri olan k-means 1957 yılında ilk kez Hugo Steinhaus’un öne sürdüğü bir fikir olmasına rağmen 1967 yılında J.B. MacQueen tarafından geliştirilmiştir. K-means algoritmasının genel mantığı n adet veri nesnesinden oluşan bir veri setini, giriş parametresi olarak verilen k adet kümeye bölümlemektir. Amaç, gerçekleştirilen bölümleme işlemi sonunda elde edilen kümelerin, küme içi benzerliklerinin maksimum ve kümeler arası benzerliklerinin minimum olmasını sağlamaktır. Küme benzerliği, kümenin ağırlık merkezi olarak kabul edilen bir nesne ile kümedeki diğer nesneler arasındaki uzaklıkların ortalama değeri ile ölçülmektedir.
Algoritmaya k-means adı verilmesinin nedeni, algoritmanın çalışmasından önce sabit bir küme sayısına
ihtiyaç duyulmasıdır. Küme sayısı 'k' ile gösterilir ve elemanlarının birbirlerine olan yakınlıklarına
göre oluşacak grup sayısını ifade eder. Buna göre 'k' önceden bilinen ve kümeleme işlemi bitene kadar
değeri değişmeyen sabit bir pozitif tam sayıdır.
K-Means Algoritmasının Matematiği
K-Means algoritmasında verilerin merkeze olan uzaklıklarının hesaplanmasında öklid uzaklık formülü temel alınmıştır.
Öklid Uzaklığı
Öklid uzaklık formülü en yaygın olarak kullanılan uzaklık hesaplama formülüdür. Burada kullanılan p ve q iki nesnedir. d(p,q) ise iki nesne arasında ki uzaklığı veri. [2]
K-Means Algoritmasının İşlem Basamakları
İlk olarak küme merkezleri belirlenir. Belirleme işlemi yapılırken iki yol izlenilebilir:
- Küme merkezleri rastgele bir nokta veya noktalar kümesi seçilebilir.
- Küme merkezleri kullanılacak olan veri setinden seçilebilir.
Veri setindeki her bir noktanın merkezlere olan uzaklıkları öklid formülü ile hesaplanır ve karşılaştırılır. Noktalar en yakın oldukları merkezin kümesine dahil edilir.
Oluşan yeni kümelerin ağırlık merkezleri (ortalama değerleri) hesaplanır. Hesaplanan bu değerler kümelerin yeni merkezleridir. Veri setindeki her bir noktanın yeni merkezlere olan uzaklıkları tekrar hesaplanır.
Küme merkezlerinin yer değiştirmelerinden dolayı kümeler içerisindeki verilerin de küme değiştirmesi söz konusudur. Dolayısıyla tam anlamıyla kümeleme işlemi yapılabilmesi için kümeler kararlı hale gelene kadar 2. ve 3. adımların tekrarlanması gerekir.
NOT Kümelerin kararlı yapıya geçmesinde birkaç yaklaşım söz konusudur. Bunlardan biri, hesaplanan merkezlerin koordinatlarının bir sonraki döngüde hesaplanan merkezlerin koordinatlarıyla eşit olmasıdır. Aşağıda paylaştığımız algoritma ve kod örneğinde de bu yaklaşım kullanılmıştır.
Fakat bu yaklaşımda farklı iki nokta çiftlerinin de aynı merkezi verebilme ihtimali göz ardı edilmemelidir.
Diğer bir yaklaşım ise, belirli adımlar sonucu oluşan kümelerdeki elemanların, bir sonraki döngü sonucunda oluşan kümelerdeki elemanlarla aynı kümelerde bulunmasıdır. Bu yaklaşım diğer yaklaşıma göre daha az hata payına sahiptir.
K-Means Akış Diyagramı
Phyton dilinde K-Means Algoritmasının Kodu
import math
### giris degerleri
inputvalue = []
class1 = []
class2 = []
class3 = []
center1 = [5.5,2.6,4.4,1.2]
center2 = [5.8,2.7,5.1,1.9]
center3 = [7.2,3.2,6.0,1.8]
iteration = 100
### verilerin kume merkezlerine olan uzakliklarinin hesaplandigi fonksiyon
def distance(centersw,centersl,centerpw,centerpl,value1,value2,value3,value4):
return math.sqrt((centersw-value1)**2 + (centersl-value2)**2 + (centerpw-value3)**2 + (centerpl-value4)**2)
### verilerin merkezlere olan uzakliklarina gore kumelere ayrildigi fonksiyon
def clustering(center1,center2,center3,value1,value2,value3,value4):
wclass1 = distance(center1[0],center1[1],center1[2],center1[3],value1,value2,value3,value4)
wclass2 = distance(center2[0],center2[1],center2[2],center2[3],value1,value2,value3,value4)
wclass3 = distance(center3[0],center3[1],center3[2],center3[3],value1,value2,value3,value4)
value = [value1,value2,value3,value4]
if wclass1 < wclass2 and wclass1 < wclass3 :
class1.append(value)
elif wclass2 < wclass1 and wclass2 < wclass3 :
class2.append(value)
elif wclass3 < wclass2 and wclass3 < wclass1 :
class3.append(value)
### olusturulan yeni kumelerdeki verilere gore yeni merkezlerin bulundugu fonksiyon
def new_center(classvalue):
x = 0.0
y = 0.0
z = 0.0
t = 0.0
for i in range(len(classvalue)):
x += classvalue[i][0]
y += classvalue[i][1]
z += classvalue[i][2]
t += classvalue[i][3]
return [x/len(classvalue),y/len(classvalue),z/len(classvalue),t/len(classvalue)]
### iris_data dosyasindan verilerin okundugu kod parcasi
with open('iris_data.txt') as openfile:
for line in openfile:
inputvalue.append(line.split(","))
### dosyadaki verilerden kullanilacak olanlarin inputvalue listesine yazildigi kod parcasi
for i in range(len(inputvalue)):
for j in range(len(inputvalue[i])):
if j == 0 or j % 4 != 0 :
inputvalue[i][j] = float(inputvalue[i][j])
else:
continue
### merkezler yedeklenir, daha sonra kumeleme fonksiyonuyla yeni merkezler hesaplanir.
for i in range(iteration):
backup_center1 = center1
backup_center2 = center2
backup_center3 = center3
for i in range(len(inputvalue)):
clustering(center1,center2,center3, inputvalue[i][0],inputvalue[i][1],inputvalue[i][2],inputvalue[i][3])
center1 = new_center(class1)
center2 = new_center(class2)
center3 = new_center(class3)
### Verilen veri setindeki kumelerin gercekten ayni verilerden olusup olusmadigini kontrol eden kod parcasi
i1 = 0
i2 = 0
i3 = 0
for i in range(3):
count1 = 0
count2 = 0
count3 = 0
for j in range(i*50,(i+1)*50):
if i1 < len(class1) and class1[i1]==inputvalue[j]:
count1+=1
i1 += 1
elif i2 < len(class2) and class2[i2]==inputvalue[j]:
count2+=1
i2 += 1
elif i3 < len(class3) and class3[i3]==inputvalue[j]:
count3+=1
i3 += 1
print count1,count2,count3,j
### yeni kumeler ve merkezler yazdirilir daha sonra kumeler tekrar bosaltilir
print "****************"
print len(class1),len(class2),len(class3)
center1 = new_center(class1)
center2 = new_center(class2)
center3 = new_center(class3)
print center1
print center2
print center3
class1 = []
class2 = []
class3 = []
### yedeklenen merkez koordinatlari ile yeni merkez koordinatlari ayni olana kadar bu dongu devam eder.
if backup_center1[0]-center1[0]==0 and backup_center1[1]-center1[1]==0 and \
backup_center2[0]-center2[0]==0 and backup_center2[1]-center2[1]==0 and \
backup_center3[0]-center3[0]==0 and backup_center3[1]-center3[1]==0:
break
else:
continue