Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Sibling PR of introduction of Setfield.jl in AbstractPPL.jl (#295)
This is a sibling PR to TuringLang/AbstractPPL.jl#26 fixing some issues + allowing us to do neat stuff. We also finally drop the passing of the `inds` around in the tilde-pipeline, which is not very useful now that we have the more general lenses in `VarName`. TODOs: - [X] ~Deprecate `*tilde_*` with `inds` argument appropriately.~ EDIT: On second thought, let's not. See comment for reason. - [x] It seems like the prob macro is now somehow broken 😕 - [X] ~(Maybe) Rewrite `@model` to not escape the entire expression.~ Deferred to #311 - [X] Figure out performance degradation. - Answer: `hash` for `Tuple` vs. `hash` for immutable struct 😕 ## Sample fields of structs ```julia julia> @model function demo(x, y) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 2:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end # Dynamic indexing x.a[begin] ~ Normal(-100.0, 1.0) x.a[end] ~ Normal(100.0, 1.0) # Immutable set y.a ~ Normal() # Dotted z = Vector{Float64}(undef, 3) z[1:2] .~ Normal() z[end:end] .~ Normal() return (; s, m, x, y, z) end julia> struct MyCoolStruct{T} a::T end julia> m = demo(MyCoolStruct([missing, missing]), MyCoolStruct(missing)); julia> m() (s = 3.483799020996254, m = -0.35566330762328, x = MyCoolStruct{Vector{Union{Missing, Float64}}}(Union{Missing, Float64}[-100.75592540694562, 98.61295291877542]), y = MyCoolStruct{Float64}(-2.1107980419121546), z = [-2.2868359094832584, -1.1378866583607443, 1.172250491861777]) ``` ## Sample fields of `DataFrame` ```julia julia> using DataFrames julia> using Setfield: ConstructionBase julia> function ConstructionBase.setproperties(df::DataFrame, patch::NamedTuple) # Only need `copy` because we'll replace entire columns columns = copy(DataFrames._columns(df)) colindex = DataFrames.index(df) for k in keys(patch) columns[colindex[k]] = patch[k] end return DataFrame(columns, colindex) end julia> @model function demo(x) s ~ InverseGamma(2, 3) m ~ Normal(0, √s) for i in 1:length(x.a) - 1 x.a[i] ~ Normal(m, √s) end x.a[end] ~ Normal(100.0, 1.0) return x end demo (generic function with 1 method) julia> m = demo(df, (a = missing, )); julia> m() 3×1 DataFrame Row │ a │ Float64? ─────┼────────── 1 │ 1.0 2 │ 2.0 3 │ 99.8838 julia> df 3×1 DataFrame Row │ a │ Float64? ─────┼─────────── 1 │ 1.0 2 │ 2.0 3 │ missing ``` # Benchmarks Unfortunately there does seem to be performance regression when using a very large number of varnames in a loop in the model (for broadcasting which uses the same number of varnames but does so "internally", there is no difference): 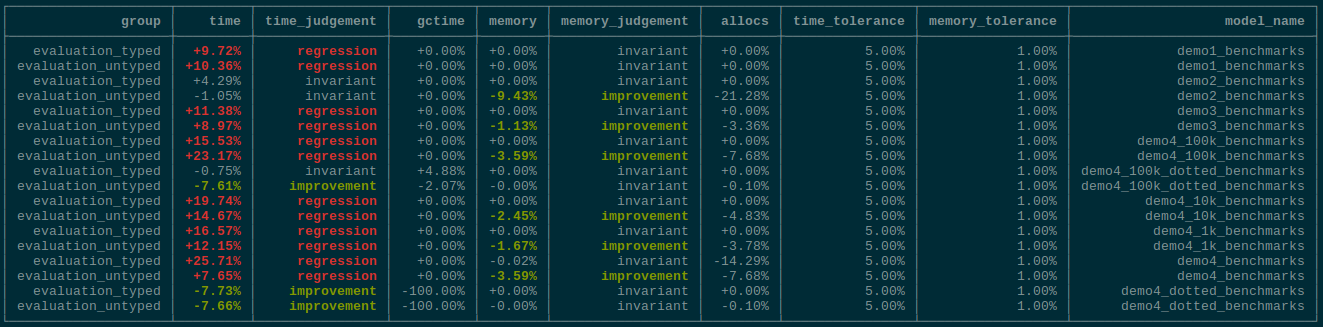 The weird thing is that we're using less memory, indicating that type-inference might better? <details> <summary>0.31.1</summary> ## 0.31.1 ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 0.059594 seconds (115.76 k allocations: 6.982 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 619.000 ns … 19.678 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 654.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 677.650 ns ± 333.145 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅▆▇█▅▄▃ ▃▅███████▇▆▅▄▃▄▄▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃ 619 ns Histogram: frequency by time 945 ns < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 249.000 ns … 11.048 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 264.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 267.650 ns ± 137.452 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▂▄ ▆▇ █▇ ▇▄ ▂▂ ▂▂▂▁▂▂▁▃▃▁▅▅▁███▁██▁██▁██▁██▁▇▇▅▁▄▄▁▃▃▁▃▃▁▃▂▁▂▂▂▁▂▂▁▂▂▁▂▂▁▂▂▂ ▃ 249 ns Histogram: frequency by time 291 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.067078 seconds (143.91 k allocations: 8.544 MiB, 99.91% compilation tim e) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.637 μs … 48.917 μs ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.694 μs ┊ GC (median): 0.00% Time (mean ± σ): 1.746 μs ± 550.372 ns ┊ GC (mean ± σ): 0.00% ± 0.00% ▂█▇▃ ▁▄████▇▄▄▅▅▅▄▃▃▃▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 1.64 μs Histogram: frequency by time 2.23 μs < Memory estimate: 1.66 KiB, allocs estimate: 47. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 506.000 ns … 10.733 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 546.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 553.478 ns ± 118.542 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▃█ ▆▅ ▂▃██▇▇██▅▃▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▁▁▁▂▂▁▁▁▁▁▂▂▁▂▂▁▁▂▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃ 506 ns Histogram: frequency by time 933 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 0.097628 seconds (224.06 k allocations: 13.410 MiB, 99.79% compilation ti me) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 48.200 μs … 16.129 ms ┊ GC (min … max): 0.00% … 99.5 3% Time (median): 51.017 μs ┊ GC (median): 0.00% Time (mean ± σ): 60.128 μs ± 265.008 μs ┊ GC (mean ± σ): 7.61% ± 1.7 2% ▂▆█ ████▂▂▂▁▂▃▄▅▇▅▃▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂ 48.2 μs Histogram: frequency by time 101 μs < Memory estimate: 48.20 KiB, allocs estimate: 1042. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 22.210 μs … 13.796 ms ┊ GC (min … max): 0.00% … 99.7 0% Time (median): 25.882 μs ┊ GC (median): 0.00% Time (mean ± σ): 27.536 μs ± 137.815 μs ┊ GC (mean ± σ): 5.00% ± 1.0 0% █▇▆▄▂ ▁▇▆▇▆▅▄▂ ▂▂▂▁ ▂ ████████████████████████▆▆▃▅▅▅▅▅▅▁▆▇▆▅▅▅▆▆▅▆▇▇▇▇▆▆▅▆▆▅▅▇█▇█▇ █ 22.2 μs Histogram: log(frequency) by time 51 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: loads of indexing #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.435154 seconds (3.12 M allocations: 192.275 MiB, 8.73% gc time, 1.84% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 62 samples with 1 evaluation. Range (min … max): 61.601 ms … 101.432 ms ┊ GC (min … max): 0.00% … 25.0 2% Time (median): 76.902 ms ┊ GC (median): 0.00% Time (mean ± σ): 77.276 ms ± 11.445 ms ┊ GC (mean ± σ): 6.48% ± 10.7 7% ▂ ▂ █ ▆ ▆▆██▄▄▁▄█▄▁▁▁▁▁▁▆▁█▁█▁▄████▁▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▄▁▁▆▁▁▄▆▄▁▄▁▆▄▁▄ ▁ 61.6 ms Histogram: frequency by time 101 ms < Memory estimate: 44.37 MiB, allocs estimate: 1357727. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 189 samples with 1 evaluation. Range (min … max): 23.796 ms … 40.845 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 24.838 ms ┊ GC (median): 0.00% Time (mean ± σ): 25.162 ms ± 1.434 ms ┊ GC (mean ± σ): 0.00% ± 0.00% ▁ ▂▂▃█▂ ▃▂ ▁ ▃▅█▃▇▅█▇██████▇█████▇▄▅▃▅▆▇█▃▆▃▃▄▅▁▄▁▃▁▆▅▄▁▁▁▃▁▃▄▁▁▃▃▁▁▁▁▃▄ ▃ 23.8 ms Histogram: frequency by time 27.8 ms < Memory estimate: 781.70 KiB, allocs estimate: 6. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.476057 seconds (5.08 M allocations: 375.205 MiB, 5.02% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 112.078 ms … 350.311 ms ┊ GC (min … max): 11.20% … 4. 74% Time (median): 115.686 ms ┊ GC (median): 12.93% Time (mean ± σ): 122.722 ms ± 37.638 ms ┊ GC (mean ± σ): 12.96% ± 2. 85% █▅ ▁ ██▅█▅▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▅ ▁ 112 ms Histogram: log(frequency) by time 350 ms < Memory estimate: 347.71 MiB, allocs estimate: 964550. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 59 samples with 1 evaluation. Range (min … max): 69.420 ms … 407.970 ms ┊ GC (min … max): 12.25% … 6.3 0% Time (median): 71.514 ms ┊ GC (median): 12.41% Time (mean ± σ): 78.481 ms ± 43.867 ms ┊ GC (mean ± σ): 12.80% ± 2.8 4% ▅▂█ █▅ ▇██████▅▅▄▁▅▁▁▁▁▁▁▁▁▁▁▁▁▁▅▁▁▁▄▄▁▁▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁ 69.4 ms Histogram: frequency by time 94.2 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details> <details> <summary>This PR</summary> ## This PR ## ### Setup ### ```julia using BenchmarkTools, DynamicPPL, Distributions, Serialization ``` ```julia import DynamicPPLBenchmarks: time_model_def, make_suite, typed_code, weave_child ``` ### Models ### #### `demo1` #### ```julia @model function demo1(x) m ~ Normal() x ~ Normal(m, 1) return (m = m, x = x) end model_def = demo1; data = 1.0; ``` ```julia @time model_def(data)(); ``` ``` 1.063017 seconds (2.88 M allocations: 180.745 MiB, 4.19% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 48 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 615.000 ns … 13.280 ms ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 650.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 2.037 μs ± 132.793 μs ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▇▅▄▄▃▂▁▁ ▁ ███████████▇▇▇▆▆▆▆▃▄▆▆▅▆▇▆▆▇▆▆▇▆▆▆▆▅▆▆▅▅▅▅▄▄▅▅▃▅▅▃▅▄▅▅▅▅▅▄▅▆▅ █ 615 ns Histogram: log(frequency) by time 1.7 μs < Memory estimate: 480 bytes, allocs estimate: 13. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 272.000 ns … 9.093 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 284.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 310.535 ns ± 156.251 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▅█▆▄▃▃▂▁▁ ▁ ███████████▇▇▆▄▄▃▃▄▅▆▅▆▅▆▆▆▆▆▆▆▇▇▆▆▆▆▆▇▆▆▆▆▇▆▇▇▇▇▆▆▆▆▆▅▆▆▅▄▅▅ █ 272 ns Histogram: log(frequency) by time 643 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo2` #### ```julia @model function demo2(y) # Our prior belief about the probability of heads in a coin. p ~ Beta(1, 1) # The number of observations. N = length(y) for n in 1:N # Heads or tails of a coin are drawn from a Bernoulli distribution. y[n] ~ Bernoulli(p) end end model_def = demo2; data = rand(0:1, 10); ``` ```julia @time model_def(data)(); ``` ``` 0.401535 seconds (863.20 k allocations: 51.771 MiB, 2.88% gc time, 99.90% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000003 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 1.672 μs … 9.849 ms ┊ GC (min … max): 0.00% … 0.00% Time (median): 1.754 μs ┊ GC (median): 0.00% Time (mean ± σ): 2.835 μs ± 98.472 μs ┊ GC (mean ± σ): 0.00% ± 0.00% ▅██▇▆▆▅▄▄▃▂▂▁▁ ▁▁▁ ▁ ▂ ██████████████████▇▇▇▇▇▆▇▆▅▆▄▄▁▄▄▄▆▇██████████▆▆▇▇▇▇▆▇▆▆▆▆ █ 1.67 μs Histogram: log(frequency) by time 3.19 μs < Memory estimate: 1.50 KiB, allocs estimate: 37. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 544.000 ns … 19.704 μs ┊ GC (min … max): 0.00% … 0.0 0% Time (median): 567.000 ns ┊ GC (median): 0.00% Time (mean ± σ): 578.671 ns ± 222.201 ns ┊ GC (mean ± σ): 0.00% ± 0.0 0% ▄█▇▅▂▃ ▃███████▅▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▁▁▁▁▁▂▁▂▁▂▁▁▁▁▁▂▂▂▂▂▂▂▁▂▂▂▂▂ ▃ 544 ns Histogram: frequency by time 888 ns < Memory estimate: 0 bytes, allocs estimate: 0. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo3` #### ```julia @model function demo3(x) D, N = size(x) # Draw the parameters for cluster 1. μ1 ~ Normal() # Draw the parameters for cluster 2. μ2 ~ Normal() μ = [μ1, μ2] # Comment out this line if you instead want to draw the weights. w = [0.5, 0.5] # Draw assignments for each datum and generate it from a multivariate normal. k = Vector{Int}(undef, N) for i in 1:N k[i] ~ Categorical(w) x[:,i] ~ MvNormal([μ[k[i]], μ[k[i]]], 1.) end return k end model_def = demo3 # Construct 30 data points for each cluster. N = 30 # Parameters for each cluster, we assume that each cluster is Gaussian distributed in the example. μs = [-3.5, 0.0] # Construct the data points. data = mapreduce(c -> rand(MvNormal([μs[c], μs[c]], 1.), N), hcat, 1:2); ``` ```julia @time model_def(data)(); ``` ``` 1.031824 seconds (2.34 M allocations: 139.934 MiB, 3.16% gc time, 99.96% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (1 allocation: 32 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 52.509 μs … 9.913 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 53.706 μs ┊ GC (median): 0.00% Time (mean ± σ): 61.948 μs ± 210.490 μs ┊ GC (mean ± σ): 9.84% ± 3.27 % ▂▆██▇▆▅▄▄▃▃▂▂▁▁▁▁ ▁ ▂ █████████████████████▇█▇▇▇█████████▇▇▇▇▅▆▆▅▆▅▅▆▇▅▅▄▅▅▄▄▄▄▂▄▃ █ 52.5 μs Histogram: log(frequency) by time 71.3 μs < Memory estimate: 47.66 KiB, allocs estimate: 1007. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 10000 samples with 1 evaluation. Range (min … max): 25.046 μs … 7.474 ms ┊ GC (min … max): 0.00% … 99.4 0% Time (median): 25.591 μs ┊ GC (median): 0.00% Time (mean ± σ): 29.101 μs ± 105.160 μs ┊ GC (mean ± σ): 6.84% ± 1.9 8% ▇█▆▄▃▂▂▁ ▃▄▂▃▃▂▂▁ ▂ █████████▇█████████▇▆▅▆▆▇▇▇▇▅▆▆▅▃▅▄▃▂▂▃▂▄▄▅▄▄▅▄▅▅▅▆▆▅▅▅▅▆▇▇█ █ 25 μs Histogram: log(frequency) by time 46 μs < Memory estimate: 17.62 KiB, allocs estimate: 183. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` #### `demo4`: lots of univariate random variables #### ```julia @model function demo4(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) for i in eachindex(x) x[i] ~ Normal(m, 1.0) end end model_def = demo4 data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 0.835503 seconds (3.93 M allocations: 244.654 MiB, 10.38% gc time, 9.43% compilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000004 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 60 samples with 1 evaluation. Range (min … max): 68.149 ms … 104.358 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 77.456 ms ┊ GC (median): 0.00% Time (mean ± σ): 80.173 ms ± 9.858 ms ┊ GC (mean ± σ): 6.67% ± 8.31 % ▆█ █▄ ▂▄ █▆██▁▁▄▁▁▁▁▁▁▁▁▁▁▆▆▁██▆▁▄▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▄▁▄ ▁ 68.1 ms Histogram: frequency by time 94.8 ms < Memory estimate: 42.78 MiB, allocs estimate: 1253404. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 145 samples with 1 evaluation. Range (min … max): 29.232 ms … 139.283 ms ┊ GC (min … max): 0.00% … 0.00 % Time (median): 30.997 ms ┊ GC (median): 0.00% Time (mean ± σ): 32.506 ms ± 9.228 ms ┊ GC (mean ± σ): 0.23% ± 1.93 % ▁▆█▇▆▃▁ ▃▆███████▅▄▃▃▃▃▃▃▁▅▅▄▃▁▁▃▁▃▃▃▁▁▁▃▃▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▃ 29.2 ms Histogram: frequency by time 46.4 ms < Memory estimate: 781.86 KiB, allocs estimate: 7. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` ```julia @model function demo4_dotted(n, ::Type{TV}=Vector{Float64}) where {TV} m ~ Normal() x = TV(undef, n) x .~ Normal(m, 1.0) end model_def = demo4_dotted data = (100_000, ); ``` ```julia @time model_def(data)(); ``` ``` 1.421197 seconds (5.08 M allocations: 375.131 MiB, 6.23% gc time, 0.62% c ompilation time) ``` ```julia m = time_model_def(model_def, data); ``` ``` 0.000002 seconds (2 allocations: 64 bytes) ``` ```julia suite = make_suite(m); results = run(suite); ``` ```julia results["evaluation_untyped"] ``` ``` BenchmarkTools.Trial: 39 samples with 1 evaluation. Range (min … max): 108.605 ms … 348.289 ms ┊ GC (min … max): 9.70% … 9. 23% Time (median): 118.470 ms ┊ GC (median): 15.38% Time (mean ± σ): 121.407 ms ± 37.585 ms ┊ GC (mean ± σ): 13.35% ± 3. 15% ▆ █ █▁█▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 109 ms Histogram: frequency by time 348 ms < Memory estimate: 347.69 MiB, allocs estimate: 963583. ``` ```julia results["evaluation_typed"] ``` ``` BenchmarkTools.Trial: 61 samples with 1 evaluation. Range (min … max): 66.380 ms … 350.632 ms ┊ GC (min … max): 9.01% … 4.7 7% Time (median): 73.635 ms ┊ GC (median): 16.29% Time (mean ± σ): 75.751 ms ± 35.996 ms ┊ GC (mean ± σ): 12.78% ± 3.8 9% █ ▄ ▃ ▇█▆▆▄▄▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▆████▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃ ▁ 66.4 ms Histogram: frequency by time 84.5 ms < Memory estimate: 337.55 MiB, allocs estimate: 399306. ``` ```julia if WEAVE_ARGS[:include_typed_code] typed = typed_code(m) end ``` </details>
- Loading branch information