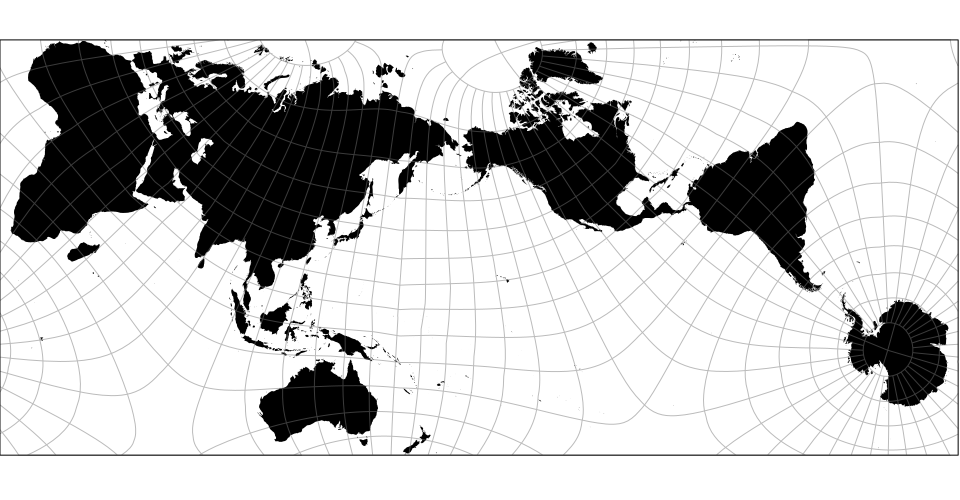
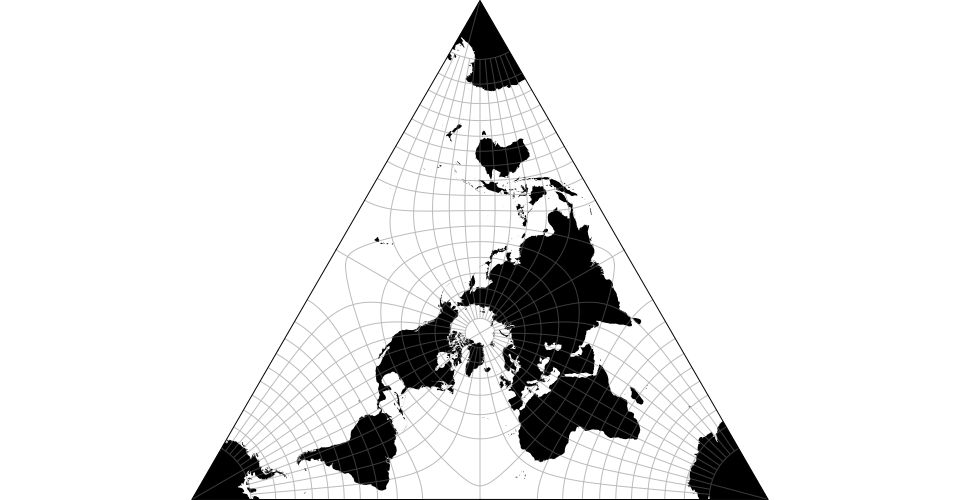
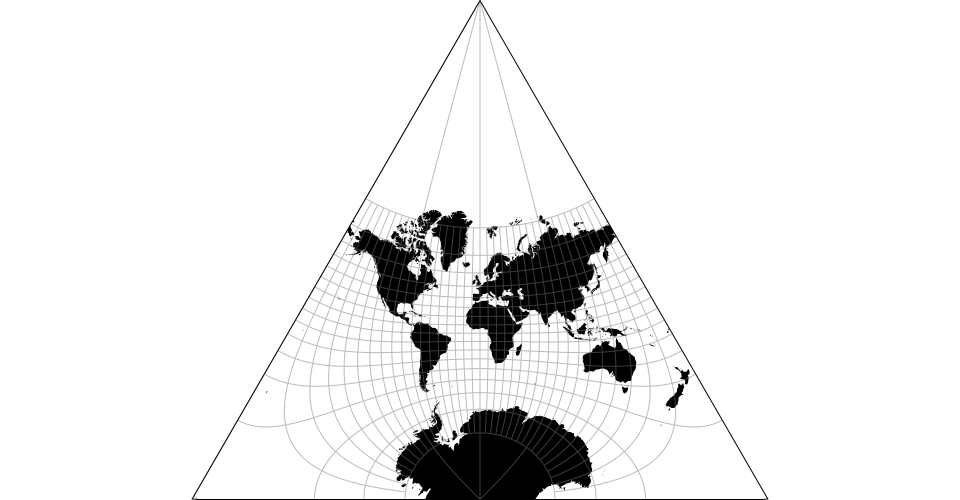
Clipping and geometric operations for spherical polygons.
If you use NPM, npm install d3-geo-polygon. Otherwise, download the latest release. You can also load directly from unpkg. AMD, CommonJS, and vanilla environments are supported. In vanilla, a d3 global is exported:
<script src="https://unpkg.com/d3-geo@1"></script>
<script src="https://unpkg.com/d3-geo-polygon@1"></script>
<script>
// new projection
var projection = d3.geoDodecahedral();
// polyhedral projections don’t need SVG or canvas clipping anymore
var projection = d3.geoPolyhedralCollignon();
// arbitrary polygon clipping on any projection
var projection = d3.geoEquirectangular()
.preclip(d3.geoClipPolygon({
type: "Polygon",
coordinates: [[[-10, -10], [-10, 10], [10, 10], [10, -10], [-10, -10]]]
}));
</script># d3.geoClipPolygon(polygon) · Source, Examples
Given a GeoJSON polygon or multipolygon, returns a clip function suitable for projection.preclip.
# clip.polygon()
Given a clipPolygon function, returns the GeoJSON polygon.
# d3.geoIntersectArc(arcs) · Source, Examples
Given two spherical arcs [point0, point1] and [point2, point3], returns their intersection, or undefined if there is none. See “Spherical Intersection”.
d3-geo-polygon adds polygon clipping to the polyhedral projections from d3-geo-projection. Thus, it supercedes the following symbols:
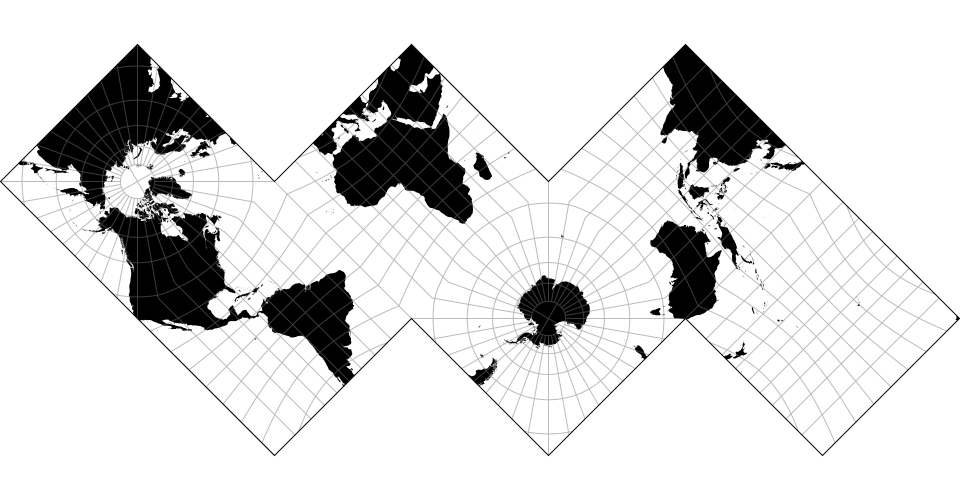
# d3.geoPolyhedral(tree, face) · Source, Examples
Defines a new polyhedral projection. The tree is a spanning tree of polygon face nodes; each node is assigned a node.transform matrix. The face function returns the appropriate node for a given lambda and phi in radians.
# polyhedral.tree() returns the spanning tree of the polyhedron, from which one can infer the faces’ centers, polygons, shared edges etc.
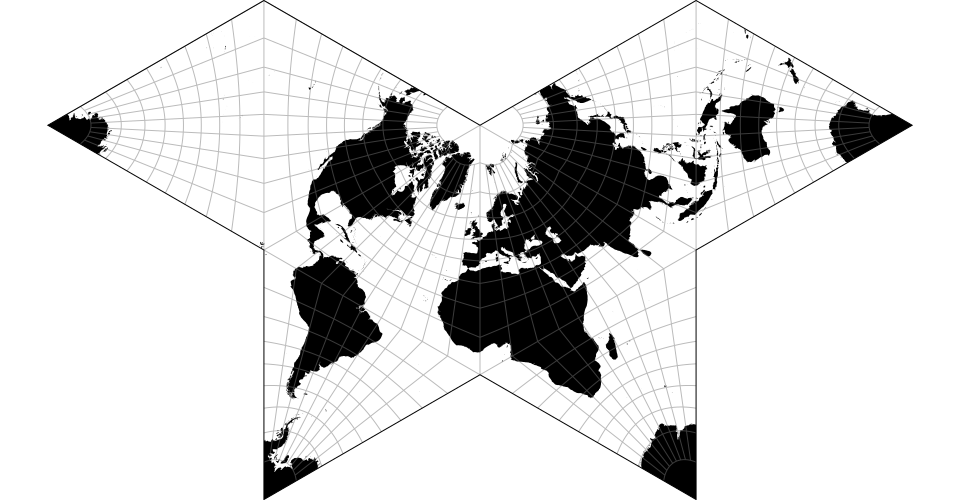
# d3.geoPolyhedralButterfly() · Source
The gnomonic butterfly projection.
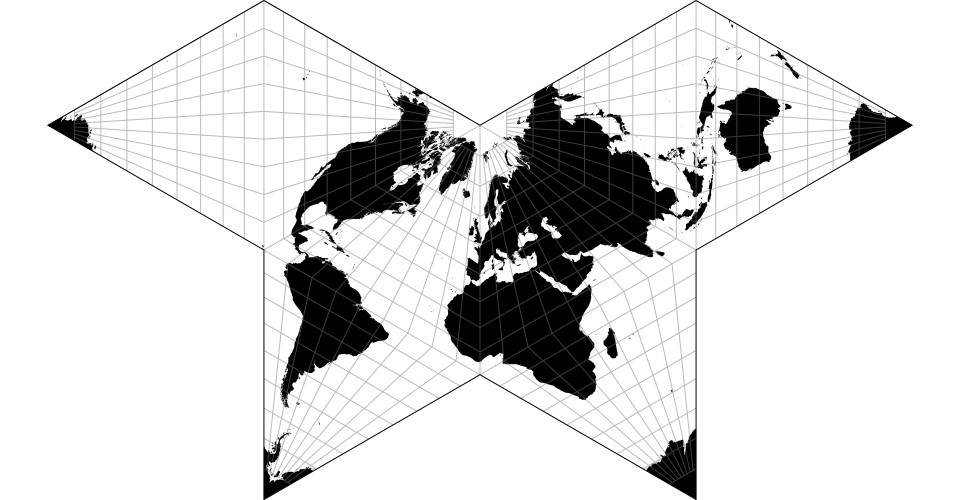
# d3.geoPolyhedralCollignon() · Source
The Collignon butterfly projection.
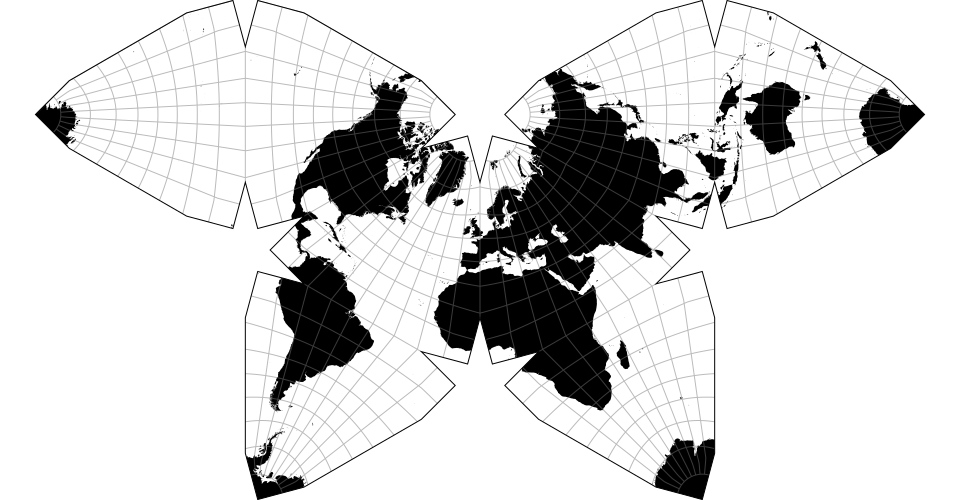
# d3.geoPolyhedralWaterman() · Source
A butterfly projection inspired by Steve Waterman’s design.
New projections are introduced:
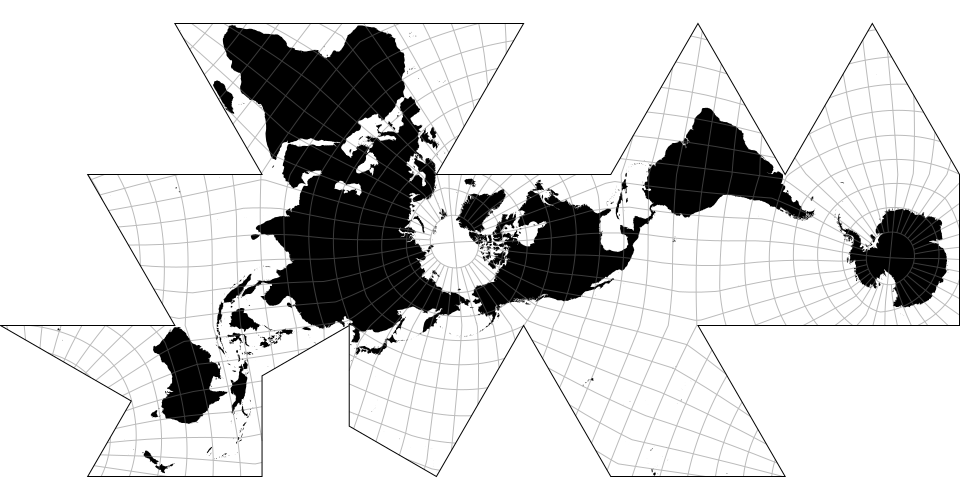
# d3.geoPolyhedralVoronoi([parents], [polygons], [faceProjection], [faceFind]) · Source
Returns a polyhedral projection based on the polygons, arranged in a tree according to the parents list. polygons are a GeoJSON FeatureCollection of geoVoronoi cells, which should indicate the corresponding sites (see d3-geo-voronoi). An optional faceProjection is passed to d3.geoPolyhedral() -- note that the gnomonic projection on the polygons’ sites is the only faceProjection that works in the general case.
The .parents([parents]), .polygons([polygons]), .faceProjection([faceProjection]) set and read the corresponding options. Use .faceFind(voronoi.find) for faster results.
# d3.geoCubic() · Source, Examples
The cubic projection.
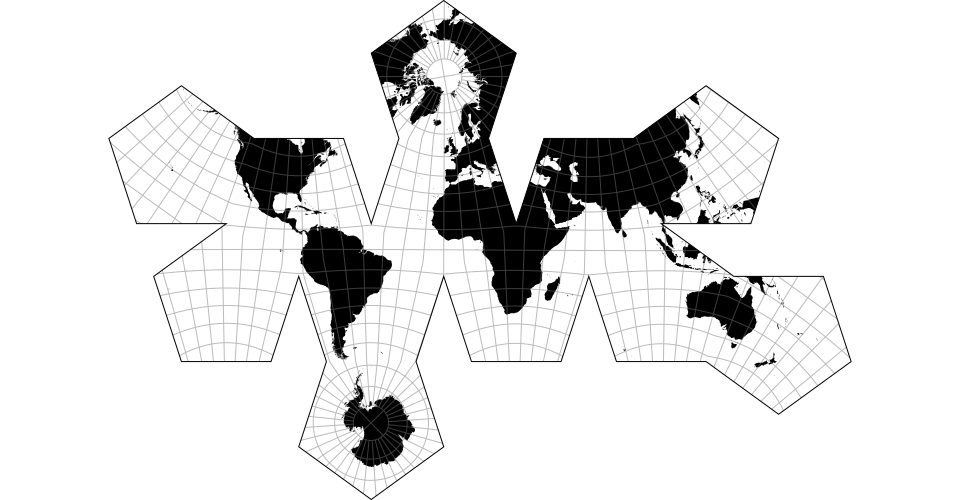
# d3.geoDodecahedral() · Source, Examples
The dodecahedral projection.
# d3.geoIcosahedral() · Source, Examples
The icosahedral projection.
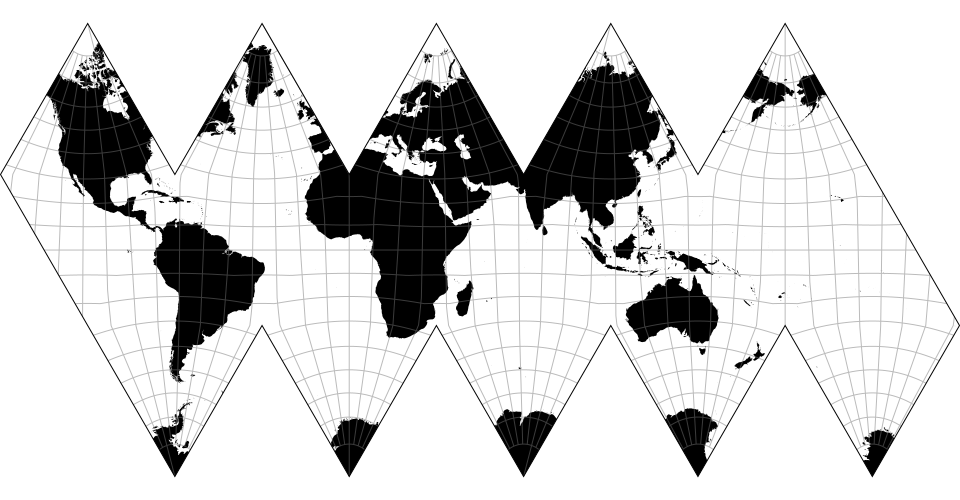
# d3.geoAirocean() · Source, Examples
Buckminster Fuller’s Airocean projection (also known as “Dymaxion”), based on a very specific arrangement of the icosahedron which allows continuous continent shapes. Fuller’s triangle transformation, as formulated by Robert W. Gray (and implemented by Philippe Rivière), makes the projection almost equal-area.
# d3.geoCahillKeyes() · Source, Examples
# d3.geoCahillKeyes
The Cahill-Keyes projection, designed by Gene Keyes (1975), is built on Bernard J. S. Cahill’s 1909 octant design. Implementation by Mary Jo Graça (2011), ported to D3 by Enrico Spinielli (2013).
# d3.geoImago() · Source, Examples
The Imago projection, engineered by Justin Kunimune (2017), is inspired by Hajime Narukawa’s AuthaGraph design (1999).
# imago.k([k])
Exponent. Useful values include 0.59 (default, minimizes angular distortion of the continents), 0.68 (gives the closest approximation of the Authagraph) and 0.72 (prevents kinks in the graticule).
# imago.shift([shift])
Horizontal shift. Defaults to 1.16.
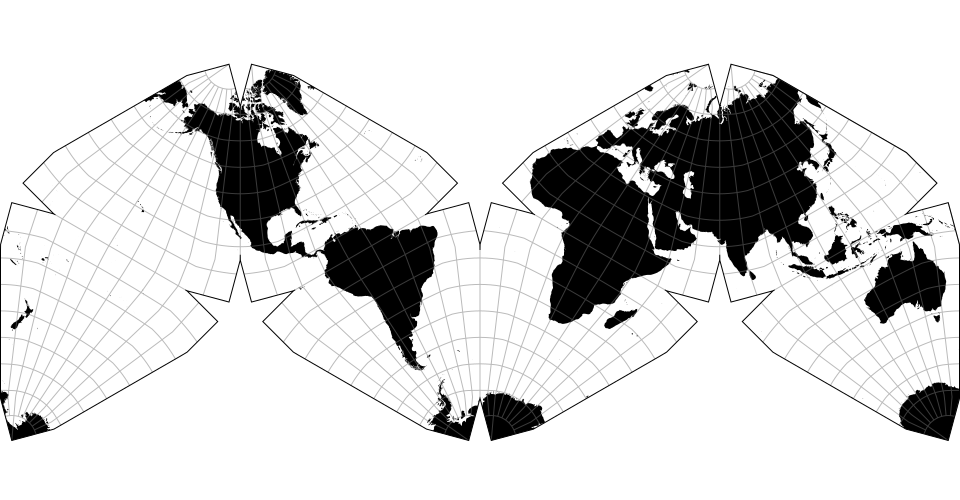
# d3.geoTetrahedralLee() · Source, Examples
# d3.geoLeeRaw
Lee’s tetrahedral conformal projection.
# Default angle is +30°, apex up (-30° for base up, apex down).
Default aspect uses projection.rotate([30, 180]) and has the North Pole at the triangle’s center -- use projection.rotate([-30, 0]) for the South aspect.
# d3.geoCox() · Source, Examples
# d3.geoCoxRaw
The Cox conformal projection.
# d3.geoComplexLog([planarProjectionRaw[, cutoffLatitude]]) · Source, Example
# d3.geoComplexLogRaw([planarProjectionRaw])
Complex logarithmic view. This projection is based on the papers by Joachim Böttger et al.:
- Detail‐In‐Context Visualization for Satellite Imagery (2008)
- Complex Logarithmic Views for Small Details in Large Contexts (2006)
The specified raw projection planarProjectionRaw is used to project onto the complex plane on which the complex logarithm is applied. Recommended are azimuthal equal-area (default) or azimuthal equidistant.
cutoffLatitude is the latitude relative to the projection center at which to cutoff/clip the projection, lower values result in more detail around the projection center. Value must be < 0 because complex log projects the origin to infinity.
# complexLog.planarProjectionRaw([projectionRaw])
If projectionRaw is specified, sets the planar raw projection. See above. If projectionRaw is not specified, returns the current planar raw projection.
# complexLog.cutoffLatitude([latitude])
If latitude is specified, sets the cutoff latitude. See above. If latitude is not specified, returns the current cutoff latitude.