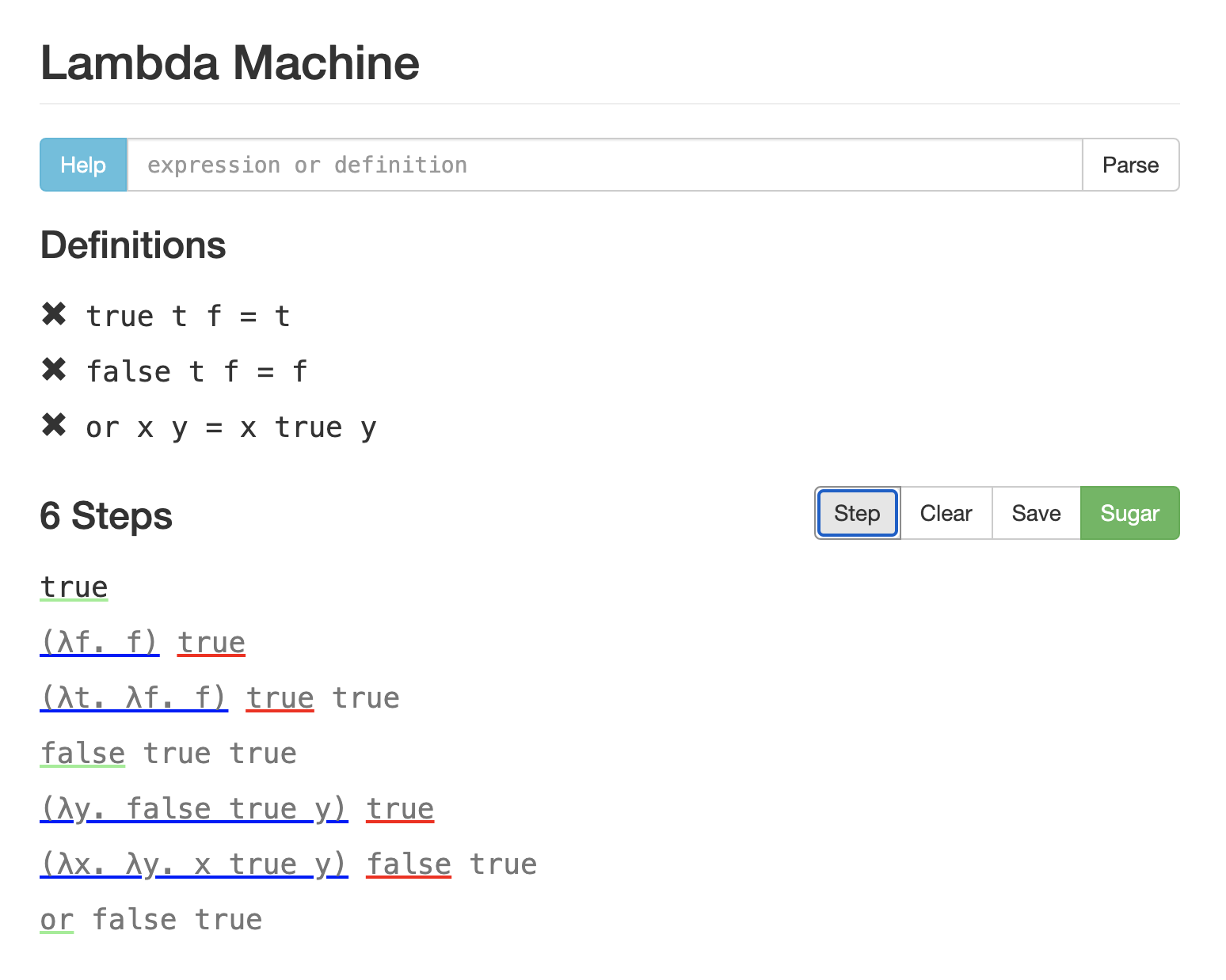
Try it here! It's a machine for evaluating expressions in the untyped lambda calculus. This machine has everything:
- Lambdas
- Variables
- Applications
- Recursive top-level definitions (I finally caved)
- Uh, that's it
Yep. Here's a grammar, if you like that kind of thing. I know I do.
definition
= name, {name}, "=", expression ; (* Definition *)
expression
= lambda, name, {name}, ".", expression (* Lambda abstraction *)
| name (* Variable *)
| expression, expression (* Application *)
| "(", expression, ")" (* Parentheses *)
| {digit} (* Natural number *)
| "[", [expressions], "]" (* List *)
;
expressions
= expression, [",", expressions] ; (* One or more comma-separated expressions *)
lambda
= "\" (* Backslash *)
| "λ" (* Greek letter lambda *)
;
name
= (letter | "_") (* Initial letter or underscore *)
, {letter | "-"} (* Zero or more letters or hyphens *)
, ["?"] (* Optional question mark *)
, {subscript | digit} (* Zero or more subscripts or digits *)
;
letter (* Lowercase latin letters *)
= "a" | "b" | "c" | "d" | "e" | "f" | "g"
| "h" | "i" | "j" | "k" | "l" | "m" | "n"
| "o" | "p" | "q" | "r" | "s" | "t" | "u"
| "v" | "w" | "x" | "y" | "z" ;
subscript (* Subscripts *)
= "₀" | "₁" | "₂" | "₃" | "₄" | "₅" | "₆"
| "₇" | "₈" | "₉" ;
digit (* Decimal digits *)
= "0" | "1" | "2" | "3" | "4" | "5" | "6"
| "7" | "8" | "9" ;Natural numbers and lists are desugared to plain lambda calculus during parsing. A natural number n is parsed as a function that applies s to z n times.
0 -> \s. \z. z
1 -> \s. \z. s z
2 -> \s. \z. s (s z)
3 -> \s. \z. s (s (s z))
4 -> \s. \z. s (s (s (s z)))
A list is parsed as a right fold over its elements using cons and nil.
[a] -> \cons. \nil. cons a nil
[a, b] -> \cons. \nil. cons a (cons b nil)
[a, b, c] -> \cons. \nil. cons a (cons b (cons c nil))
These work together too:
[0, 1, 2] -> \cons. \nil. cons (\s. \z. z) (cons (\s. \z. s z) (cons (\s. \z. s (s z)) nil))
I've been working through the exercises in
Introduction to Functional Programming Through Lambda Calculus
by Greg Michaelson, and some of these expressions are tedious
to reduce by hand. I build this to do it for me.
Lol, I'm not doing that anymore. At this point, it's mostly just a fun way for me to fiddle around with PureScript. Hopefully, it's also useful to someone learning the lambda calculus for the first time. Let me know if you're using it and how I can make it better.
Lambda Machine is written in PureScript and React using the purescript-react-basic bindings. Expressions are converted to a locally nameless representation before being evaluated in normal order using call-by-need. Specifically, I use a tweaked version of the Template Instantiation Machine described in Simon Peyton Jones' and David Lester's Implementing Functional Languages: A Tutorial.
The Template Instantiation Machine is a graph reduction interpreter that is typically considered too slow and inflexible for "real" language implementations. However, for Lambda Machine, I only care about retaining or reconstructing enough syntactic information to easily visualize incremental lazy evaluation for humans. Speed is not the goal, so the Template Instantiation Machine works just fine.
Tweaks:
- The Template Instantiation Machine operates on lambda-lifted supercombinators. Lambda Machine creates closures at runtime.
- The Template Instantiation Machine applies functions to as many arguments as are available on the stack. Lambda Machine applies functions one argument at a time, like a person working with pen and paper might.
- The Template Instantiation Machine does not evaluate under lambdas. Lambda Machine does. This makes certain functions (e.g. the predecessor function on Church numerals) work that would otherwise get stuck too early.
- The Template Instantiation calls its stack-of-suspended-stacks the "dump". Lambda Machine calls its stack-of-suspended-stacks the "stash". I don't remember why I did this. Maybe I thought "stash" looked nicer next to "stack". Maybe I thought "dump" was too ugly of a word to be typing so much. Truly, it is a mystery lost to time.
Anyway, build and run it like this:
cd frontend
yarn setup
yarn build
yarn start(Or, again, just go here.)
Me, Chris Parks, hi, hello, how are you? Let me know if you have questions, comments, or, like, really good sandwich recipes.