Pattern and Sequence Predictor (PSP) is an unsupervised Machine Intelligence architecture based on intelligence principles of the neocortex, the predictive nature of animal brains, and the theories of Numenta's Hierarchical Temporal Memory. The architecture is coded in C++ using the OpenCL parallel processing framework. Working operating systems include Linux and Windows. The only dependancy needed to run PSP is an OpenCL installation.
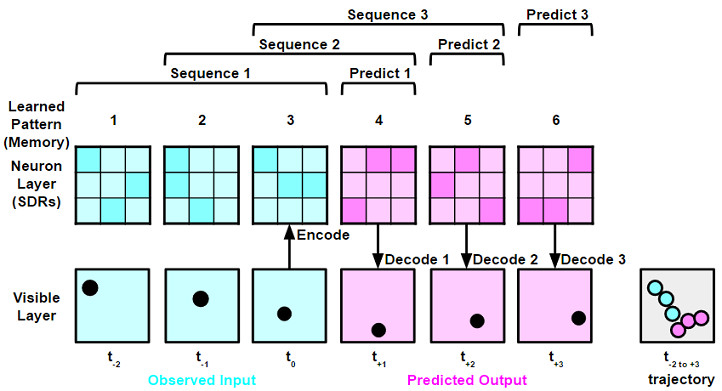
When given a stimulus, like patterns of light seen by the eye, a sparse set of neurons in the neocortex are "active", meaning only a few neurons of a relatively large population output spikes of action potentials. Any stimuli, be it light, sound, touch, etc., may be converted into neuron activations. Therefore, the "language" of the neocortex is patterns and sequences of sparse neuron activations. By observing sequences of patterns over time, the neocortex is able to learn and recognize reoccouring sequence trajectories and predict immediate future patterns and sequences. The figure below gives a visual example of this in action.
At a single time step (t = 0), the visual input of a ball gets converted into neuron activations (an array of 0s and 1s). In this case the algorithm recognizes that this particular set of neuron activations is "pattern 3". Previous time steps (t = -1, t = -2) have already converted and recognized previously learned neuron patterns from memory. Not only does the algorithm learn patterns throughout its operational history, it also learns sequences. By recognizing a learned sequence PSP can predict the next time step's pattern. For example, the occourance of "pattern 1" then "pattern 2" then "pattern 3" often leads to "pattern 4" occouring in the future. By adding the predicted pattern to a rotating sequence, PSP can keep predicting future patterns as far as necessary.
The above figure demonstrates PSP's 4 core functions:
- Spatial Encoding: Encodes spatial-temporal sensory-motor input into a sparsly distributed neuron activation pattern
- Temporal Encoding (Prediction): Predicts the most likely future pattern
- Spatial Decoding: Decodes future pattern into visible spatial-temporal sensory-motor outputs
- Learning: Learns new neuron activation patterns and sequences of patterns
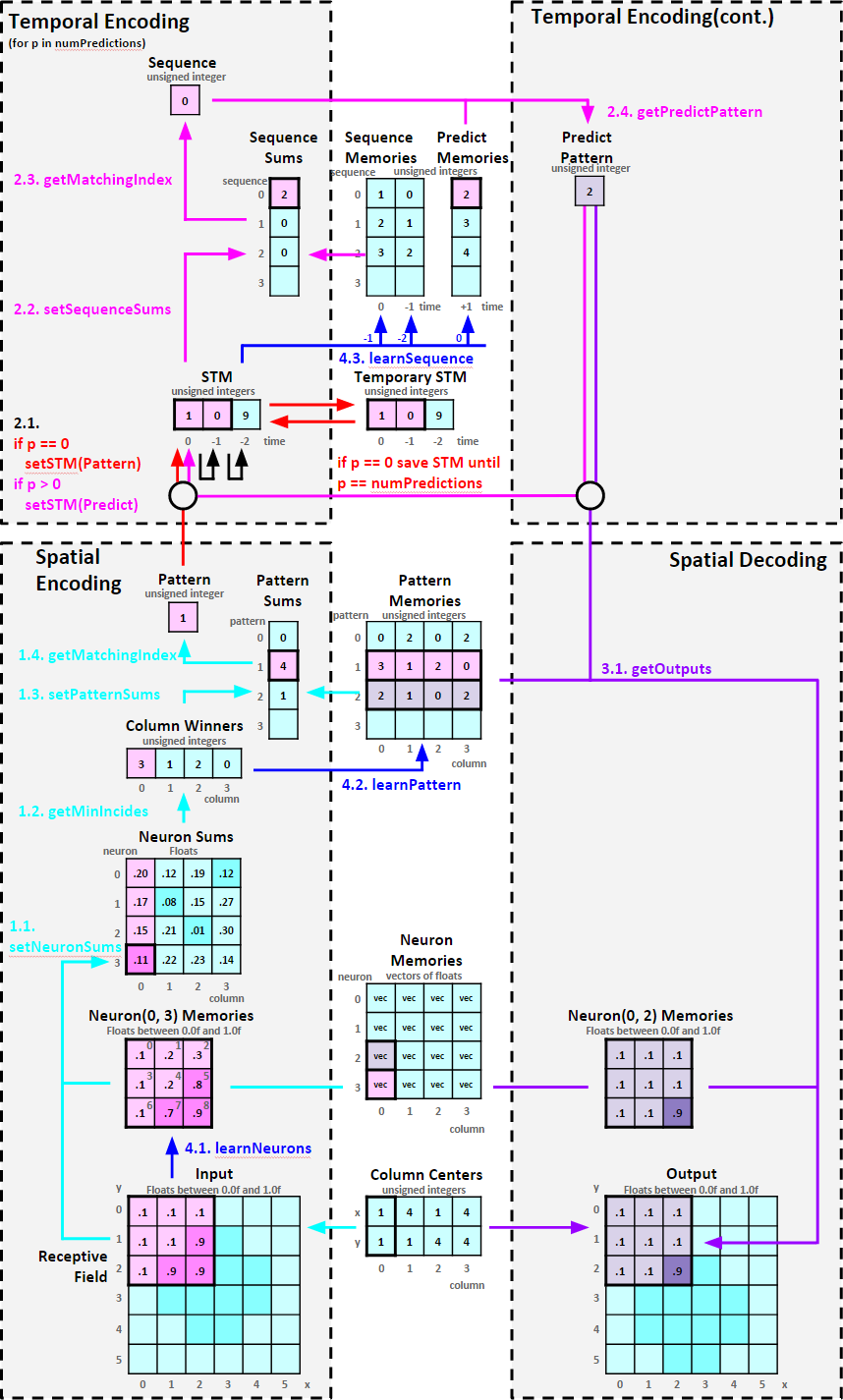
The figure below shows a code flow diagram of the PSP algorithm. The flow of operations start on the bottom left and travels in a clockwise direction. Each function is explained in order.
At every time step Spatial Encoding represents an observed input space as a Sparse Distributed Eepresentation (SDR) of neuron activations. The algorithm then tries to match the SDR to a bank of SDRs called "Pattern Memories". If a match is found, the index of the matching SDR in the bank is the "Pattern Memory". If no match is found, learning occours.
Programatically each column behaves like a Self Organizing Map, an unsupervised learning technique used for dimensionality reduction(reducing the near infinite possibilites of an input space into a limited set of descrete activations). The column is centered at a specified location on the input space and observes a receptive field, a specified size of the input space.
Each column tries calculate the best matching neuron by calculating the Euclidian distance formula between the neuron's memories and the column's observed receptive field values. The Euclidian distance indicates the level of similarity between two sets of values. A short distance means the values are similar while a long distance means the values are different.
The Euclidian Distance Formula:
for every memory m: sum += (input[m] - memory[m])^2
Therefore, the output of this fuction is a 2D array of floats called "Neuron Sums" representing how well each column's neuron memories match with the input data of the column's respective receptive field.
For each column, the neuron with the smallest distance is the best matching neuron and it's integer index gets written to "Column Winners". Thus the output of this function is a vector of integers representing a SDR of column neuron activations.
The algorithm stores SDRs in a bank called "Pattern Memories" where each row contains previously learned "Column Winners". At each time step the algorithm compares "Column Winners" with each row in "Pattern Memories". Each equivalent value increments the row's sum by 1.
This function looks at each row of "Pattern Sums" and if the sum is equal to the number of columns, the row index is stored in "Pattern". This stored value represents the row index of "Pattern Memories" that matches "Column Winners". If no rows match, the next available empty row index value is used.
At every time step Temporal Encoding updates a running memory of observed patterns from Spatial Encoding and attempts to recognize a learned sequence. If it recognizes a sequence, the algorithm outputs a prediction of the next time step's pattern. By feeding this predicted pattern back through more iterations of Temporal Encoding, the algorithm outputs the pattern prediction many time steps ahead of the current time step.
"Short Term Memory" ("STM") holds a running sequence of patterns from Spatial Encoding. Each index of "STM" represents a historical time step, i.e. index 0 is t = 0, index 1 is t = -1, index 2 is t = -2 and so on. Before "STM" is updated with the current or predicted pattern, the algorithm shifts previous patterns back through time. For example, the pattern in index 0 moves to index 1, the pattern in index 1 moves to index 2, and so on. Then the current or predicted pattern is copied into index 0.
At a given time step for the first iteration of Temporal Encoding, "STM" shifts and the observed pattern from Spatial Encoding is placed into index 0 then the current values of "STM" are copied into a buffer called "Temporary STM". During the same time step for subsequent iterations of Temporal Encoding, "STM" shifts and predicted patterns are placed into index 0. After the last iteration of Temporal Encoding is finished for the given time step, the values of the "Temporary STM" are copied back into "STM". This allows PSP maintain the actually observed sequences in its short term memory.
The algorithm stores "STM" index 0 in a bank called "Predict Memories" and every index above index 0 in a bank called "Sequence Memories". At each time step the algorithm compares "STM" with each row in "Sequence Memories", exactly like the function in Spatial Encoding. Each equivalent value increments the row's sum by 1.
This function looks at each row of "Sequence Sums" and if the sum is equal to the number of patterns in "STM" minus 1, the row index is stored in "Sequence". Much like the function in Spatial Encoding, this stored value represents the row index of "Sequence Memories" that matches "STM". If no rows match, the next available empty row index value is used.
This function sets the "Predict Pattern" value by retrieving the value in "Predict Memories" at the index given by the "Sequence" value.
Spatial Decoding converts "Predict Pattern" into visible outputs. It does this by retrieving a SDR in "Pattern Memories" at the index of the value of "Predict Pattern". The function then uses each column's neuron memories to reconstruct a visual output. Decoding can be thought of as PSP "communicating" possible future patterns.
Once Temporal Memory has completed its predicting and have a value in Predict Pattern, the algorithm grabs the appropriate column winner SDR from Pattern Memories. Using this set of column winners, the algorithm looks up each winner neuron's memories and applies the memories to the output receptive field of each column.
If Column Winners values are not in Pattern Memories, add those values to Pattern Memories.
If Short Term Memory values at index 1 and above are not in Sequence Memories, add those values to Sequence Memories. Additionally, the Short Term Memory value at index 0 is added Predict Memories at the same row location of the new sequence in Sequence Memories.