This repo provides an evolving set of instructional guides for using the GerryChain package for generating dual graph partitions. More detailed technical documentation can be found here and my introduction to the mathematics of Markov chains and MCMC for redistrcitng can be found here: (pdf) (webpage) (GitHub).
These templates assume that you have already installed GerryChain (see here or here for directions) and are ready to start building your own ensembles. Since some of the examples use real-world data, you should clone this repo to your computer - this will also make it easy to get access to updates to the templates. Once you have downloaded everything you should be able to run the templates individually by navigating to the appropriate subfolder and entering:python grid_chain_simple.pyHere are links to the current templates:
- Grids
- Pennsylvania
- Alaska
The best place to start is with the simple grids example. This template breaks the code into pieces, building the graph and partition components separately before doing a couple of small runs to compare ReCom to Flip. We start by importing the packages we need:
import os
import random
import json
import geopandas as gpd
import functools
import datetime
import matplotlib
#matplotlib.use('Agg')
import matplotlib.pyplot as plt
import numpy as np
import csv
from networkx.readwrite import json_graph
import math
from functools import partial
import networkx as nx
import numpy as np
from gerrychain import Graph
from gerrychain import MarkovChain
from gerrychain.constraints import (Validator, single_flip_contiguous,
within_percent_of_ideal_population, UpperBound)
from gerrychain.proposals import propose_random_flip, propose_chunk_flip
from gerrychain.accept import always_accept
from gerrychain.updaters import Election,Tally,cut_edges
from gerrychain import GeographicPartition
from gerrychain.partition import Partition
from gerrychain.proposals import recom
from gerrychain.metrics import mean_median, efficiency_gapNext we build a gn x k by gn x k graph split into k vertical columns:
#BUILD GRAPH
gn=6
k=5
ns=50
p=.5
graph=nx.grid_graph([k*gn,k*gn])
for n in graph.nodes():
graph.node[n]["population"]=1
if random.random()<p:
graph.node[n]["pink"]=1
graph.node[n]["purple"]=0
else:
graph.node[n]["pink"]=0
graph.node[n]["purple"]=1
if 0 in n or k*gn-1 in n:
graph.node[n]["boundary_node"]=True
graph.node[n]["boundary_perim"]=1
else:
graph.node[n]["boundary_node"]=False
#this part adds queen adjacency
#for i in range(k*gn-1):
# for j in range(k*gn):
# if j<(k*gn-1):
# graph.add_edge((i,j),(i+1,j+1))
# graph[(i,j)][(i+1,j+1)]["shared_perim"]=0
# if j >0:
# graph.add_edge((i,j),(i+1,j-1))
# graph[(i,j)][(i+1,j-1)]["shared_perim"]=0
########## BUILD ASSIGNMENT
cddict = {x: int(x[0]/gn) for x in graph.nodes()}
######PLOT GRIDS
plt.figure()
nx.draw(graph, pos = {x:x for x in graph.nodes()} ,node_size = ns, node_shape ='s')
plt.show()
cdict = {1:'pink',0:'purple'}
plt.figure()
nx.draw(graph, pos = {x:x for x in graph.nodes()}, node_color = [cdict[graph.node[x]["pink"]] for x in graph.nodes()],node_size = ns, node_shape ='s' )
plt.show()
plt.figure()
nx.draw(graph, pos = {x:x for x in graph.nodes()}, node_color = [cddict[x] for x in graph.nodes()] ,node_size = ns, node_shape ='s',cmap = 'tab20')
plt.show()| Original Graph | Random Vote Data | Initial Partition |
 |  |  |
Next we configure the partitions, updaters, and constraints.
####CONFIGURE UPDATERS
def step_num(partition):
parent = partition.parent
if not parent:
return 0
return parent["step_num"] + 1
updaters = {'population': Tally('population'),
'cut_edges': cut_edges,
'step_num': step_num,
"Pink-Purple": Election("Pink-Purple", {"Pink":"pink","Purple":"purple"})}
#########BUILD PARTITION
grid_partition = Partition(graph,assignment=cddict,updaters=updaters)
#ADD CONSTRAINTS
popbound=within_percent_of_ideal_population(grid_partition,.1)
#########Setup Proposal
ideal_population = sum(grid_partition["population"].values()) / len(grid_partition)
tree_proposal = partial(recom,
pop_col="population",
pop_target=ideal_population,
epsilon=0.05,
node_repeats=1
)
#######BUILD MARKOV CHAINS
recom_chain=MarkovChain(tree_proposal, Validator([popbound]),accept=always_accept,
initial_state=grid_partition, total_steps=100)
boundary_chain=MarkovChain(propose_random_flip, Validator([single_flip_contiguous, popbound]),accept=always_accept,
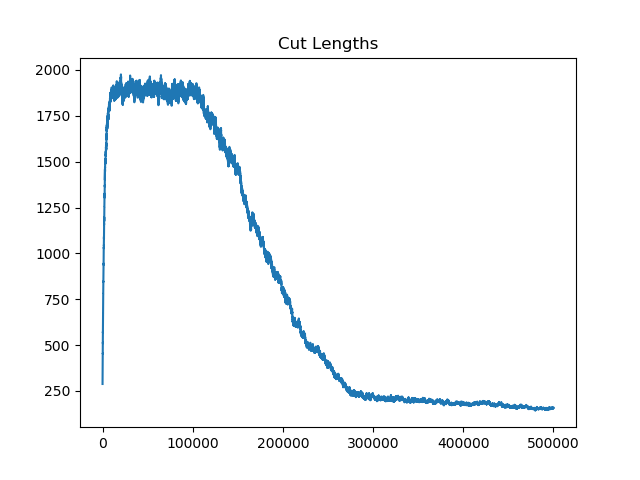
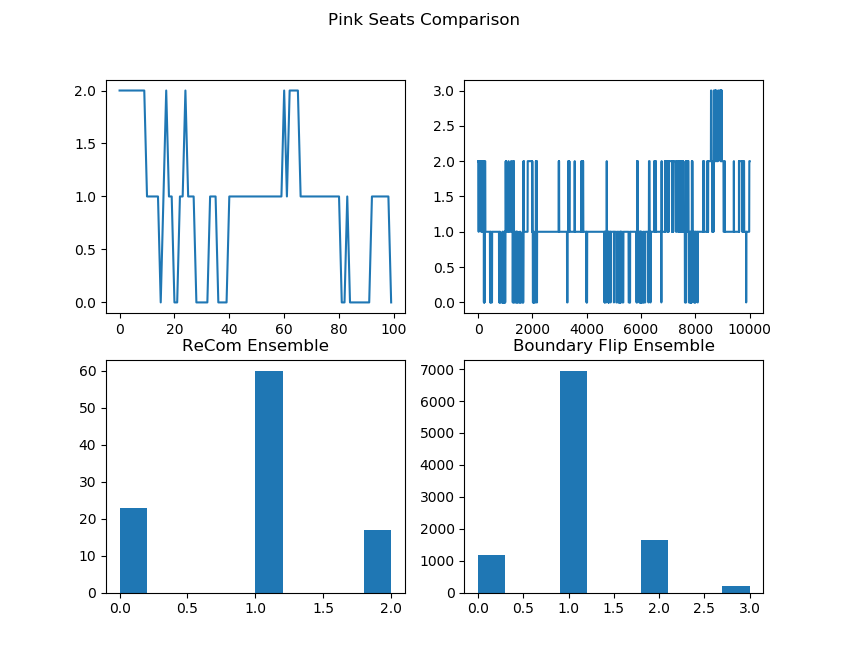
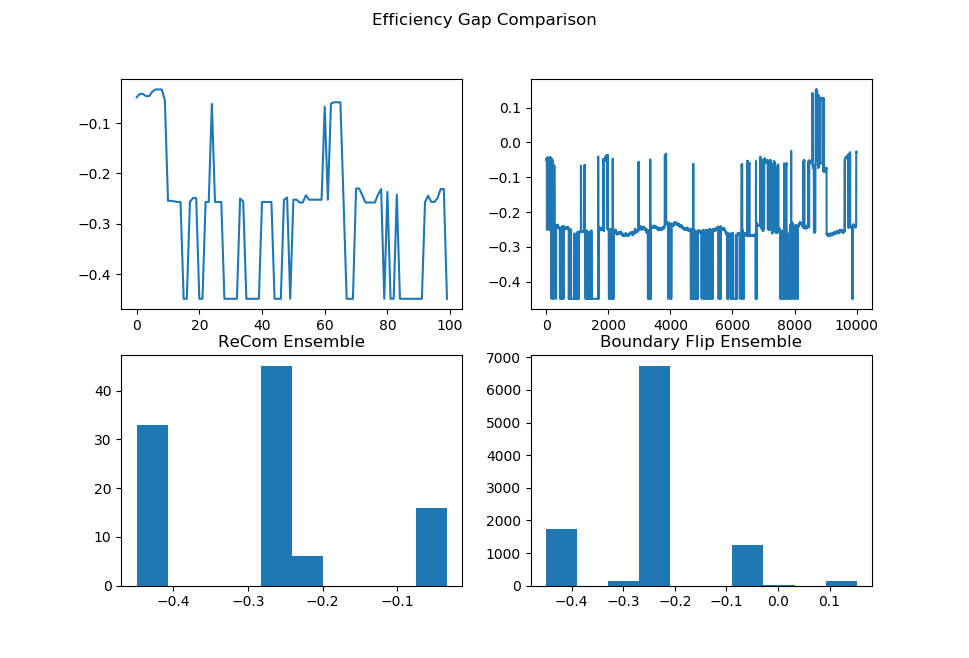
initial_state=grid_partition, total_steps=10000)Finally, we run two chains, one with each proposal method, and record a variety of statistics. The final state of each of the two chains will be displayed. Notice that even though the ReCom chain only takes 100 steps, it travels much further than the 10,000 step boundary chain.
#########Run MARKOV CHAINS
rsw = []
rmm = []
reg = []
rce = []
for part in recom_chain:
rsw.append(part["Pink-Purple"].wins("Pink"))
rmm.append(mean_median(part["Pink-Purple"]))
reg.append(efficiency_gap(part["Pink-Purple"]))
rce.append(len(part["cut_edges"]))
"""
plt.figure()
nx.draw(graph, pos = {x:x for x in graph.nodes()}, node_color = [dict(part.assignment)[x] for x in graph.nodes()] ,node_size = ns, node_shape ='s',cmap = 'tab20')
plt.savefig(f"./Figures/recom_{part['step_num']:02d}.png")
plt.close()
"""
plt.figure()
nx.draw(graph, pos = {x:x for x in graph.nodes()}, node_color = [dict(part.assignment)[x] for x in graph.nodes()] ,node_size = ns, node_shape ='s',cmap = 'tab20')
plt.show()
bsw = []
bmm = []
beg = []
bce = []
for part in boundary_chain:
bsw.append(part["Pink-Purple"].wins("Pink"))
bmm.append(mean_median(part["Pink-Purple"]))
beg.append(efficiency_gap(part["Pink-Purple"]))
bce.append(len(part["cut_edges"]))
"""
plt.figure()
nx.draw(graph, pos = {x:x for x in graph.nodes()}, node_color = [dict(part.assignment)[x] for x in graph.nodes()] ,node_size = ns, node_shape ='s',cmap = 'tab20')
plt.savefig(f"./Figures/boundary_{part['step_num']:04d}.png")
plt.close()
"""
plt.figure()
nx.draw(graph, pos = {x:x for x in graph.nodes()}, node_color = [dict(part.assignment)[x] for x in graph.nodes()] ,node_size = ns, node_shape ='s',cmap = 'tab20')
plt.show()| ReCom Ensemble | Boundary Ensemble |
 |  |
After the chain runs, we make some plots comparing the behavior of the ensembles.
##################Partisan Plots
names = ["Cut Edges", "Mean Median", "Pink Seats", "Efficiency Gap"]
lists = [[rce, bce], [rmm, bmm], [rsw, bsw], [reg, beg]]
for z in range(4):
plt.figure()
plt.suptitle(f"{names[z]} Comparison")
plt.subplot(2, 2, 1)
plt.plot(lists[z][0])
plt.subplot(2, 2, 3)
plt.hist(lists[z][0])
plt.title("ReCom Ensemble")
plt.subplot(2, 2, 2)
plt.plot(lists[z][1])
plt.subplot(2, 2, 4)
plt.hist(lists[z][1])
plt.title("Boundary Flip Ensemble")
fig = plt.gcf()
fig.set_size_inches((8,7))
plt.show() |  |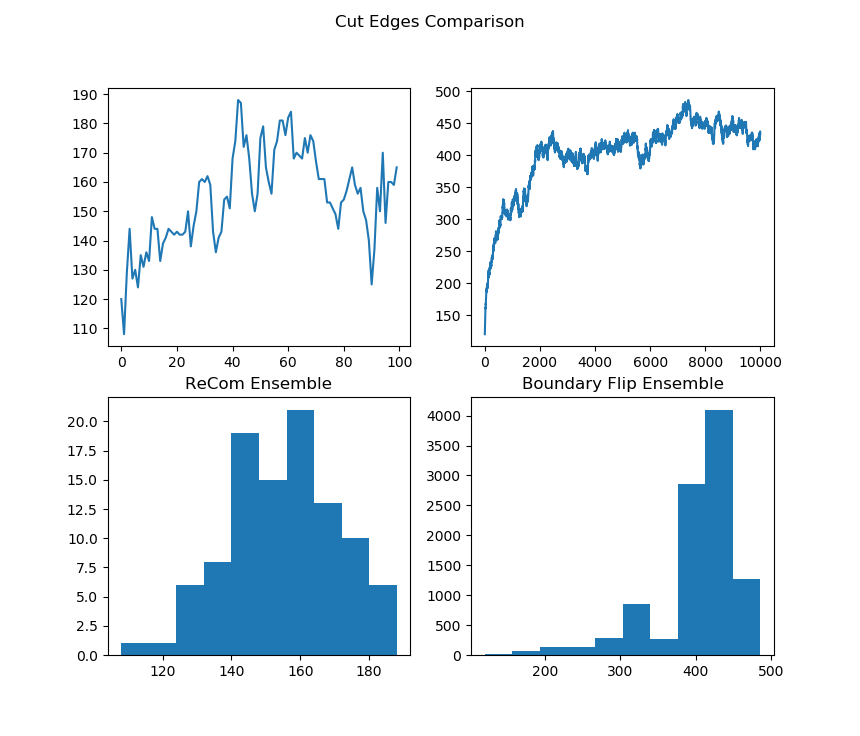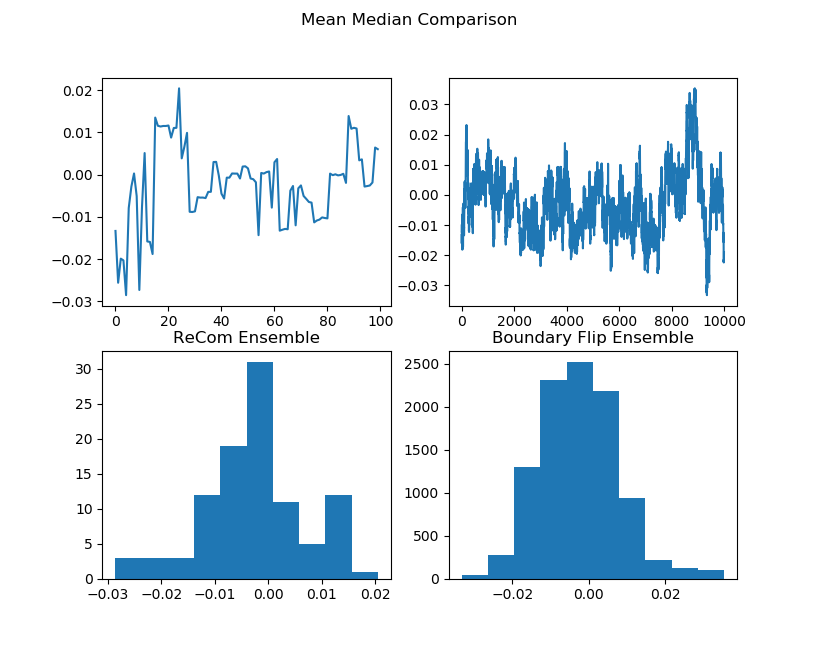
 |
 |
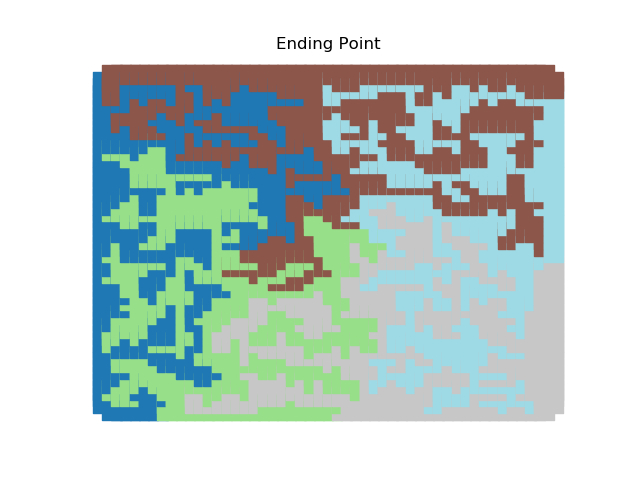
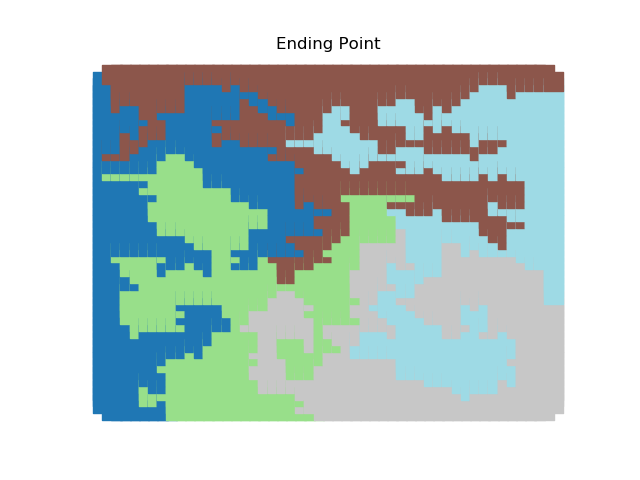
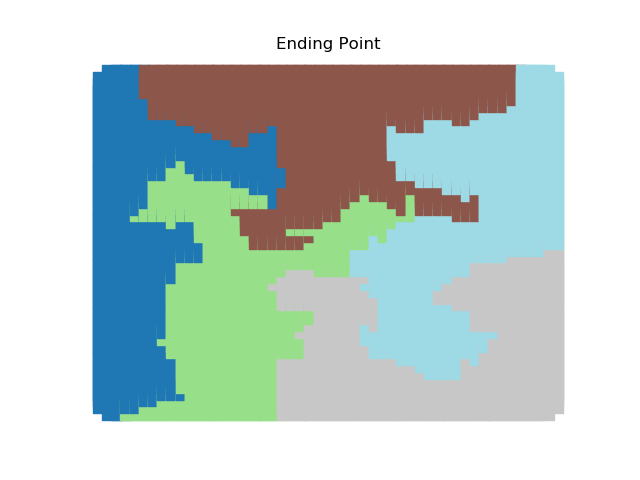
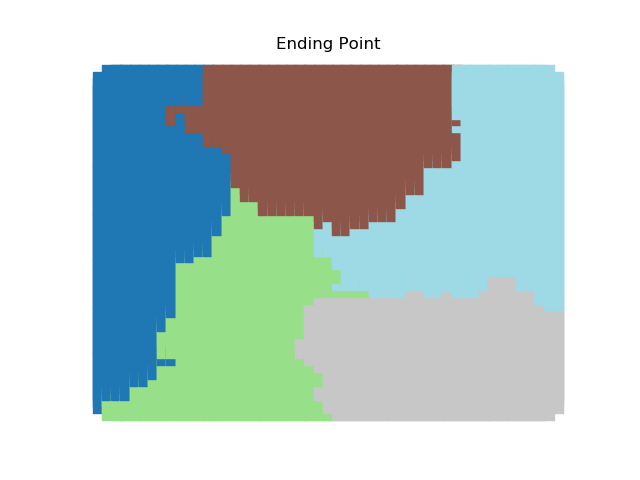
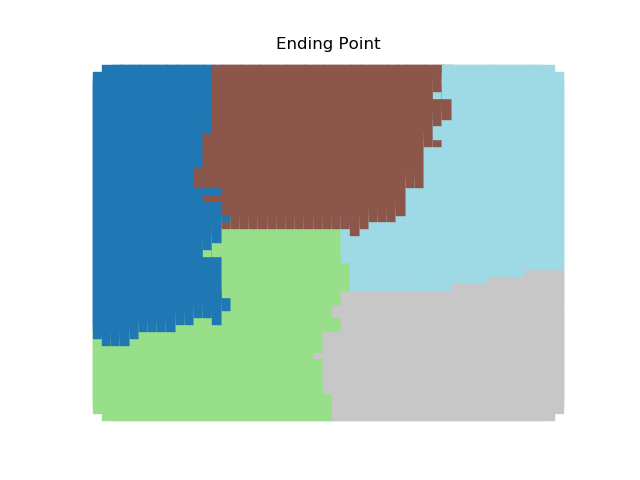
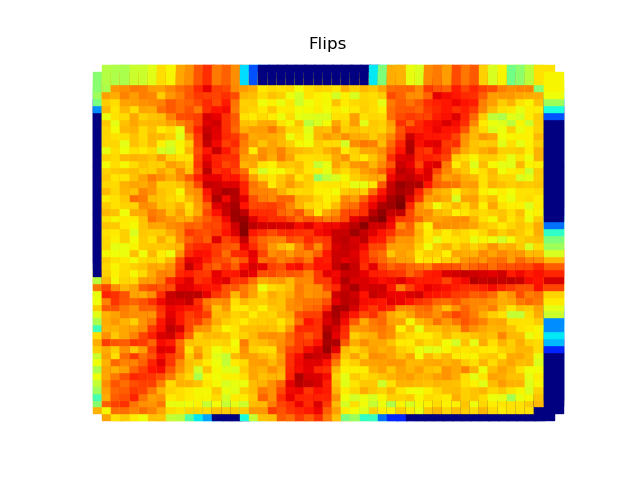
The two other grid chains use more complicated tools to generate districting plans with short boundary lengths. Both examples start by using a short (100 step) ReCom run to turn the initial vertical stripes partition into a random starting point. Then, they use a longer (10,000 step) boundary flip proposal to generate a very wiggly districting plan with lots of tentacles. To generate nicer looking final plans, the medium chain uses a spectral clustering Recom step:
| Initial Partition | Short Recom | Long Boundary | Spectral Cleanup |
|  |  |  |
| Initial Partition | Short Recom | 50k boundary steps | 100k boundary steps |
|  |  |  |
| 150 k boundary steps | 200k boundary steps | 250k boundary steps | 300k boundary steps |
 |  |  |  |
| 400 k boundary steps | 500k boundary steps | Flipped Nodes | Boundary length |
 |  |  |  |
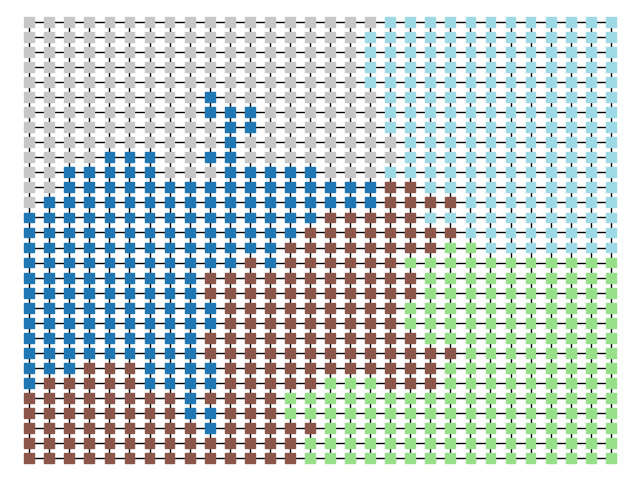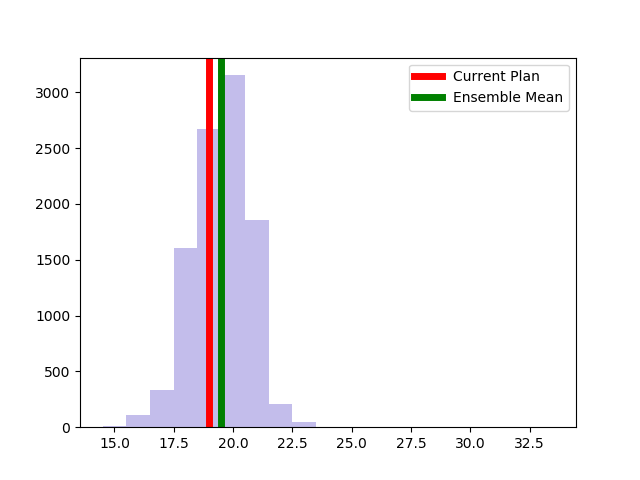
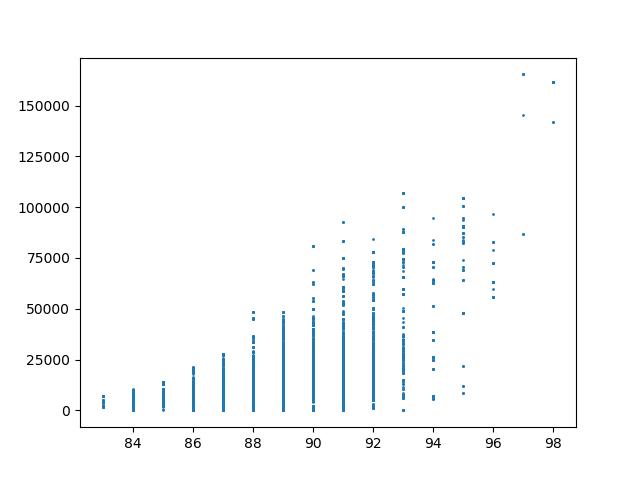
The Alaksa chain reproduces some of the experiments that were carried out in this paper. It begins by constructing a dual graph for the state directly from the shapefile and then adds in some extra edges to the dual graph to connect some islands and deletes some spurious edges that cross the water around Anchorage. The chain run itself is a pretty standard ReCom setup with a population constraint and a boundary length constraint. The only additional feature here is that at each step of the chain, the FKT algortithm is used to enumerate the number of perfect matchings of the current plat (i.e. the number of possible Senate pairings). After the run finishes, it provides box plots and seats histograms for four different election data sets as well as the proportion of Native populations in each district. These plots are automatically written to file with some summary values and .json files containing the underlying data.
| Democratic % | House Seats | Competitive Districts | Number of Matchings |
 |  |  |  |
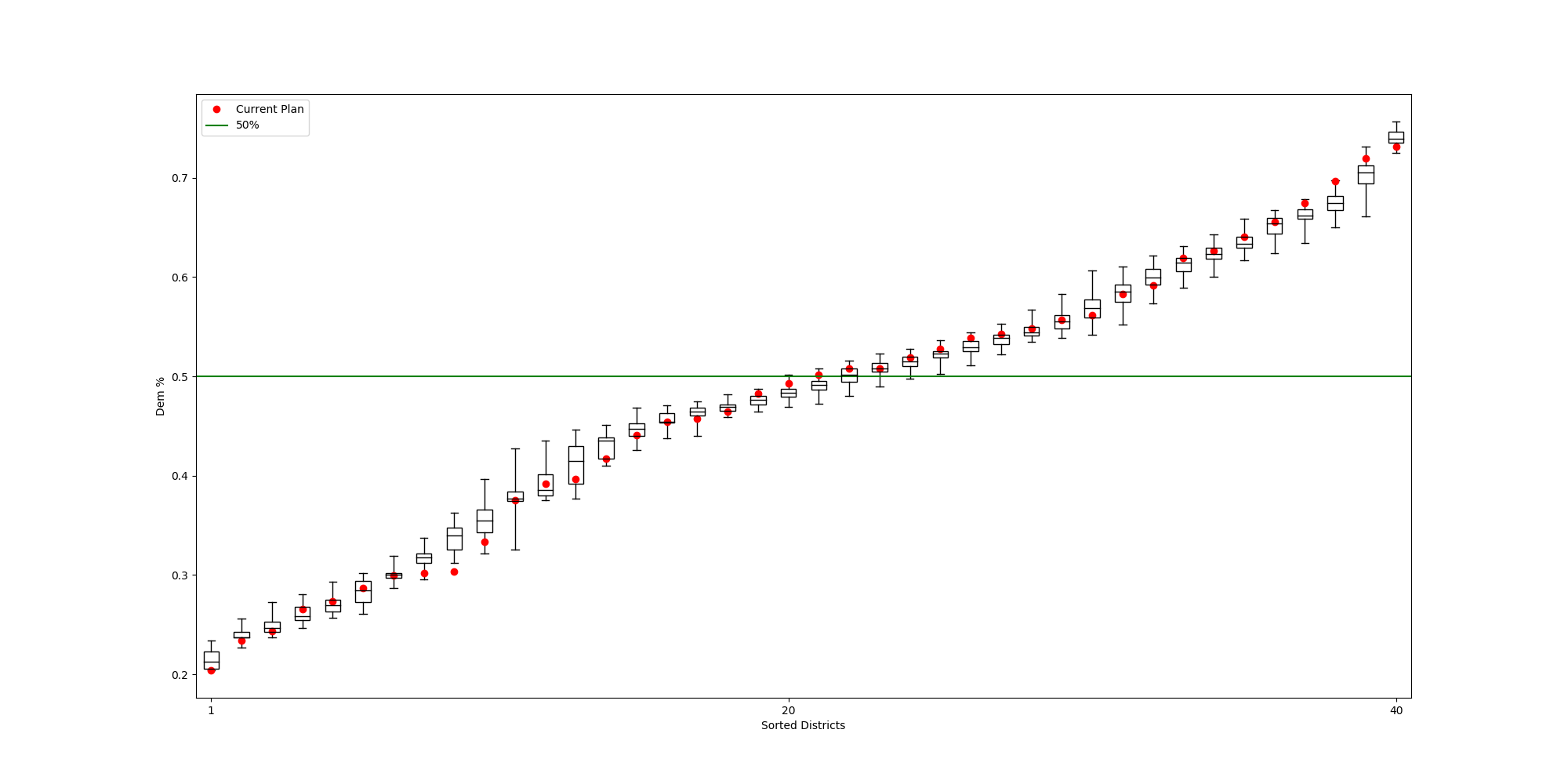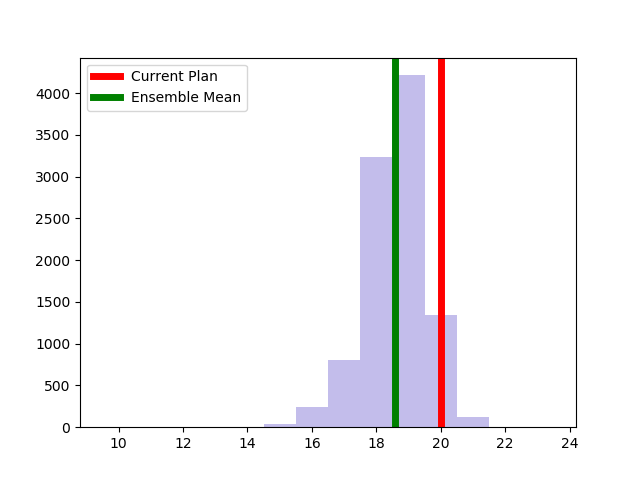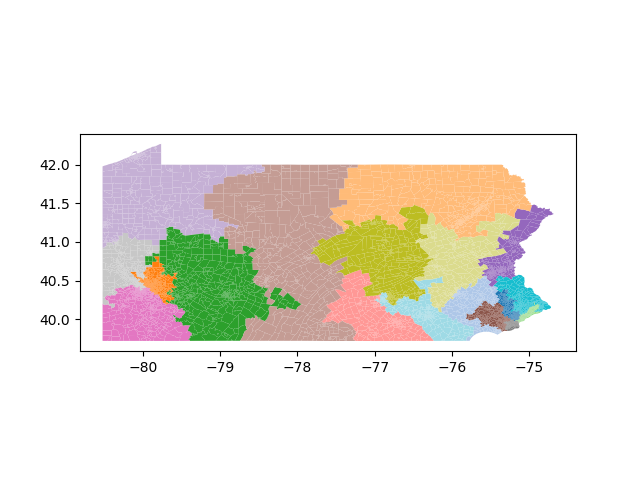
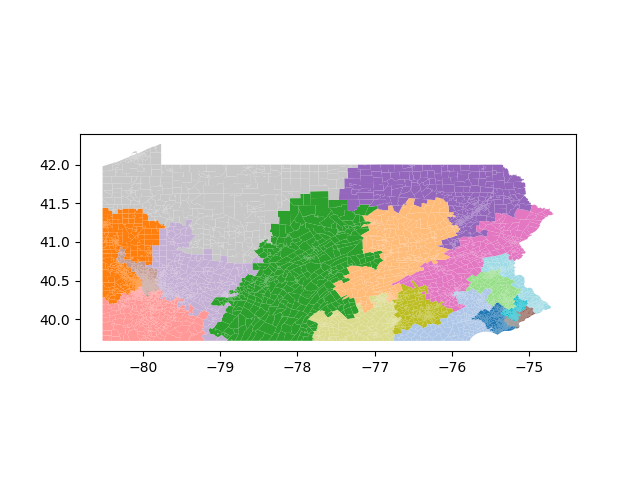
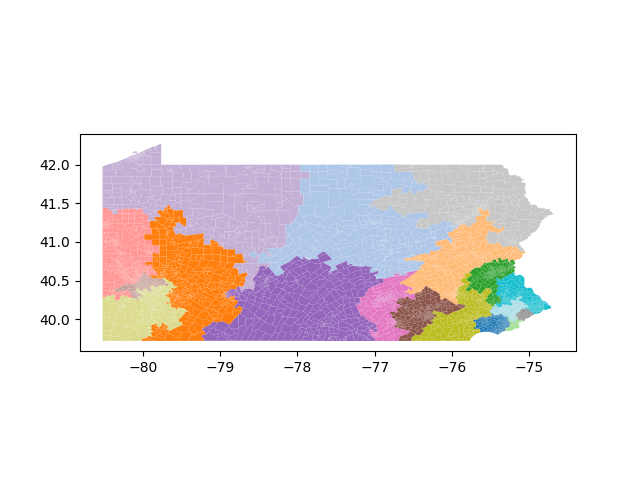
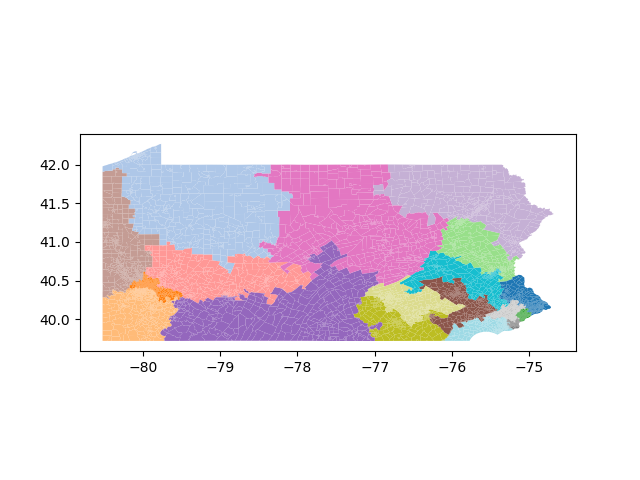
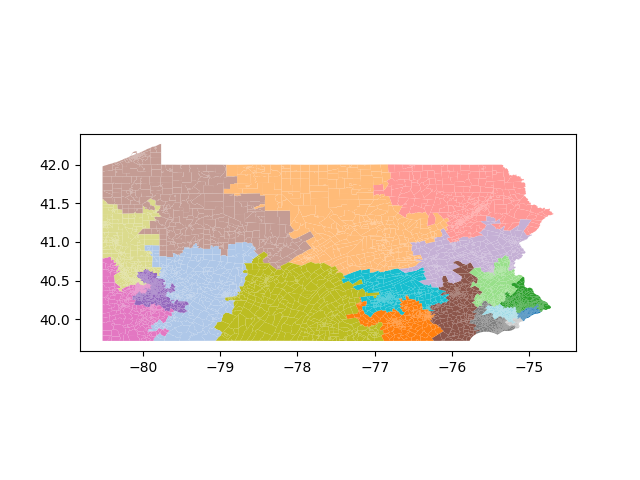
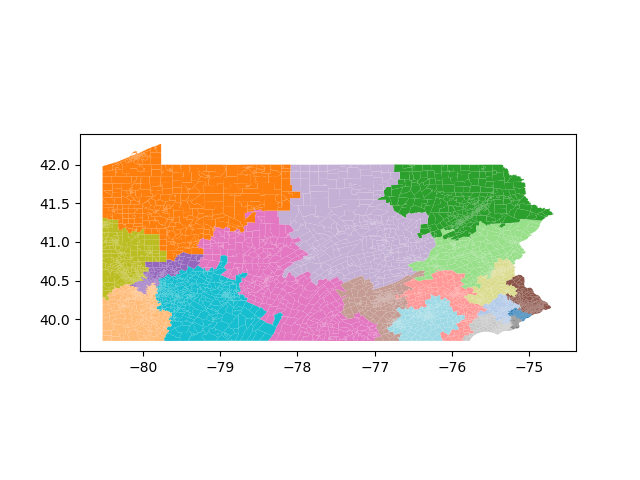
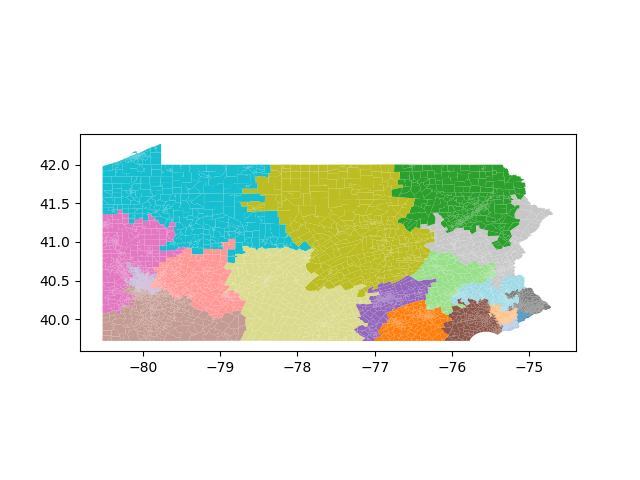
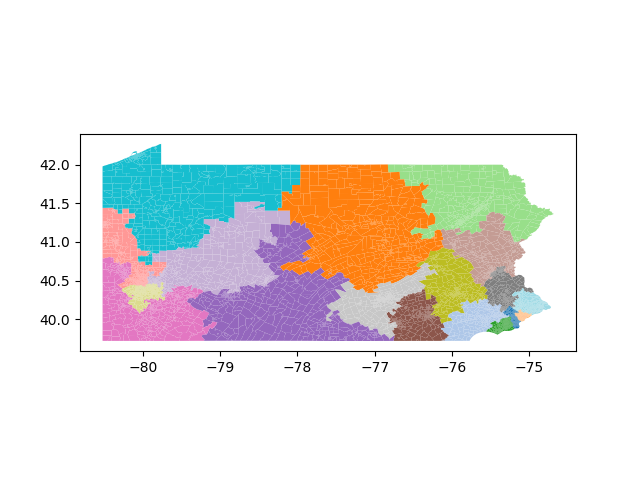
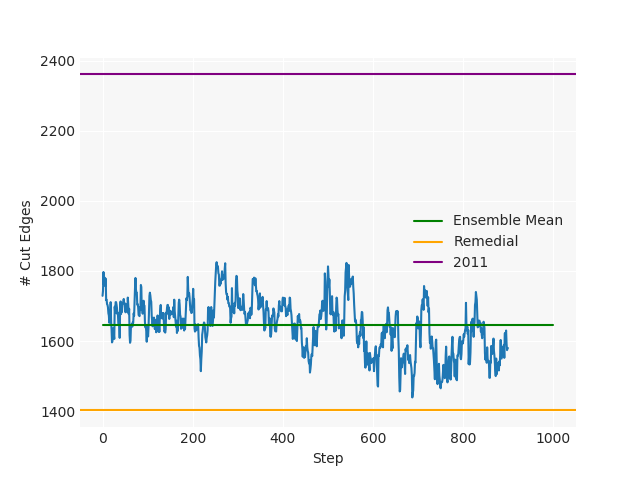
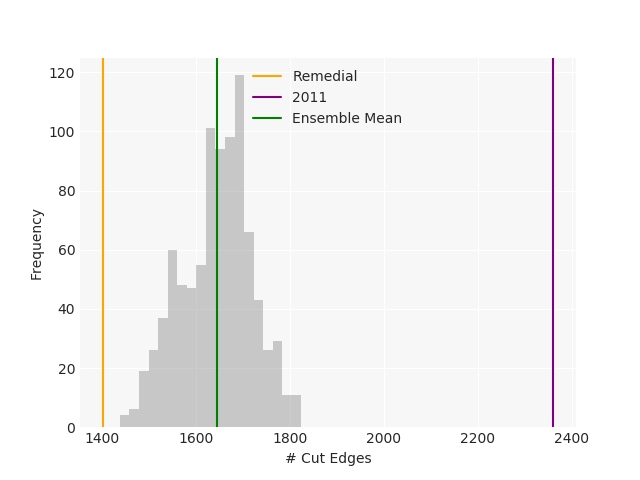
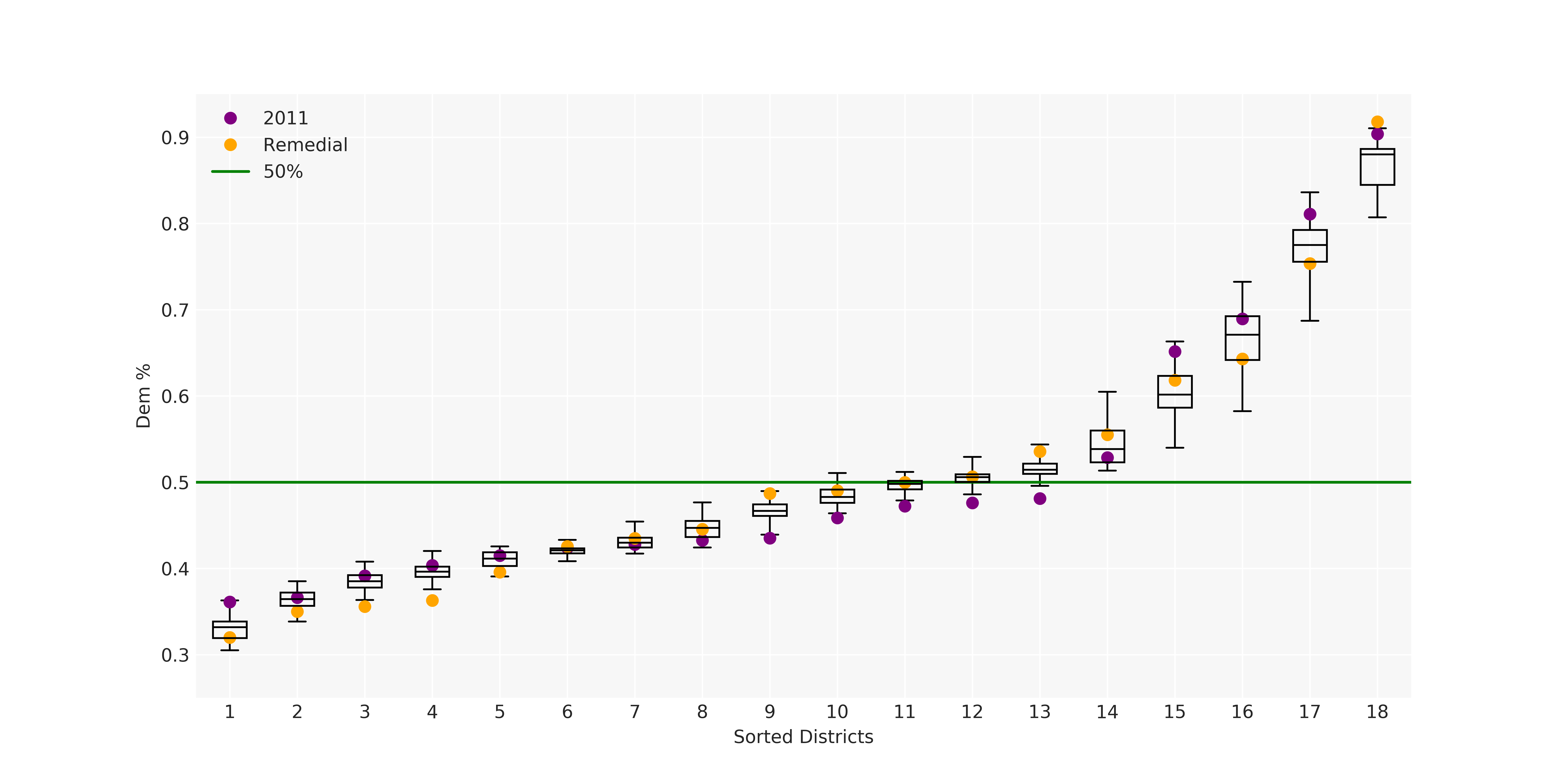
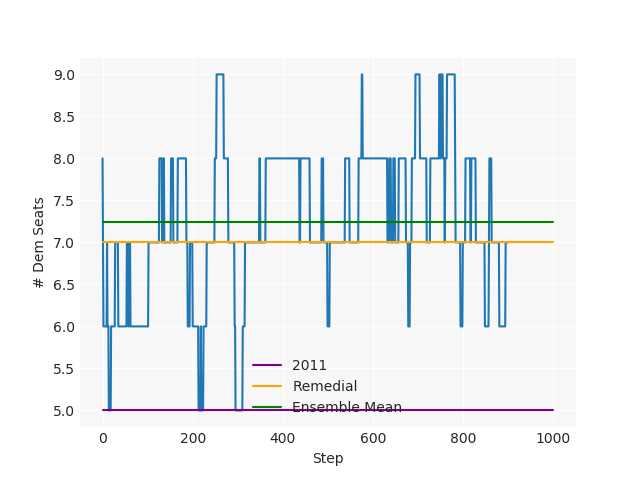
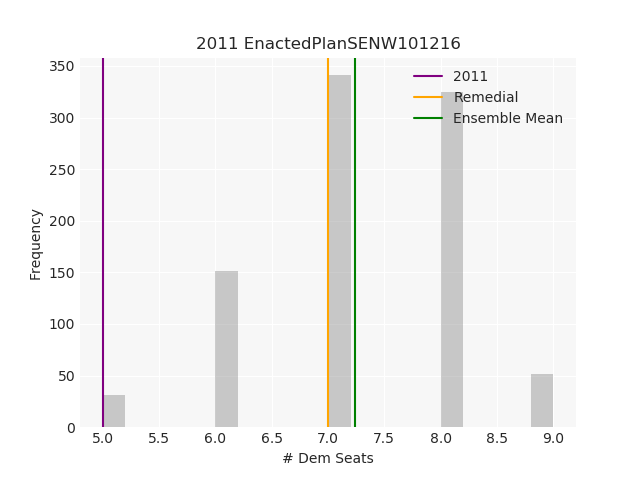
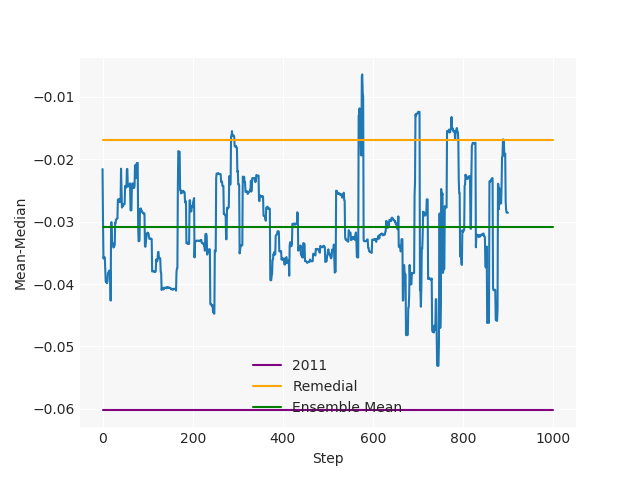
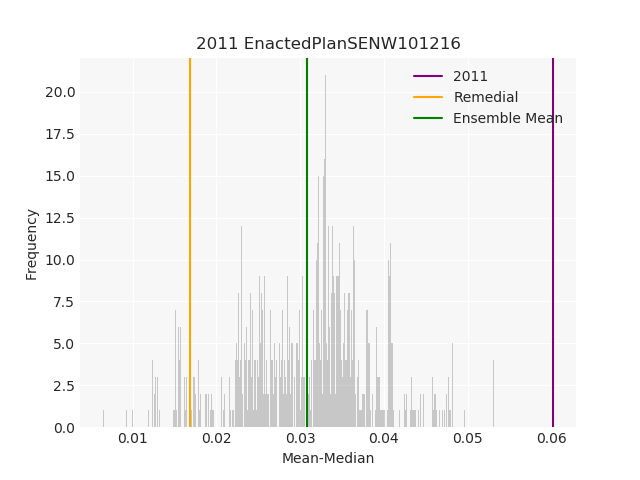
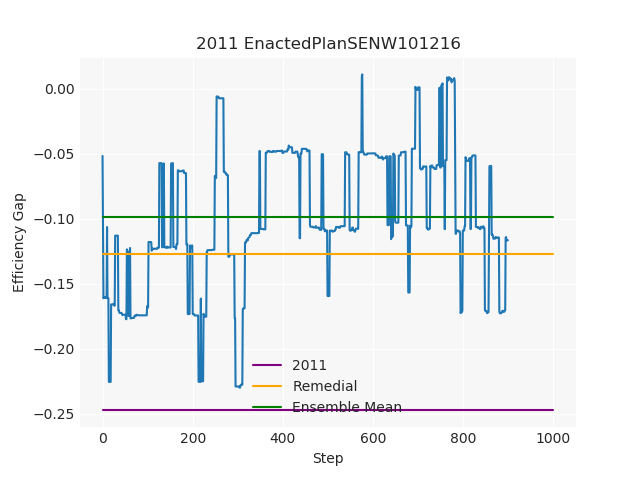
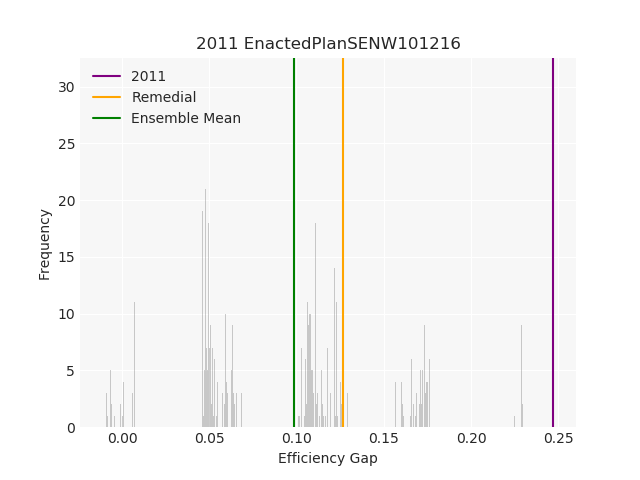
The Pennsylvania example explores a different approach to data processing. Here the dual graph is built directly from a .json file and no modifications are needed to make it contiguous. We start with the plan that was enacted in 2011 and take 1,000 ReCom steps while recording partisan statistics for 14 different elections. Every 100 steps, these values are written to file, along with a lot of the current plan. Once the chain has finished, the additional python file in the directory reads in the various outputs and creates box plots, traces, and histograms for each of the elections, as well as the boundary length, number of county splits, and population deviation. We have found this approach very useful for long runs, say 1,000,000 steps writing to file every 10,000 or so seems to keep the overhead RAM usage in a reasonable range.
| Snapshot 1 | Snapshot 2 | Snapshot 3 | Snapshot 4 |
 |  |  |
 |
| Snapshot 5 | Snapshot 6 | Snapshot 7 | Snapshot 8 |
 | |  |
|
| Snapshot 9 | Snapshot 10 | Boundary Trace | Boundary Histogram |
 |  |  |
 |
| Democratic % | Seats trace | Seats histogram | |
 |  |  | |
| Mean Median trace | Mean Median histogram | Efficiency Gap trace | Efficiency Gap histogram |
 |  |  |  |