Evaluation and Reporting Framework for Time Series Forecasting
Check Examples ~
Explore the docs »
Krisi is a Scoring library for Time-Series Forecasting. It calculates, stores and vizualises the performance of your predictions!
Krisi is tailored to measure performance over time (metrics over time). It is from the ground-up extensible and lightweight and comes with fundamental metrics for regression, classification and residual diagnostics.
It can generate reports in:
- static PDF (with
plotly) - interactive web (HTML) (with
plotly) - pretty formatted for console (with
richandplotext) - each figure displayed or saved as an svg
- Missing Rolling window based evaluation.
→ Krisi supports evaluating metrics over time. - Most TS libraries attach reporting to modelling (eg.: Darts, Statsmodel).
→ Krisi is independent of any modeling method or library. - Extendability is tedious: only works by subclassing objects.
→ Krisi supports easy configuration of custom metrics along with an extensive library of predefined metrics. - Too many dependencies.
→ Krisi has few hard dependencies (only core libaries, eg.: sklearn and plotting libraries). - Visualisation results are too basic.
→ With Krisi you can decide to share and interactive web, a static PDF, each metric diagram displayed inline or quickly look at the ScoreCard pretty printed to the console.
The project was entirely built in python.
Prerequisites
python >= 3.8andpip
Then run:
pip install krisi
If you'd like to also use interactive plotting (html) and pdf generation then run:
pip install krisi "krisi[plotting]"
You can quickly evaluate your predictions by running:
import numpy as np
from krisi.evaluate import score
print(score(y=np.random.rand(100), predictions=np.random.rand(100)))Outputs:
Model_20230505-15094466243320 <- you can add your name here
Mean Absolute Error 0.115402
Mean Absolute Percentage Error 3.272862
Symmetric Mean Absolute Percentage Error 0.718754
Mean Squared Error 0.020945
Root Mean Squared Error 0.144723
R-squared -1.108832
Mean of the Residuals -0.002094
Standard Deviation of the Residuals 0.144781
Krisi's main object is the ScoreCard that contains predefined Metrics and which you can add further Metrics to.
import numpy as np
from krisi import score
sc = score(
y=np.random.random(1000),
predictions=np.random.random(1000),
).print()Outputs:
┏━ Result of Model_20230505-130632d68aefea on Dataset_20230505-130632d4167ca4 tested on outofsam━┓
┃ ┃
┃ Targets and Predictions Analysis ┃
┃ ╭─────────────────┬────────────────────────────────────────────────┬────────────┬────────────╮ ┃
┃ │ Series Type │ Histogram │ Types │ Indicies │ ┃
┃ ├─────────────────┼────────────────────────────────────────────────┼────────────┼────────────┤ ┃
┃ │ Targets │ ┌────────────────────────────────────────┐ │ NaNs: 0 │ Start: 0 │ ┃
┃ │ │ 75.0┤ ██ │ │ dtype: │ End: 999 │ ┃
┃ │ │ 50.0┤ ██████████████ │ │ float64 │ │ ┃
┃ │ │ 25.0┤ ██ █████████████████████████ │ │ │ │ ┃
┃ │ │ 0.0┤███████████████████████████████████ ████│ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬────────┬─────────┬┘ │ │ │ ┃
┃ │ │ -0.30 -0.14 0.02 0.18 0.34 │ │ │ ┃
┃ ├─────────────────┼────────────────────────────────────────────────┼────────────┼────────────┤ ┃
┃ │ Predictions │ ┌────────────────────────────────────────┐ │ NaNs: 0 │ Start: 0 │ ┃
┃ │ │ 68.0┤ █ ██ │ │ dtype: │ End: 999 │ ┃
┃ │ │ 45.3┤ ███████████████ │ │ float64 │ │ ┃
┃ │ │ 22.7┤ ███████████████████████ │ │ │ │ ┃
┃ │ │ 0.0┤███████████████████████████████████ █ ██│ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬────────┬─────────┬┘ │ │ │ ┃
┃ │ │ -0.29 -0.13 0.03 0.19 0.34 │ │ │ ┃
┃ ╰─────────────────┴────────────────────────────────────────────────┴────────────┴────────────╯ ┃
┃ Residual Diagnostics ┃
┃ ╭─────────────────────┬─────────────────────────────────────────────────┬────────────────────╮ ┃
┃ │ Metric Name │ Result │ Parameters │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Residuals │ 0 0.055378 │ {} │ ┃
┃ │ (residuals) │ 1 -0.077456 │ │ ┃
┃ │ │ 2 -0.102910 │ │ ┃
┃ │ │ 3 -0.088878 │ │ ┃
┃ │ │ 4 -0.137035 │ │ ┃
┃ │ │ ... │ │ ┃
┃ │ │ 995 0.153345 │ │ ┃
┃ │ │ 996 0.222105 │ │ ┃
┃ │ │ 997 0.022042 │ │ ┃
┃ │ │ 998 0.013997 │ │ ┃
┃ │ │ 999 0.068374 │ │ ┃
┃ │ │ Length: 1000, dtype: float64 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Ljung Box │ lb_stat lb_pvalue │ {} │ ┃
┃ │ Statistics │ 1 0.410131 0.521903 │ │ ┃
┃ │ (ljung_box_statist… │ 2 0.411774 0.813925 │ │ ┃
┃ │ │ 3 0.541798 0.909617 │ │ ┃
┃ │ │ 4 4.200716 0.379523 │ │ ┃
┃ │ │ 5 4.217347 0.518566 │ │ ┃
┃ │ │ 6 5.934770 0.430537 │ │ ┃
┃ │ │ 7 9.905078 0.194017 │ │ ┃
┃ │ │ 8 10.020619 0.263582 │ │ ┃
┃ │ │ 9 11.102783 0.268729 │ │ ┃
┃ │ │ 10 11.268537 0.336983 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Mean of the │ -0.002 │ {} │ ┃
┃ │ Residuals │ │ │ ┃
┃ │ (residuals_mean) │ │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Standard Deviation │ 0.145 │ {} │ ┃
┃ │ of the Residuals │ │ │ ┃
┃ │ (residuals_std) │ │ │ ┃
┃ ╰─────────────────────┴─────────────────────────────────────────────────┴────────────────────╯ ┃
┃ Forecast Errors - Regression ┃
┃ ╭─────────────────────┬─────────────────────────────────────────────────┬────────────────────╮ ┃
┃ │ Mean Absolute Error │ 0.117 │ {} │ ┃
┃ │ (mae) │ │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Mean Absolute │ 7.322 │ {} │ ┃
┃ │ Percentage Error │ │ │ ┃
┃ │ (mape) │ │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Symmetric Mean │ 0.727 │ {} │ ┃
┃ │ Absolute Percentage │ │ │ ┃
┃ │ Error (smape) │ │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Mean Squared Error │ 0.021 │ {'squared': True} │ ┃
┃ │ (mse) │ │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Root Mean Squared │ 0.145 │ {'squared': False} │ ┃
┃ │ Error (rmse) │ │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Root Mean Squared │ 'Mean Squared Logarithmic Error cannot be used │ {'squared': False} │ ┃
┃ │ Log Error (rmsle) │ when targets contain negative values.' │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ R-squared (r_two) │ -0.982 │ {} │ ┃
┃ ╰─────────────────────┴─────────────────────────────────────────────────┴────────────────────╯ ┃
┃ ┃
┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛
Evaluating Metrics over time (on a rolling basis).
import numpy as np
from krisi import score
score(
y=np.random.rand(10000),
predictions=np.random.rand(10000),
calculation="rolling",
).print()Outputs:
┏━ Result of Model_20230505-1303447c37e983 on Dataset_20230505-130344cea0de16 tested on outofsam━┓
┃ ┃
┃ Targets and Predictions Analysis ┃
┃ ╭─────────────────┬────────────────────────────────────────────────┬────────────┬────────────╮ ┃
┃ │ Series Type │ Histogram │ Types │ Indicies │ ┃
┃ ├─────────────────┼────────────────────────────────────────────────┼────────────┼────────────┤ ┃
┃ │ Targets │ ┌────────────────────────────────────────┐ │ NaNs: 0 │ Start: 0 │ ┃
┃ │ │ 14.0┤ ██ │ │ dtype: │ End: 249 │ ┃
┃ │ │ 11.7┤ ██ █ │ │ float64 │ │ ┃
┃ │ │ 9.3┤ ████ ██ █ ██ ██ │ │ │ │ ┃
┃ │ │ 7.0┤██ ████████████ █ █ ███████ ██ ██ ████ │ │ │ │ ┃
┃ │ │ 4.7┤███████████████████ ████████████████████│ │ │ │ ┃
┃ │ │ 2.3┤████████████████████████████████████████│ │ │ │ ┃
┃ │ │ 0.0┤████████████████████████████████████████│ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬────────┬─────────┬┘ │ │ │ ┃
┃ │ │ -0.00 0.25 0.50 0.75 1.00 │ │ │ ┃
┃ ├─────────────────┼────────────────────────────────────────────────┼────────────┼────────────┤ ┃
┃ │ Predictions │ ┌────────────────────────────────────────┐ │ NaNs: 0 │ Start: 0 │ ┃
┃ │ │ 11.0┤ ██ │ │ dtype: │ End: 249 │ ┃
┃ │ │ 9.2┤ ███ ██ █ █ ██│ │ float64 │ │ ┃
┃ │ │ 7.3┤ ██ ██████████ ████ █ ██ ███ ████│ │ │ │ ┃
┃ │ │ 5.5┤ ██████████████ ████ █████████████████│ │ │ │ ┃
┃ │ │ 3.7┤█████████████████ ████ █████████████████│ │ │ │ ┃
┃ │ │ 1.8┤████████████████████████████████████████│ │ │ │ ┃
┃ │ │ 0.0┤████████████████████████████████████████│ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬────────┬─────────┬┘ │ │ │ ┃
┃ │ │ -0.01 0.25 0.50 0.76 1.01 │ │ │ ┃
┃ ╰─────────────────┴────────────────────────────────────────────────┴────────────┴────────────╯ ┃
┃ Residual Diagnostics ┃
┃ ╭─────────────────────┬─────────────────────────────────────────────────┬────────────────────╮ ┃
┃ │ Metric Name │ Result │ Parameters │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Residuals │ 0 -0.224918 │ {} │ ┃
┃ │ (residuals) │ 1 0.250975 │ │ ┃
┃ │ │ 2 0.206893 │ │ ┃
┃ │ │ 3 0.632068 │ │ ┃
┃ │ │ 4 0.467366 │ │ ┃
┃ │ │ ... │ │ ┃
┃ │ │ 245 0.336682 │ │ ┃
┃ │ │ 246 0.132184 │ │ ┃
┃ │ │ 247 -0.339346 │ │ ┃
┃ │ │ 248 0.422431 │ │ ┃
┃ │ │ 249 -0.424224 │ │ ┃
┃ │ │ Length: 250, dtype: float64 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Ljung Box │ 'zero-size array to reduction operation maximum │ {} │ ┃
┃ │ Statistics │ which has no identity' │ │ ┃
┃ │ (ljung_box_statist… │ │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Mean of the │ ┌────────────────────────────────────────┐ │ {} │ ┃
┃ │ Residuals │ 0.73┤ ▐ ▗ │ │ │ ┃
┃ │ (residuals_mean) │ 0.51┤▐▗▌ ▐ ▖ ▗▌ ▗ ▖ █ │ │ │ ┃
┃ │ │ 0.28┤▐▐▌▗▌▟▗▟▚▗▐▚▄▌▗▐▐▙▗▞▟ ▄▌ █ ▗ ▟▗▟▌▌▙ ▄▜ ▖│ │ │ ┃
┃ │ │ 0.05┤█▐▙▐▙█▟▐▝█▌ █▌▟▜▟▛█▌█▟█▙▌█▌█▐▐▐▌▜██▐▐▐▌▙│ │ │ ┃
┃ │ │ -0.18┤█▐█▌███▐ ▜▌ ▝▜▜ █▘█▌█▜▝█▙▛███ ▘▌▐█▜▐▐▐▐▌│ │ │ ┃
┃ │ │ -0.41┤ ▘ ▘█▜▜▝ ▐▌ ▌ ▌▘▝ █▜▌▜▌█ ▌▝▛▝█▐▐ ▘│ │ │ ┃
┃ │ │ -0.63┤ ▜ ▘ ▌ ▘ ▝ ▘ ▘▝ ▌ ▝▝▐ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬────────┬─────────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Standard Deviation │ ┌─────────────────────────────────────────┐ │ {} │ ┃
┃ │ of the Residuals │ 0.70┤ ▖▌ ▖ ▖ │ │ │ ┃
┃ │ (residuals_std) │ 0.58┤ ▗ ▌▌ ▗▌ ▖ ▖ █ ▖ ▌ ▟ ▗▗ │ │ │ ┃
┃ │ │ 0.47┤ ▐▗ ▌▌▗█▌ ▌ ▐▌ ▗ ▖█ ▐▙ ▌ ▖█ ▐▐ │ │ │ ┃
┃ │ │ 0.35┤ ▐▐▗ ▌▌▞█▙▗▌ ▗▚▐▌ ▐▗▖▌█ ▟▐ ▌▐▌█ ▗▐▐▌▖▗▌▞│ │ │ ┃
┃ │ │ 0.23┤ ▟▐█▌▖▌▙▌██▌▙▖▐▐▟▌ ▟█▌▌█▟█▝▟▌▐▐▜▙▜▛▌▜▌▐▌▌│ │ │ ┃
┃ │ │ 0.12┤▐▐▟█▜▚▌▌▌▛▛▌▜▐▐▝▛▌▟██▚▙▛█▌ ▀▌█▐▐▜▐▌ ▀█▌▌│ │ │ ┃
┃ │ │ 0.00┤▟ ▘▀ ▝▌▘▘▌▘ ▘ ▐▜▝▘ ▘ ▝ ▝ ▐▝ ▘ ▜▝▘│ │ │ ┃
┃ │ │ └┬─────────┬─────────┬─────────┬─────────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ╰─────────────────────┴─────────────────────────────────────────────────┴────────────────────╯ ┃
┃ Forecast Errors - Regression ┃
┃ ╭─────────────────────┬─────────────────────────────────────────────────┬────────────────────╮ ┃
┃ │ Mean Absolute Error │ ┌─────────────────────────────────────────┐ │ {} │ ┃
┃ │ (mae) │ 0.73┤ ▗▌▖ ▖ │ │ │ ┃
┃ │ │ 0.61┤▗ ▟▐▌▌ ▗▌ ▗ ▗ ▛▖ ▌▖ ▗▌ ▗▗ ▗█ │ │ │ ┃
┃ │ │ 0.49┤▐▐▖ █▐▌▌ ▟▌ ▌ ▐▜▐▗ ▖▌▌▞▌▐█▌ █▌▄▐▐▟██ │ │ │ ┃
┃ │ │ 0.38┤▐▟█▄█▐▐▙▟█▚▙▌▗ ▄▐▐▐▐ ▖▌▌▌▌▜██▙▌███▐▐█▛▛▖▞│ │ │ ┃
┃ │ │ 0.26┤▟▝▜▐▜▌▐▌▘█▐▌▚█▐▝▀▐▐▞▜▌▙▌█▌▝██▜▐▜▐▜▀▀▜▌ █▌│ │ │ ┃
┃ │ │ 0.14┤ ▐ ▘ ▘ █ ▘ ▜▐ ▐█ ▐█▝▌█▘ ▐ ▐▐▐ ▘ █ │ │ │ ┃
┃ │ │ 0.02┤ ▝ ▌ ▀ ▝▜ ▝ ▝ ▝ ▝ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬─────────┬─────────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Mean Absolute │ ┌─────────────────────────────────────────┐ │ {} │ ┃
┃ │ Percentage Error │ 38.2┤ ▗▌ │ │ │ ┃
┃ │ (mape) │ 31.8┤ ▐▌ │ │ │ ┃
┃ │ │ 25.5┤ ▟▟ ▐▌ │ │ │ ┃
┃ │ │ 19.1┤ ██ ▖ ▐▌ │ │ │ ┃
┃ │ │ 12.7┤ ██ ▐▌ ▌ ▐▌ │ │ │ ┃
┃ │ │ 6.4┤ ▗██ ▐▌ ▌ ▗ ▗ ▐▌ ▖ ▖ │ │ │ ┃
┃ │ │ 0.0┤▄▟▄▀▛▛▞█▙▄▙▄▄▄▄▄▟▚▟▟▟▄▚▙█▛▄▙█▚▟▟▚▟▄▟▜▞▞▄▞│ │ │ ┃
┃ │ │ └┬─────────┬─────────┬─────────┬─────────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Symmetric Mean │ ┌─────────────────────────────────────────┐ │ {} │ ┃
┃ │ Absolute Percentage │ 0.90┤ ▟▗▌ │ │ │ ┃
┃ │ Error (smape) │ 0.75┤ █▐▌▌ ▖ ▐ ▟ ▗▌ ▗ │ │ │ ┃
┃ │ │ 0.60┤▗▐ █▌▌▌▄▗▌▖ ▗▗▐▗█ █ ▖ █▌▟▟▄ ▐ ▙ ▗│ │ │ ┃
┃ │ │ 0.46┤▐▐▙▜█▌▐█▛▟▌▌▖ ▟▐▜▐▐█ ▌▛▄█▌▌█▌███▙▐▐▐▟▛▖▌│ │ │ ┃
┃ │ │ 0.31┤▐▜█▝█▌ ▀ █▚▙▙▗▐▝▘▐▐▌▐█▌▌█▌▝███▐██▜▐▞█▌▘▛▌│ │ │ ┃
┃ │ │ 0.16┤▟ ▝ ▌▘ ▛ ▘▀▛▟ ▐█▌▐█▝▌█▌ ▝▜▜▐▐▝ ▘▘▜▌ ▘ │ │ │ ┃
┃ │ │ 0.02┤ ▌ ▝▝ ▝ ▝ ▝ ▝ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬─────────┬─────────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Mean Squared Error │ ┌────────────────────────────────────────┐ │ {'squared': True} │ ┃
┃ │ (mse) │ 0.548┤ ▐▗▌ │ │ │ ┃
┃ │ │ 0.457┤ ▐▟▌ ▗▌ ▟ ▌ ▗ │ │ │ ┃
┃ │ │ 0.366┤ ▟▐█▌ ▟ ▙ ▖ ▐▚ ▟ █ ▐▌ ▄▄▗█ │ │ │ ┃
┃ │ │ 0.274┤▐▐▖ █▐█▌▗▌▌▗▌ ▛▖▌ ▗ ▐▐▄▜ █▟▗▐▌▙███▐█ │ │ │ ┃
┃ │ │ 0.183┤▐▟▙ █▐▜▌▐▌▌█▌▖▐ ▌▌▌▌▟▐▐▐█ ▙███▐▌████▐█ │ │ │ ┃
┃ │ │ 0.092┤▐▝▌██▞▐▝█▌█▝█▌▐▜▌▌▙██▐▟▐█ ▛███▐▙█▌▀▝▞▘▙▛│ │ │ ┃
┃ │ │ 0.000┤▀ ▜ ▘▝ ▝▌▝ ▘▐▞ ▛▌ ▀▞▝▝▛ ▝▌▝▛▛▌ █ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬────────┬─────────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Root Mean Squared │ ┌─────────────────────────────────────────┐ │ {'squared': False} │ ┃
┃ │ Error (rmse) │ 0.74┤ ▗▌▌ ▄ ▖ ▖ │ │ │ ┃
┃ │ │ 0.62┤▗ ▟▐▌▌ ▗▌ ▖ ▐▖▗ ▛▖ ▌ ▌▖ ▟▌▄▗▗▄▗█ │ │ │ ┃
┃ │ │ 0.50┤▐▐▖ █▐▌▌ ▟▌▗▌ ▖▐▐▐▗ ▖▖▌▌▞▚▐█▙▌███▐▐███ │ │ │ ┃
┃ │ │ 0.38┤▐▀█▄█▞▐▛▞█▚▛▌▟▐▚▟▐▐▐▟▌▌▌█▌▐███▌███▞▟▜▛▛▖▞│ │ │ ┃
┃ │ │ 0.26┤▟ ▜▐▀▌▐▌▘█▝▌▚▜▐▝▝▐▐▀▜▌▙▌█▌▝██▝▐▜▐▜▘ ▝▌ █▌│ │ │ ┃
┃ │ │ 0.14┤ ▐ ▘ ▛ ▐▐ ▐█ ▐█ ▘█ ▐ ▐▐▐ █ │ │ │ ┃
┃ │ │ 0.02┤ ▝ ▌ ▀ ▝▜ ▝ ▝ ▝ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬─────────┬─────────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ Root Mean Squared │ ┌────────────────────────────────────────┐ │ {'squared': False} │ ┃
┃ │ Log Error (rmsle) │ 0.533┤ ▐ ▖ │ │ │ ┃
┃ │ │ 0.447┤ ▟▐▟▌ ▗ ▖ ▖ ▐▌ ▗ ▟▗ ▗▌ ▗ ▟ │ │ │ ┃
┃ │ │ 0.361┤▐▐▖ █▐█▌ ▌▌ ▖ ▛▖▌▖ ▐▐▌█ ██▟▐▌▙▙██▐█ │ │ │ ┃
┃ │ │ 0.275┤▐▟▙▖█▞▐▜▟▌▙█▌▖▐▖▌▌▌▙█▐▐▐█ ▙███▐▌████▐▛▖▗│ │ │ ┃
┃ │ │ 0.189┤▐ ▌██▌▐ ▜▌▜▝█▌▐▜▘▌▙▀█▐▟▐█ ▛███▐▙█▌▘▜▞ ▙▌│ │ │ ┃
┃ │ │ 0.102┤▀ █ ▘▝ ▐▌ ▐▞ █▌ █▌▜▐▛ ▐▌▝█▌▘ ▛ │ │ │ ┃
┃ │ │ 0.016┤ ▝ ▝▌ ▝▘ ▀▌ ▘ ▘ ▘ ▘ │ │ │ ┃
┃ │ │ └┬─────────┬─────────┬────────┬─────────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ├─────────────────────┼─────────────────────────────────────────────────┼────────────────────┤ ┃
┃ │ R-squared (r_two) │ ┌───────────────────────────────────┐ │ {} │ ┃
┃ │ │ 1.0┤▝▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▜▛▀▀▀│ │ │ ┃
┃ │ │ -242903.5┤ ▐▌ │ │ │ ┃
┃ │ │ -485808.0┤ ▐▌ │ │ │ ┃
┃ │ │ -728712.5┤ ▐▌ │ │ │ ┃
┃ │ │ -971617.0┤ ▐▌ │ │ │ ┃
┃ │ │ -1214521.4┤ ▐▌ │ │ │ ┃
┃ │ │ -1457425.9┤ ▝▌ │ │ │ ┃
┃ │ │ └┬────────┬───────┬────────┬───────┬┘ │ │ ┃
┃ │ │ 1 32 63 94 125 │ │ ┃
┃ ╰─────────────────────┴─────────────────────────────────────────────────┴────────────────────╯ ┃
┃ ┃
┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛
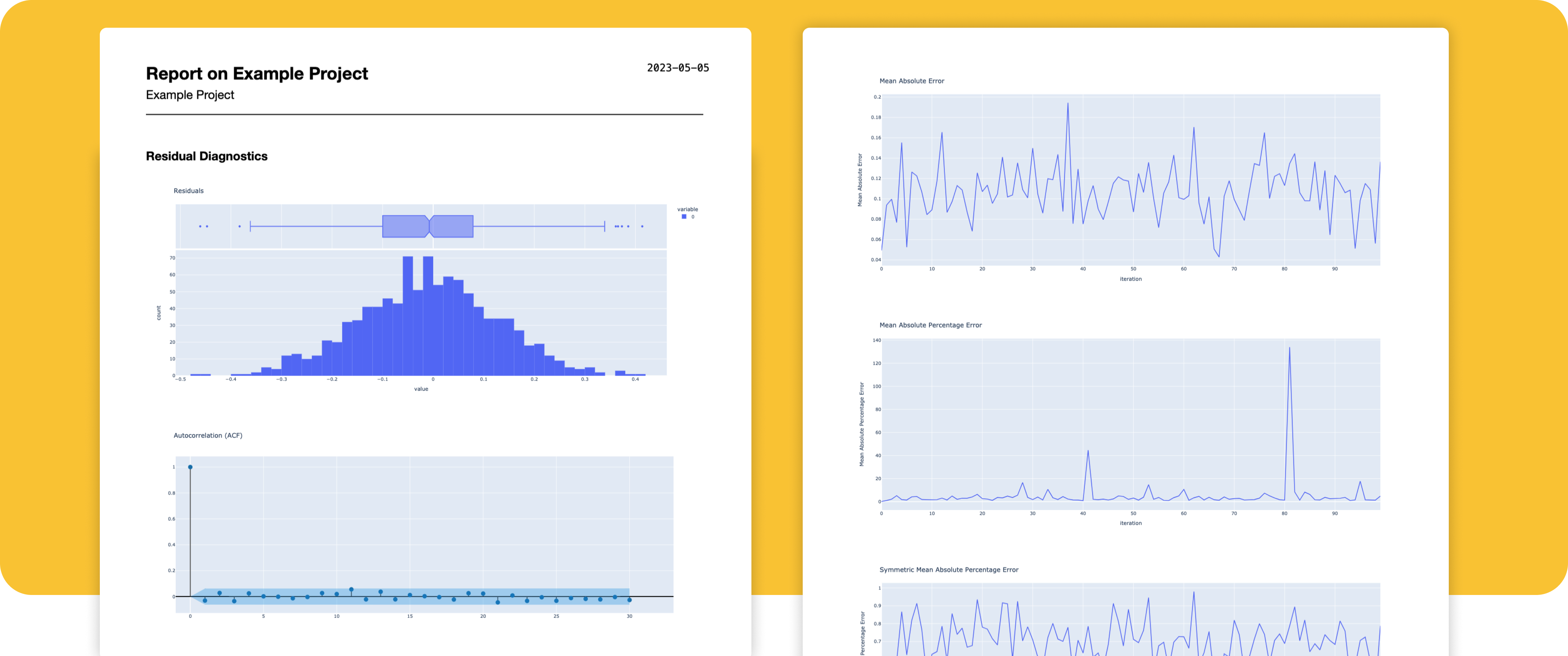
You can also show the results in a Report easily:
import numpy as np
from krisi import score
score(
y=np.random.rand(10000),
predictions=np.random.rand(10000),
calculation="rolling",
).generate_report('pdf')Generates:
See evaluate/library for source.
Contributors are continously adding new default metrics, press watch to keep track of the project and see in issues planned default metrics.
Residual Diagnostics
- Mean of the Residuals
- Standard Deviation of the Residuals
- Ljung Box Statistics
- (wip) Autocorrelation of Residuals
Regression Errors
- Mean Absolute Error
- Mean Absolute Percentage Error
- Symmetric Mean Absolute Percentage Error
- Mean Squared Error
- Root Mean Squared Error
- Root Mean Squared Log Error
- R-squared
Classification Errors
- Matthew Correlation Coefficient
- F1 Score
- Precision
- Recall
- Accuracy
| Name | Type | Dataset Type | Docs Link | Colab |
|---|---|---|---|---|
| ⚡️ Core Walkthrough | Walkthrough | Synthetic | Notebook | Colab |
| 🚄 Collapsed Metrics vs Metrics over Time | Walkthrough | Energy | - | Colab |
| 📚 Example Collection | Example | Synthetic | Collection Link | - |
If you want to try them out, we'd love to hear about your use case and help, please book a free 30-min call with us!
Creating Metrics with metadata.
import numpy as np
from krisi.evaluate import Metric, MetricCategories, ScoreCard
# Random targets and predictions for Demo
target, predictions = np.random.rand(100), np.random.rand(100)
# Create ScoreCard
sc = ScoreCard(target, predictions)
# Calculate a random metric for Demo
calculated_metric_example = (target - predictions).mean()
# Adding a simple new metric (a float)
# As a Dictionary:
sc["metric_barebones"] = calculated_metric_example
# As an Object assignment:
sc.another_metric_barebones = calculated_metric_example * 2.0
sc["metric_with_metadata"] = Metric(
name="A new, own Metric",
category=MetricCategories.residual,
result=calculated_metric_example * 3.0,
parameters={"hyper_1": 5.0},
)
# Updating the metadata of an existing metric
sc.metric_barebones = dict(info="Giving description to a metric")
# Print a pretty summary to the console
sc.print(with_info=True)Outputs:
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ Result of <your_model_name> on <your_dataset_name> tested on insample ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃ ┃
┃ Residual Diagnostics ┃
┃ ╭─────────────────────┬────────────────────────────────────────────────┬────────────────────┬─────────────────────────────────╮ ┃
┃ │ Metric Name │ Result │ Parameters │ Info │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ Mean of the │ 0.035 │ {} │ '' │ ┃
┃ │ Residuals │ │ │ │ ┃
┃ │ (residuals_mean) │ │ │ │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ Standard Deviation │ 0.42 │ {} │ '' │ ┃
┃ │ of the Residuals │ │ │ │ ┃
┃ │ (residuals_std) │ │ │ │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ A new, own Metric │ 0.105 │ {'hyper_1': 5.0} │ 'Giving description to a │ ┃
┃ │ (yet_another_metri… │ │ │ metric' │ ┃
┃ ╰─────────────────────┴────────────────────────────────────────────────┴────────────────────┴─────────────────────────────────╯ ┃
┃ Forecast Errors - Regression ┃
┃ ╭─────────────────────┬────────────────────────────────────────────────┬────────────────────┬─────────────────────────────────╮ ┃
┃ │ Mean Absolute Error │ 0.35 │ {} │ '(Mean absolute error) │ ┃
┃ │ (mae) │ │ │ represents the difference │ ┃
┃ │ │ │ │ between the original and │ ┃
┃ │ │ │ │ predicted values extracted by │ ┃
┃ │ │ │ │ averaged the absolute │ ┃
┃ │ │ │ │ difference over the data set.' │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ Mean Absolute │ 2.543 │ {} │ '' │ ┃
┃ │ Percentage Error │ │ │ │ ┃
┃ │ (mape) │ │ │ │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ Mean Squared Error │ 0.178 │ {'squared': True} │ '(Mean Squared Error) │ ┃
┃ │ (mse) │ │ │ represents the difference │ ┃
┃ │ │ │ │ between the original and │ ┃
┃ │ │ │ │ predicted values extracted by │ ┃
┃ │ │ │ │ squared the average difference │ ┃
┃ │ │ │ │ over the data set.' │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ Root Mean Squared │ 0.421 │ {'squared': False} │ '(Root Mean Squared Error) is │ ┃
┃ │ Error (rmse) │ │ │ the error rate by the square │ ┃
┃ │ │ │ │ root of Mean Squared Error.' │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ Root Mean Squared │ 0.29 │ {'squared': False} │ '' │ ┃
┃ │ Log Error (rmsle) │ │ │ │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ R-squared (r2) │ -1.28 │ {} │ '(Coefficient of determination) │ ┃
┃ │ │ │ │ represents the coefficient of │ ┃
┃ │ │ │ │ how well the values fit │ ┃
┃ │ │ │ │ compared to the original │ ┃
┃ │ │ │ │ values. The value from 0 to 1 │ ┃
┃ │ │ │ │ interpreted as percentages. The │ ┃
┃ │ │ │ │ higher the value is, the better │ ┃
┃ │ │ │ │ the model is.' │ ┃
┃ ╰─────────────────────┴────────────────────────────────────────────────┴────────────────────┴─────────────────────────────────╯ ┃
┃ Unknown ┃
┃ ╭─────────────────────┬────────────────────────────────────────────────┬────────────────────┬─────────────────────────────────╮ ┃
┃ │ own_metric │ 0.035 │ {} │ '' │ ┃
┃ │ (own_metric) │ │ │ │ ┃
┃ ├─────────────────────┼────────────────────────────────────────────────┼────────────────────┼─────────────────────────────────┤ ┃
┃ │ another_metric │ 0.07 │ {} │ '' │ ┃
┃ │ (another_metric) │ │ │ │ ┃
┃ ╰─────────────────────┴────────────────────────────────────────────────┴────────────────────┴─────────────────────────────────╯ ┃
┃ ┃
┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛
Join our Discord for live discussion!
Submit an issue or reach out to us on info at dream-faster.ai for any inquiries.